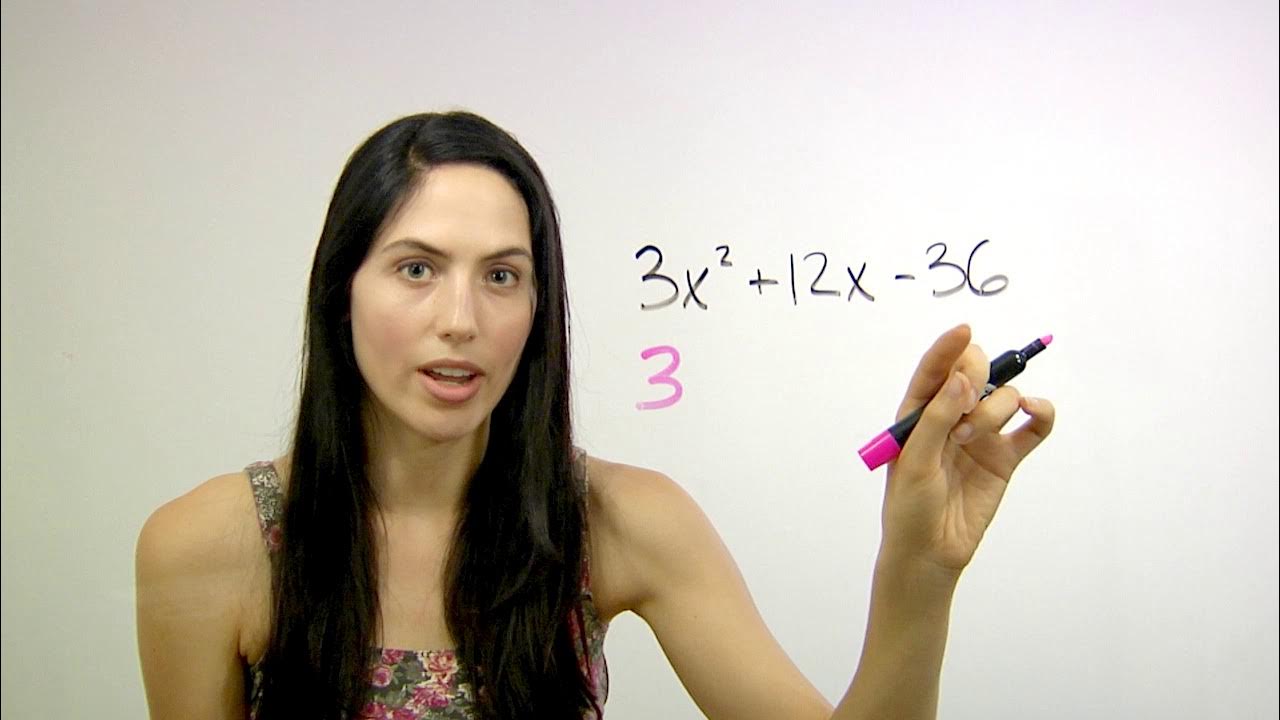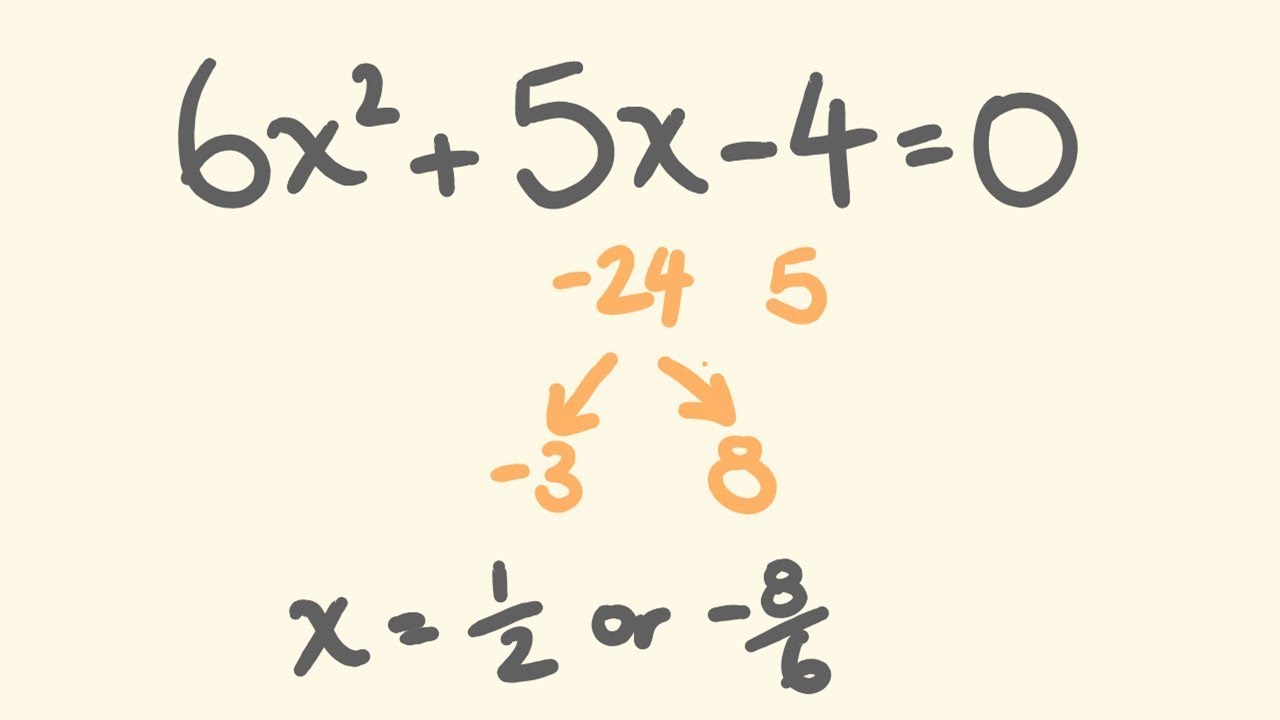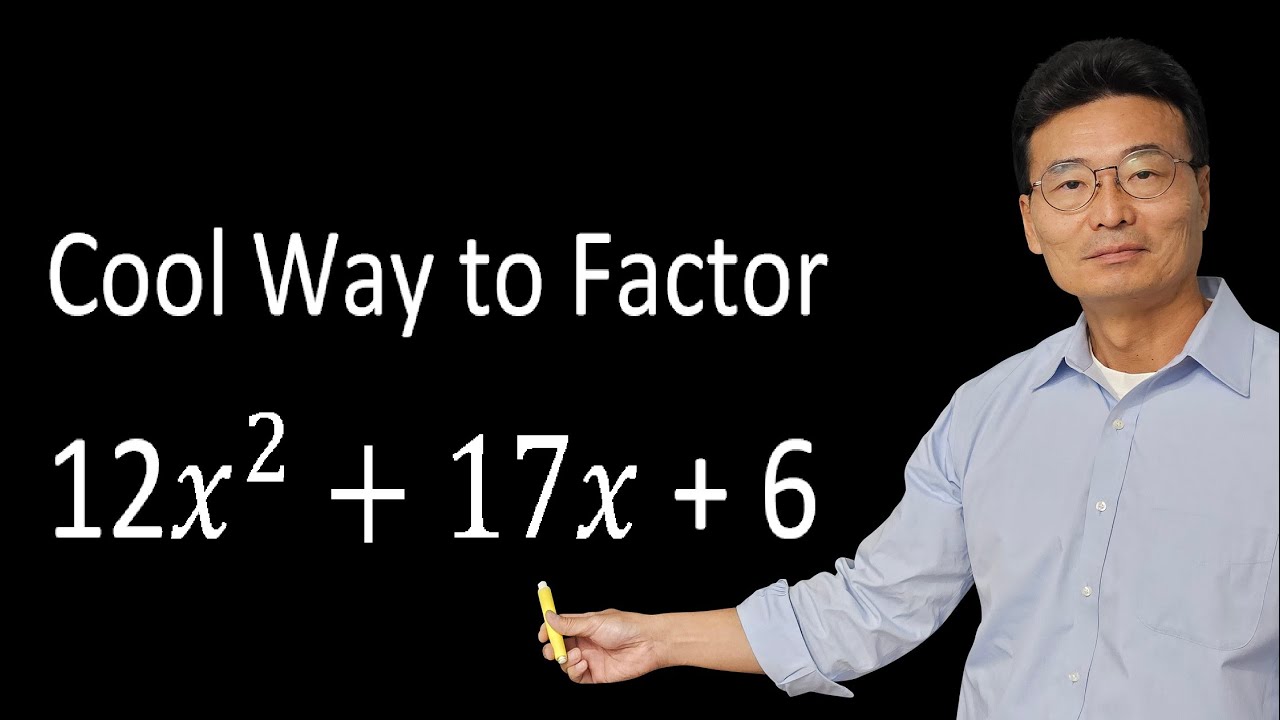How to Solve Quadratic Equations by Factoring (NancyPi)

NancyPi

15 May 201811:11

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, Nancy demonstrates how to solve quadratic equations by factoring. She begins with a simpler example, using brute force to find factors that multiply to the constant and add to the linear coefficient. Then she introduces the 'magic x' method for more complex equations, showing how to find two numbers that meet specific multiplication and addition criteria. Nancy also covers cases with a leading coefficient other than one, explaining how to factor out constants and simplify the equation. The video concludes with solving for x in both simple and complex scenarios, providing clear steps to find the solutions.

Takeaways

📚 The video is a tutorial on solving quadratic equations by factoring.
🔍 It starts with a simple example using a brute force method to find factors.
🎯 The goal is to find two numbers that multiply to the constant term and add to the linear coefficient.
📝 The script demonstrates how to list pairs of numbers that meet the multiplication and addition criteria.
✅ It shows the process of elimination to find the correct pair of numbers for factoring.
🔄 The order of factors doesn't matter as they are both in the form of 'x + number'.
✍️ After finding the factors, the next step is to set each factor equal to zero to solve for x.
🔑 The video provides an example of a quadratic equation with a leading coefficient other than 1, showing how to factor by first factoring out the common term.
🤓 For more complex equations, the 'magic x' or 'x method' is introduced as a time-saving technique.
📉 The 'x method' involves creating an X and finding two numbers that multiply to a specific product and add to a specific sum.
📌 It emphasizes the importance of dividing the found numbers by the leading coefficient for accurate factoring.
📈 The video concludes by solving the factored equations to find the solutions for x, demonstrating the effectiveness of the factoring method.

Q & A

What is the main topic of the video?
-The main topic of the video is solving quadratic equations by factoring, including the use of the 'magic x' or 'x method' for more complex equations.
What is the brute force method mentioned in the video?
-The brute force method refers to the process of finding factors by listing all possible pairs of numbers that meet certain criteria, such as multiplying to a specific number and adding to another specific number.
What are the criteria for the numbers in the brute force method of factoring quadratic equations?
-The criteria are that the two numbers must multiply to the constant term of the quadratic equation and add up to the coefficient of the linear term.
How does the video demonstrate finding the correct pair of numbers for factoring?
-The video demonstrates by listing all pairs of numbers that multiply to -16 and then checking which of those pairs add up to 6, which is the coefficient of the linear term in the example given.
What is the 'magic x' or 'x method' mentioned for solving tougher quadratic equations?
-The 'magic x' or 'x method' is a trick used to quickly find factors of a quadratic equation when the brute force method would be too time-consuming. It involves creating an 'X' and finding two numbers that multiply to the product of the first and last coefficients and add to the second coefficient.
How does the video handle quadratic equations with a leading coefficient other than 1?
-For equations with a leading coefficient other than 1, such as 2x^2, the video suggests factoring out the common number from all terms first, which simplifies the equation to a form that can be solved using the same methods as before.
What is the significance of the order of the numbers in the 'magic x' method?
-The order of the numbers in the 'magic x' method does not matter because they are used as coefficients in the factors of the quadratic equation, and the factors are symmetrical with respect to the variable x.
How does the video simplify the factors after finding the correct numbers using the 'magic x' method?
-The video suggests dividing each of the two numbers found by the leading coefficient to simplify the factors before writing them out as part of the factored quadratic equation.
What is the final step in solving a factored quadratic equation according to the video?
-The final step is to set each factor equal to zero and solve for x, which gives the solutions to the quadratic equation.
How does the video ensure that the solutions found are correct?
-The video ensures the solutions are correct by showing the process of setting each factor equal to zero and solving for x, which should yield the values that satisfy the original quadratic equation.

Outlines

00:00

📚 Introduction to Factoring Quadratic Equations

Nancy introduces the concept of solving quadratic equations by factoring. She plans to demonstrate two methods: a basic brute force method for simpler equations and a more efficient 'magic x' or 'x method' for more complex ones. The goal is to find two factors that multiply to the constant term and add up to the middle coefficient. Nancy illustrates the process with an example, guiding viewers through finding the correct pair of numbers that meet these criteria.

05:07

🔍 Factoring Quadratics with an Overall Constant

In this section, Nancy discusses how to handle quadratic equations that have an overall constant term, such as '2x^2'. She shows that by factoring out the constant, the equation can be simplified to a form that is similar to the basic examples, making it easier to solve. She emphasizes the importance of recognizing when an overall constant is present and how it can be factored out to reveal a simpler equation underneath.

10:07

🎓 Advanced Factoring with 'Magic X' Method

Nancy presents a more advanced quadratic equation starting with '3x^2' and explains the 'magic x' method for factoring. She guides the viewers through setting up an 'X' with the product of the first and last coefficients at the top and the middle coefficient at the bottom. The challenge is to find two numbers that multiply to the top number and add up to the bottom number. After identifying these numbers, they are divided by the leading coefficient to simplify the equation, leading to the factored form of the quadratic, which can then be solved by setting each factor equal to zero.

📝 Solving Factored Quadratics for Solutions

In the final paragraph, Nancy demonstrates how to solve the factored quadratic equations by setting each factor equal to zero and solving for 'x'. She provides step-by-step solutions for both factors, resulting in two solutions: 'x = 1/3' and 'x = -5'. Nancy concludes by encouraging viewers to apply these methods to save time when solving quadratic equations and invites them to interact by liking or commenting.

Mindmap

Keywords

💡Quadratic Equation

A quadratic equation is a polynomial equation of the second degree, typically in the form of ax^2 + bx + c = 0, where a, b, and c are constants, and x represents an unknown variable. In the video, quadratic equations are the main focus, and the speaker demonstrates how to solve them by factoring, which is a method of breaking down the equation into simpler components that can be more easily solved.

💡Factoring

Factoring is the process of breaking down a polynomial into a product of its factors, which are simpler polynomials. In the context of the video, factoring is used to solve quadratic equations by finding two binomials that, when multiplied together, give the original quadratic. The script illustrates this with examples, where the speaker finds pairs of numbers that satisfy the conditions of the equation.

💡Brute Force Method

The brute force method, as mentioned in the script, refers to a straightforward approach to solving a problem by trying all possible combinations or solutions until the correct one is found. In the context of factoring quadratic equations, this method involves listing all possible pairs of numbers that meet certain multiplication and addition criteria, as demonstrated in the examples provided.

💡Magic X Method

The 'magic x' method, also known as the 'x method', is a technique used to factor quadratic equations more efficiently when the brute force method would be too time-consuming. The script introduces this method as a trick to find the factors of a quadratic equation, ensuring that the factors multiply to the constant term and add up to the coefficient of the linear term.

💡Coefficients

In a quadratic equation, coefficients are the numerical factors that multiply the variables. The script refers to the leading coefficient (the factor in front of x^2) and the linear coefficient (the factor in front of x) when discussing how to factor the equation. The coefficients play a crucial role in determining the correct pairs of numbers for factoring.

💡Middle Number

The 'middle number' in the script refers to the coefficient of the linear term (bx) in a quadratic equation. This term is important when factoring because the two numbers being sought must add up to this middle number. The script uses the term to guide the process of finding the correct pairs for factoring.

💡Solving Equations

Solving equations involves finding the values of the unknown variable that make the equation true. In the video, after factoring a quadratic equation, the speaker sets each factor equal to zero to solve for x. This is a fundamental step in the process of finding the solutions to the quadratic equation.

💡Algebra Skills

Algebra skills are the methods and techniques used to manipulate and solve algebraic expressions and equations. The script mentions using algebra skills to solve for x after setting each factor equal to zero, such as adding or subtracting terms to isolate the variable.

💡Overall Constant

An overall constant in the script refers to a common factor that can be factored out from all terms of a quadratic equation, simplifying the equation before applying the factoring method. The speaker demonstrates this with an example where a 2 is factored out, revealing a simpler equation underneath.

💡Leading Coefficient

The leading coefficient is the numerical factor that multiplies the highest power of the variable in a polynomial, in this case, the a in ax^2 of a quadratic equation. The script discusses dividing the numbers found by the leading coefficient as part of the 'magic x' method to simplify the factors before solving the equation.

💡Solutions

Solutions to a quadratic equation are the values of x that satisfy the equation, making both sides equal. The script concludes with finding the solutions to the factored equations, which are the final answers to the original quadratic equation. The solutions are found by setting each factor equal to zero and solving for x.

Highlights

Introduction to solving quadratic equations by factoring.

Demonstration of a brute force method for simpler quadratic equations.

Introduction of the 'magic x' or 'x method' for more complex equations.

Explanation of finding two factors that start with x and multiply to the expression.

Guide to finding two numbers that multiply to -16 and add to 6.

Listing pairs of numbers that multiply to -16.

Identifying the correct pair of numbers that add to 6: -2 and 8.

Inserting the found numbers into the factors of the equation.

Simplification of the equation to (x - 2)(x + 8) = 0.

Setting each factor equal to zero to solve for x.

Solving for x = 2 and x = -8 using algebraic skills.

Handling quadratic equations with a leading term other than x^2.

Factoring out a common number from all terms in the equation.

Recognizing the disguised simpler equation after factoring out 2.

Using the 'magic x' method for a quadratic equation starting with 3x^2.

Finding two numbers that multiply to -15 and add to 14.

Dividing the found numbers by the leading coefficient to simplify the equation.

Writing the factored quadratic equation and solving for x = 1/3 and x = -5.

Conclusion and call to action for feedback on the demonstrated method.

Transcripts

Browse More Related Video

Factoring Quadratics... How? (NancyPi)

How to Solve By Completing the Square (NancyPi)

The Maths Prof: Factorising Quadratics (putting into double brackets)

How to Factor any Quadratic Equation Easily - Trick for factorising

Factoring Trinomials

Factoring Trinomials - Quick & Simple