Factoring Quadratics... What If You Can't? (NancyPi)
TLDRIn this educational video, Nancy addresses the common challenge of factoring quadratic expressions, particularly when they cannot be factored using traditional methods. She humorously demonstrates the process of attempting to factor a quadratic that ultimately proves unfactorable, highlighting the reality that not all quadratics can be factored. She also discusses the 'magic X' shortcut for expressions with a leading coefficient greater than one, concluding that while it can be helpful, it is not a universal solution. Nancy encourages viewers to persevere in their mathematical endeavors, even when faced with the occasional intractable problem.
Takeaways
- 🔍 Nancy discusses the common issue of factoring quadratic expressions and acknowledges that sometimes they cannot be factored.
- 📚 She mentions an example of a quadratic expression, \( x^2 - 16x + 51 \), and explains the process of finding two numbers that multiply to the constant term and add to the coefficient of the linear term.
- 🤔 Nancy admits that sometimes, despite trying, the quadratic expression may not factor, which is an important realization for students to understand.
- 👀 She suggests revisiting the 'Factoring Quadratics' introduction video for a better understanding of the process.
- 📝 Nancy lists pairs of numbers that multiply to 51 and checks which pair adds up to -16, but finds that none of them do, indicating the expression is not factorable.
- 😅 She humorously acknowledges the possibility of human error in not being able to factor a quadratic expression, emphasizing that it's okay to make mistakes.
- 🤷♀️ Nancy clarifies that if a quadratic cannot be factored, it's not due to a lack of method but rather the nature of the expression itself.
- 📉 She also addresses the topic of quadratic expressions with a leading coefficient greater than 1, such as \( 2x^2 \) or \( 3x^2 \), and how the 'magic X' method can be attempted for factoring.
- 🚫 Nancy provides a spoiler alert that the example given with a leading coefficient greater than 1 cannot be factored, reinforcing the idea that not all quadratics are factorable.
- 🔄 She explains the 'magic X' method briefly and points out that it requires finding two numbers that multiply to a specific product and add to a specific sum, which in the given example, is not possible.
- 👍 Nancy concludes by encouraging viewers to like or subscribe if they found the video helpful, showing her engagement with the audience.
Q & A
What is the main topic discussed in the video script by Nancy?
-The main topic discussed in the video script is factoring quadratic expressions and the challenges that can arise when attempting to factor them.
Why did Nancy mention the introduction video 'Factoring Quadratics'?
-Nancy mentioned the introduction video 'Factoring Quadratics' to provide additional context and guidance for viewers who may not understand the process of factoring quadratics.
What is the process of factoring a quadratic expression according to the script?
-The process involves finding two numbers that multiply to the constant term of the quadratic and add up to the coefficient of the linear term.
What is the example quadratic expression Nancy is trying to factor in the script?
-The example quadratic expression is x^2 - 16x + 51.
Why did Nancy initially struggle to factor the example quadratic expression?
-Nancy initially struggled because she could not find two numbers that met the criteria of multiplying to 51 and adding up to -16.
What does Nancy reveal about the possibility of not being able to factor a quadratic expression?
-Nancy reveals that sometimes a quadratic expression cannot be factored, and it's important to recognize when this is the case.
What is the 'magic X' shortcut method mentioned by Nancy for factoring quadratics with a leading coefficient greater than one?
-The 'magic X' shortcut method involves using the product of the leading coefficient and the constant term to find two numbers that multiply to this product and add up to the coefficient of the linear term.
Why did Nancy say that the 'magic X' shortcut method did not help in the example provided?
-The 'magic X' shortcut method did not help because there were no two numbers that could multiply to -48 and add up to 4, indicating the quadratic could not be factored.
What is the advice Nancy gives about assuming factorability when starting to work on a problem?
-Nancy advises to assume that a problem can be factored when starting to work on it because most quadratics can be factored, but to recognize when it might not be possible due to human error or the nature of the problem.
How does Nancy address the viewers' concerns about the 'magic X' method working for all quadratics?
-Nancy confirms that the 'magic X' method works for all factorable quadratics, but if a quadratic is not factorable, no method will be successful.
What is Nancy's closing remark about liking math and the video?
-Nancy humorously acknowledges that not everyone has to like math but encourages viewers to like her video if they found it helpful.
Outlines
😅 Factoring Challenges and the Reality of Unfactorable Quadratics
In this paragraph, Nancy addresses a common question about factoring quadratic expressions, specifically the example of x^2 - 16x + 51. She explains the usual method of finding two numbers that multiply to the constant term and add up to the coefficient of the linear term. However, she humorously admits that none of the pairs she lists work for this particular expression, leading to the realization that not all quadratics can be factored. Nancy emphasizes that it's important to recognize when a quadratic is unfactorable and not to get discouraged by this, attributing the difficulty to human error and the limitations of the factoring methods discussed.
🤔 The Limitations of the Magic X Method for Factoring Quadratics
Nancy continues the discussion by addressing the limitations of the 'magic X' shortcut method for factoring quadratics, especially when the leading coefficient is greater than one. She provides an example and explains the process of using the magic X method, which involves finding two numbers that multiply to a specific product and add up to another number. Despite trying, Nancy finds that the method does not work for her example, confirming that the quadratic is indeed unfactorable. She reassures viewers that encountering unfactorable expressions is a normal part of mathematical problem-solving and encourages them to understand the limitations of factoring methods.
Mindmap
Keywords
💡Factoring
💡Quadratic
💡Pairs of numbers
💡Magic X
💡Leading coefficient
💡Unfactorable
💡Human error
💡Trial and error
💡Coefficient
💡Introduction video
💡Factorable
Highlights
Introduction to the common issue of factoring quadratic expressions and the realization that not all can be factored.
Explanation of the process to find two numbers that multiply to the constant term and add to the linear coefficient in a quadratic expression.
Listing of possible number pairs that multiply to 51 to find a potential factorization for the quadratic x^2 - 16x + 51.
Demonstration of checking each pair of numbers to see if they add up to -16, revealing none do.
Admission of the inability to factor the given quadratic expression, highlighting the reality that not all quadratics are factorable.
Humor and self-deprecation used to lighten the mood about the unexpected outcome of the factoring attempt.
Emphasis on the importance of recognizing when a quadratic cannot be factored and the instructions to state so if that's the case.
Acknowledgment of human error in the factoring process and the suggestion to initially assume factorability.
Introduction of the 'magic X' shortcut method for factoring quadratics with a leading coefficient greater than 1.
Illustration of the 'magic X' method with an example that ultimately cannot be factored, debunking the myth of its universal applicability.
Explanation of the 'magic X' method steps, including finding two numbers that multiply to a specific product and add to a given sum.
Confirmation that the 'magic X' method works for factorable quadratics but not for those that are unfactorable.
Encouragement for viewers to understand that struggling with factoring is normal and not a sign of failure.
Light-hearted conclusion about the unpopularity of factoring among students, with a call to action for likes and subscriptions.
Transcripts
Browse More Related Video
Factoring Quadratics... How? (NancyPi)
How to Solve Quadratic Equations by Factoring (NancyPi)
How to Solve By Completing the Square (NancyPi)
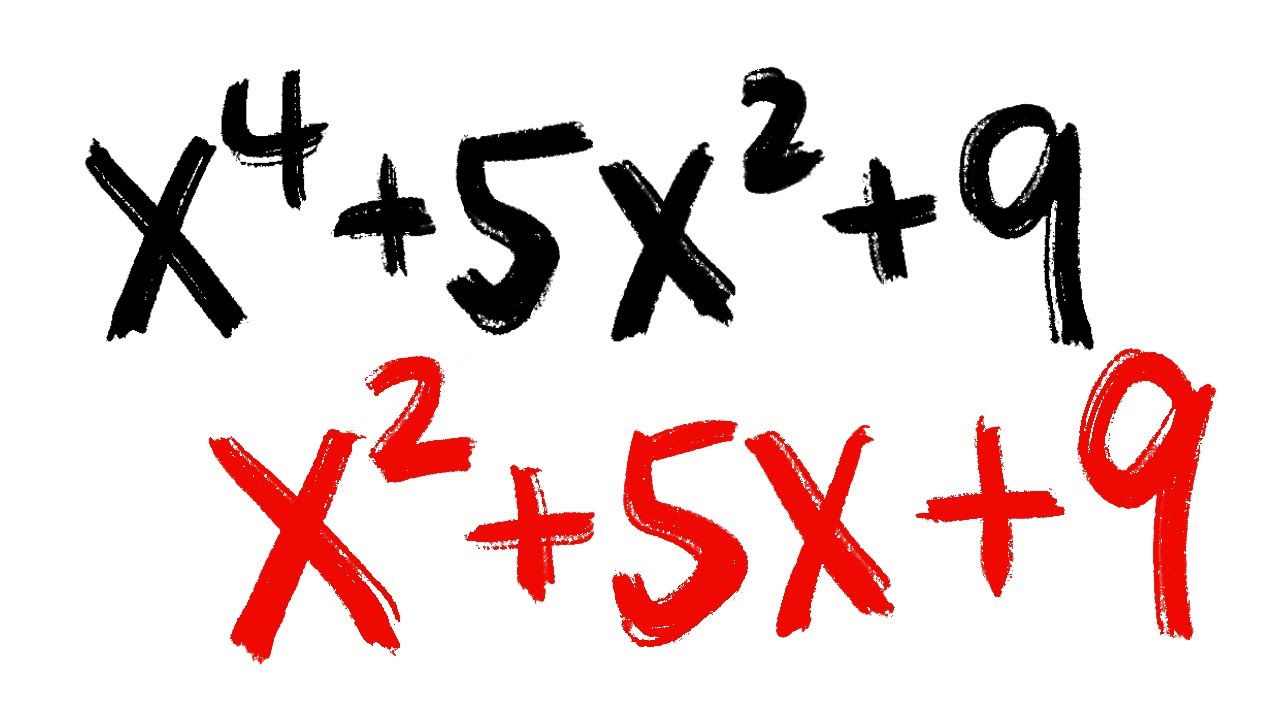
algebra tutorial: factoring a quartic trinomial vs a quadratic trinomials
Trig Substitution... How? (NancyPi)

Solving Exponential Equations with Common Bases (Precalculus - College Algebra 54)
5.0 / 5 (0 votes)
Thanks for rating: