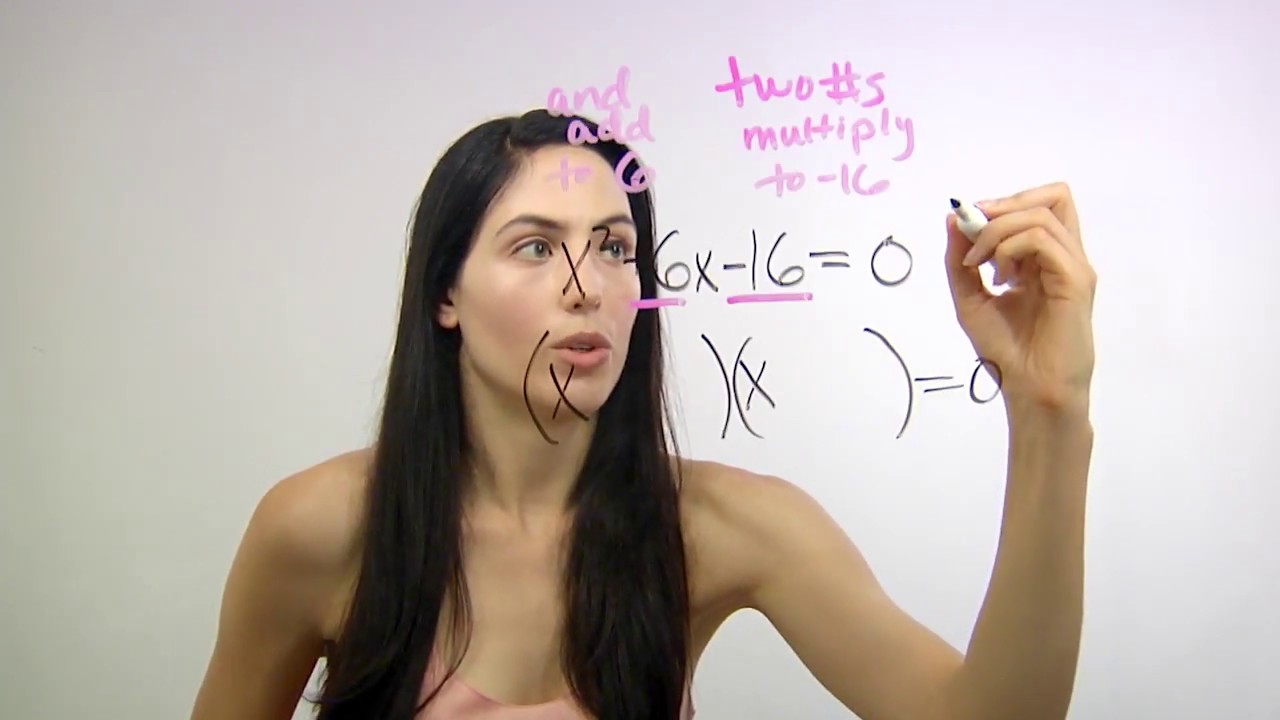Factoring Trinomials

Mr H Tutoring
8 Jul 202304:17
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script teaches a unique method for factoring trinomials with a leading coefficient other than one, a technique not commonly covered in schools. The presenter demonstrates two examples, showing how to find two numbers that multiply to the constant term and add up to the middle coefficient, then divides and simplifies the expression to reveal the factored form. The method simplifies complex algebraic expressions, making it a valuable tool for students preparing for exams.

Takeaways
  • 📚 The video explains a method for factoring trinomials with a leading coefficient that is not one, which is useful for scoring in the U.S.
  • 🔢 The first step is to multiply the leading coefficient by the constant term to form a new quadratic expression.
  • ➗ After forming the new expression, the next step is to factor it by finding two numbers that multiply to the constant term and add up to the linear coefficient.
  • 🔍 For the example given, the numbers that multiply to 72 and add up to 17 are 8 and 9.
  • 📉 The leading coefficient from the original expression is then divided by the new leading coefficient to adjust the factors.
  • ✂️ The fractions are reduced to their simplest form, resulting in the final factored form of the trinomial.
  • 📝 The second example demonstrates the method with a negative middle term, emphasizing the need to find numbers that subtract to the linear coefficient.
  • 🔄 The process involves adjusting the signs of the factors based on the sign of the middle term in the original trinomial.
  • 📈 The numbers that multiply to 24 and subtract to 5 are 8 and 3, with 8 being associated with the negative sign.
  • 📉 The leading coefficient is again divided by the new leading coefficient to simplify the factors.
  • 📚 The final step involves multiplying the denominators by the variable x and simplifying to get the factored form of the original trinomial.
  • 👍 The video encourages viewers to subscribe and support the channel, highlighting the importance of community engagement.
Q & A

  • What is the process described in the video script for factoring a trinomial with a leading coefficient that is not one?

    -The process involves first multiplying the leading coefficient by the constant term to form a new quadratic expression. Then, factor the new quadratic expression by finding two numbers that multiply to the constant term and add up to the linear coefficient. Adjust the factors accordingly and simplify the expression to get the final factored form.

  • Why is it necessary to multiply the leading coefficient by the constant term when factoring a trinomial?

    -Multiplying the leading coefficient by the constant term is a step to create a new quadratic expression that can be more easily factored by adjusting the middle term and finding two numbers that satisfy the conditions of multiplication and addition.

  • In the first example, what are the two numbers that multiply to 72 and add up to 17?

    -The two numbers that multiply to 72 and add up to 17 are 8 and 9.

  • How does the sign of the third term in a trinomial affect the factoring process?

    -The sign of the third term determines whether the factors will have the same or opposite signs. If the third term is positive, the factors will have the same sign; if negative, they will have opposite signs.

  • What is the purpose of dividing the middle terms by the leading coefficient after finding the correct pair of numbers?

    -Dividing the middle terms by the leading coefficient is done to simplify the factors and to adjust for the multiplication that was done at the beginning of the process.

  • In the second example, what are the two numbers that multiply to 24 and subtract to give 5?

    -The two numbers that multiply to 24 and subtract to give 5 are 8 and 3.

  • Why is it important to place the larger number with the negative sign when factoring a trinomial with a negative third term?

    -Placing the larger number with the negative sign ensures that the subtraction of the two numbers results in the correct linear coefficient of the original trinomial.

  • How does the script suggest multiplying the denominators to the X terms in the factored expression?

    -The script suggests multiplying the denominators to the X terms to eliminate the fractions and simplify the expression to a form that can be easily multiplied out to verify the original trinomial.

  • What is the final step in verifying the factored expression of the original trinomial?

    -The final step is to multiply the factored expression to see if it equals the original trinomial, ensuring that the factoring process was done correctly.

  • What does the script suggest for those who have not seen this method before?

    -The script suggests that this method will help those who have not seen it before to factor trinomials with a leading coefficient that is not one and encourages them to subscribe and support the channel for more such content.

  • How can one ensure that the factored form of a trinomial is correct?

    -One can ensure the factored form is correct by multiplying the factors together and checking if the result matches the original trinomial, including all terms and their coefficients.

Outlines
00:00
📚 Factoring Trinomials with Non-One Leading Coefficients

This paragraph introduces a method for factoring trinomials where the leading coefficient is not one, a technique that might not be commonly taught in schools but is useful for standardized tests in the U.S. The example given involves a trinomial (x^2 + 17x + 72). The process begins by multiplying the leading coefficient (12) by the constant term (6), resulting in the expression (x^2 + 17x + 72). The next step is to factor this expression by finding two numbers that multiply to 72 and add up to 17, which are 8 and 9. The video demonstrates how to rewrite the trinomial as (x + 8)(x + 9) and then simplify the fractions by dividing by the leading coefficient, resulting in (x + 2)/3 and (x + 3)/4. The final step involves multiplying the denominators by the respective x terms to get the factored form (3x + 2)(4x + 3).

🔍 Factoring Negative Trinomials with Non-One Leading Coefficients

The second paragraph continues the theme of factoring trinomials with a leading coefficient other than one, this time with a negative constant term. The example provided is (x^2 - 5x - 24). The process starts by multiplying the leading coefficient (6) by the constant term (-24), resulting in (x^2 - 5x - 24). The factoring process involves finding two numbers that multiply to -24 and have a difference of 5, which are 8 and -3. The video explains how to adjust the signs to account for the negative third term and places the larger number with the negative sign, resulting in (x + 3)(x - 8). The fractions are then simplified by dividing by the leading coefficient, yielding (x + 1)/2 and (x - 4)/3. The final step is to multiply the denominators by the x terms, resulting in the factored form (2x + 1)(3x - 4).

Mindmap
Keywords
💡Factoring
Factoring refers to the process of breaking down a polynomial into a product of its factors, which are simpler polynomials or constants. In the video's theme, factoring is essential for solving trinomials with leading coefficients other than one, as demonstrated through the examples provided.
💡Trinomial
A trinomial is a polynomial with three terms. The video script focuses on factoring trinomials, particularly those with leading coefficients that are not one, which requires a specific method to simplify the expression into a product of binomials.
💡Leading Coefficient
The leading coefficient is the numerical factor that multiplies the highest power of the variable in a polynomial. In the context of the video, the leading coefficient is not one, which complicates the factoring process and necessitates the method discussed.
💡Expression
In mathematics, an expression is a combination of variables, operators, and constants that can be simplified or evaluated. The script discusses transforming complex trinomial expressions into simpler factored forms.
💡Multiplying Coefficients
The process of multiplying coefficients involves taking the numerical factors of each term in a polynomial and multiplying them together. In the script, this is done to adjust the leading coefficient to one, facilitating the factoring process.
💡Factors
Factors are the components into which a polynomial can be broken down during the factoring process. The video demonstrates finding the correct pair of factors for a given trinomial that, when multiplied, yield the original polynomial.
💡Pairs of Numbers
The script refers to pairs of numbers that, when multiplied together, result in a specific product (e.g., 72). These pairs are crucial for determining the correct factors to use in the factoring of a trinomial.
💡Denominator
The denominator is the bottom part of a fraction, indicating the number of equal parts the whole is divided into. In the script, after finding the factors, the denominator is used to simplify the resulting fractions to whole numbers.
💡Simplifying Fractions
Simplifying fractions involves reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor. The script shows this process as part of the factoring method.
💡Multiplying Out
Multiplying out is the process of expanding a product of binomials back into a polynomial. In the script, this is done to verify that the factored form of the trinomial is correct by comparing it to the original expression.
💡Subscription
Although not directly related to the mathematical content, subscription is a term used in the context of the script to encourage viewers to subscribe to the channel for more educational content, indicating the video's intent to engage its audience.
Highlights

Introduction to factoring trinomials where the leading coefficient is not one.

Multiplying the leading coefficient with the constant term to simplify the expression.

Transformed expression: x^2 + 17x + 72.

Listing pairs of numbers that multiply to 72 and add up to 17.

Identifying the pair (8, 9) that adds up to 17.

Dividing by the initial leading coefficient to adjust the pairs.

Simplified fractions: x + 2/3 and x + 3/4.

Multiplying denominators to the x terms: 3x + 2 and 4x + 3.

Verifying the factored form by multiplying it back.

Starting a second example with a different trinomial.

Transforming x^2 - 5x - 24 using the same initial multiplication.

Factoring x^2 - 5x - 24 with plus and minus signs due to a negative constant term.

Listing pairs of numbers that multiply to 24 and subtract to 5.

Identifying the pair (3, 8) that subtracts to 5.

Adjusting the pair based on the negative middle term.

Simplified fractions: x + 1/2 and x - 4/3.

Multiplying denominators to the x terms: 2x + 1 and 3x - 4.

Verifying the factored form by multiplying it back.

Emphasizing the usefulness of this method for trinomials with leading coefficients not equal to one.

Transcripts

Browse More Related Video

Box Method of Factoring Trinomials (10 Examples)

Factoring Trinomials - Quick & Simple

How to Solve Quadratic Equations by Factoring (NancyPi)

Factoring Quadratics... How? (NancyPi)

Factoring Quadratic Expressions Pt. 1

Using Factoring to Solve Quadratics (Precalculus - College Algebra 18)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Trinomial FactoringMath TutorialEducationalLeading CoefficientsAlgebra TechniquesMathematicsX PlusFactoring MethodNumber PairsSubscription Call