Math 119 Chapter 4 Part 1
TLDRThis video script delves into the fundamentals of probability in statistics, focusing on the concept of rare events and their implications on assumptions. It introduces the sample space, simple events, and the three main approaches to probability: relative frequency, classical, and subjective. The script provides examples, including gender outcomes in births and NBA player statistics, to illustrate how probabilities are calculated and interpreted. The law of large numbers and the addition rule for probabilities are also discussed, with practical examples to avoid double counting in scenarios like pre-employment drug testing.
Takeaways
- 📚 The lecture introduces Chapter 4 focusing on probabilities and their role in inferential statistics.
- 🤔 The concept of 'rare event rule' is explained, stating that if the probability of an observed event is very low under a given assumption, the assumption is likely incorrect.
- 📉 The difficulty of the section is acknowledged, with an invitation for students to seek help through meetings or emails.
- 🔢 Definitions are provided, differentiating between an event, a simple event, and the sample space, with examples given for clarity.
- 👶 An example using the gender of children born to a woman is used to illustrate the concepts of sample space and simple events.
- 🎯 Three different approaches to understanding probability are discussed: relative frequency, classical, and subjective.
- 🎲 The classical approach to probability is detailed, emphasizing the need for equally likely outcomes and how to calculate probabilities in such cases.
- 🏀 The use of abbreviations in probability notation is highlighted, with examples from sports statistics, such as basketball free throw percentages.
- ☔ The subjective approach to probability is explained, using meteorologists' predictions as an example of estimating probabilities based on expert knowledge.
- 🧩 The law of large numbers is introduced, explaining how the relative frequency of an event approaches the actual probability as the number of trials increases.
- 🚫 The fundamental rule that probabilities range between 0 and 1 is reiterated, with explanations of what probabilities of 0 and 1 signify.
Q & A
What is the main topic of Chapter Four in the transcript?
-The main topic of Chapter Four is learning about probabilities, which are used in inferential statistics.
What is the rare event rule mentioned in the transcript?
-The rare event rule states that if, under a given assumption, the probability of a particular observed event is extremely small, we conclude that the assumption is most likely incorrect.
What is an event in the context of probability?
-An event is any collection of results or outcomes of a procedure.
What is a simple event?
-A simple event is an outcome or event that cannot be further broken down into simpler components.
What is the sample space in probability?
-The sample space is the collection of all possible outcomes.
How is the sample space for a woman having three children represented in the transcript?
-The sample space for a woman having three children is represented by all possible combinations of male and female births, such as male male male, male male female, and so on.
What are the three approaches to probability mentioned in the transcript?
-The three approaches to probability mentioned are the relative frequency approximation, the classical approach, and the subjective approach.
How is the probability of an event calculated using the relative frequency approximation?
-The probability of an event using the relative frequency approximation is calculated by dividing the number of times the event occurred by the total number of trials.
What is the law of large numbers?
-The law of large numbers states that as a procedure is repeated, the relative frequency of an event tends to approach the actual probability of the event.
What is the addition rule for probability?
-The addition rule for probability states that the probability of either event A or event B occurring is the probability of A plus the probability of B minus the probability of A and B both occurring (to avoid double counting).
How is the probability of a disjoint event calculated?
-For disjoint events, which cannot occur at the same time, the probability is calculated as the sum of the probabilities of each event since there is no overlap to subtract.
What is the probability of selecting a subject who had a positive drug test result or used drugs, according to the example in the transcript?
-The probability of selecting a subject who had a positive drug test result or used drugs is calculated as 0.487, based on the data provided in the transcript.
Outlines
📚 Introduction to Probability and Rare Events
The script begins with an introduction to Chapter 4, focusing on probabilities and their role in inferential statistics. It explains the concept of rare event rules, stating that if the probability of an observed event under a given assumption is very low, the assumption is likely incorrect. The instructor warns students that this section can be challenging and encourages them to seek help. The script then defines key terms such as 'event', 'simple event', and 'sample space', using the example of a woman's childbirth to illustrate these concepts. It further explains the difference between simple and non-simple events, emphasizing the importance of understanding the sample space for accurate probability calculations.
🎯 Understanding Different Approaches to Probability
This paragraph delves into the three main approaches to calculating probability: relative frequency approximation, classical approach, and subjective approach. The relative frequency approach is based on the number of times an event occurs divided by the total number of trials. The classical approach requires equally likely outcomes and calculates the probability as the ratio of favorable outcomes to the total outcomes in the sample space. The subjective approach, on the other hand, estimates probability based on relevant circumstances and expert knowledge. Examples are provided to illustrate each approach, including tossing a coin, rolling a die, and predicting weather conditions.
👶 Sample Space for Gender of Children in a Family
The script presents an example to determine the sample space for the gender of three children in a family. It explains how to calculate the probability of having two boys out of three children using the classical approach, emphasizing the importance of identifying the number of favorable outcomes and the total number of outcomes in the sample space. The example also touches on the concept of sample space size and how it can grow exponentially with the number of events, highlighting the need to understand the size of the sample space for probability calculations.
🏀 Probability in Sports: Reggie Miller's Free Throw Accuracy
This paragraph discusses the application of probability in sports, specifically using the example of NBA player Reggie Miller's free throw success rate. It demonstrates the use of the relative frequency approximation approach by calculating the probability of Miller making a free throw based on his career statistics. The summary emphasizes the high accuracy of Miller's free throws, suggesting that he is a reliable shooter from the free-throw line.
🚗 The Unlikeliness of Meteorite-Car Collisions
The script briefly mentions the probability of a car being struck by a meteorite, suggesting that this would be an example of using the subjective approach to probability due to the lack of concrete data on such rare events. It implies that the probability of such an event is extremely low, highlighting the use of expert knowledge and relevant circumstances in estimating probabilities for events with little historical data.
🔢 The Law of Large Numbers and Probability Boundaries
The Law of Large Numbers (LLN) is introduced, stating that as an event is repeated, the relative frequency of the event tends to approach the actual probability. The script uses the example of flipping a coin to illustrate how the true probability of the event (50/50 heads/tails) will eventually manifest over a large number of trials. It also discusses the boundaries of probability, which must fall between zero and one, inclusive. The concept of complementary events and the complement rule are explained, showing how to calculate the probability of an event not occurring by subtracting the event's probability from one.
📊 Applying the Addition Rule to Probability
The Addition Rule for probability is explained, which is used to find the probability of either event A or event B occurring. The rule states that the probability of A or B is the sum of their individual probabilities minus the probability of both A and B occurring together (to avoid double counting). The script uses a Venn diagram to visually represent the concept and provides a real-world example involving pre-employment drug screening test results. It demonstrates how to calculate the probability of selecting a subject with a positive test result and the probability of selecting a subject who actually used drugs, as well as the combined probability using the Addition Rule.
🤝 Disjoint Events and Their Probabilities
The script discusses the scenario where events A and B are disjoint, meaning they cannot occur simultaneously. In such cases, the Addition Rule simplifies to the sum of the probabilities of A and B since there is no overlap to subtract. An example involving political affiliation is given, where the probability of an American being either a Republican or a Democrat is calculated by simply adding the individual probabilities of each affiliation, assuming they are mutually exclusive.
🏫 Wrapping Up the First Video on Probability
The instructor concludes the first video on probability, summarizing the key points covered and indicating that the chapter will be continued in subsequent videos. The summary includes a brief recap of the topics discussed, such as the different approaches to probability, the Law of Large Numbers, the Addition Rule, and the concept of disjoint events. The instructor thanks the viewers and expresses anticipation for further discussions in class.
Mindmap
Keywords
💡Probabilities
💡Inferential Statistics
💡Sample Space
💡Simple Event
💡Relative Frequency
💡Classical Approach
💡Subjective Approach
💡Law of Large Numbers
💡Complementary Events
💡Addition Rule
Highlights
Introduction to Chapter 4 focusing on probabilities in inferential statistics.
Explanation of the rare event rule and its implication on assumptions in statistics.
Clarification on the difficulty level of the probability section for many students.
Definition of an event and the concept of a simple event in probability.
Illustration of sample space with examples of gender outcomes in single and multiple births.
Differentiation between simple and non-simple events using birth gender examples.
Introduction to probability notation and its equivalence in set theory.
Emphasis on using three significant digits in probability calculations.
Introduction of three approaches to probability: relative frequency, classical, and subjective.
Explanation of the relative frequency approximation in determining probabilities.
Description of the classical approach to probability requiring equally likely outcomes.
Application of the subjective approach using expert knowledge, such as meteorologists predicting rain.
Example of calculating probabilities using the sample space of children's gender.
Discussion on the law of large numbers and its relation to actual probability.
Explanation of the probability range between zero and one and its implications.
Introduction to complementary events and the complement rule in probability.
Example of calculating the probability of being a smoker using two methods.
Introduction to the addition rule in probability for finding the likelihood of one or more events occurring.
Application of the addition rule using a pre-employment drug screening example.
Explanation of disjoint events and their simplification in the addition rule.
Example of calculating the probability of political affiliation as either Republican or Democrat.
Transcripts
Browse More Related Video

Statistics Lecture 4.2: Introduction to Probability

4.1.2 Basics of Probability - Four Approaches to Find or Estimate Probabilities
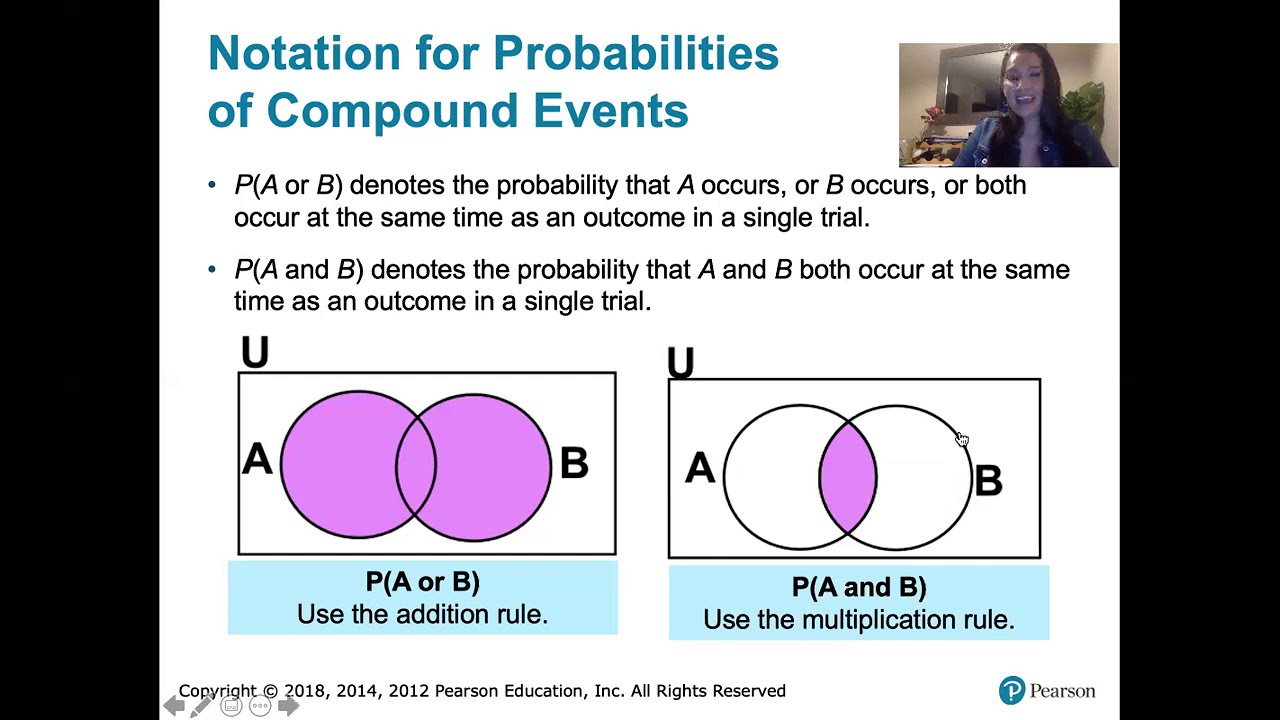
4.2.1 Addition and Multiplication Rules - Simple and Compound Events, and Their Probabilities

Chapter 4 Probability Part 1

4.1.0 Basics of Probability - Lesson Overview, Key Concepts and Learning Outcomes

4.2.3 Addition and Multiplication Rules - Disjoint Events and Implications for Probability
5.0 / 5 (0 votes)
Thanks for rating: