Chapter 4 Probability Part 1

Joan DeRosa
15 Sept 201715:46
EducationalLearning
32 Likes 10 Comments

TLDRThis script delves into the fundamental concepts of probability, defining key terms such as probability experiment, outcomes, sample space, and events. It illustrates these concepts with examples like rolling a die and tossing a coin, employing tree diagrams for visual clarity. The script also explains different types of probabilities, including theoretical and experimental probabilities, and emphasizes the importance of the law of large numbers in approaching theoretical probabilities. It concludes with practical examples of calculating probabilities and the use of complements in probability, adhering to the rounding rules for precision.

Takeaways
  • 🎲 The probability experiment is a process that leads to well-defined results, known as outcomes.
  • 🔄 An outcome is a single result from a trial of a probability experiment.
  • 🌐 The sample space is the set of all possible outcomes of an experiment.
  • 🎯 An event is any collection of outcomes from a probability experiment.
  • 📝 Probabilities are expressed as fractions, decimals, or percentages, ranging from 0 to 1 or 0 to 100.
  • 🎯 Rolling a six-sided die is an example of a probability experiment, with the sample space being 1 through 6.
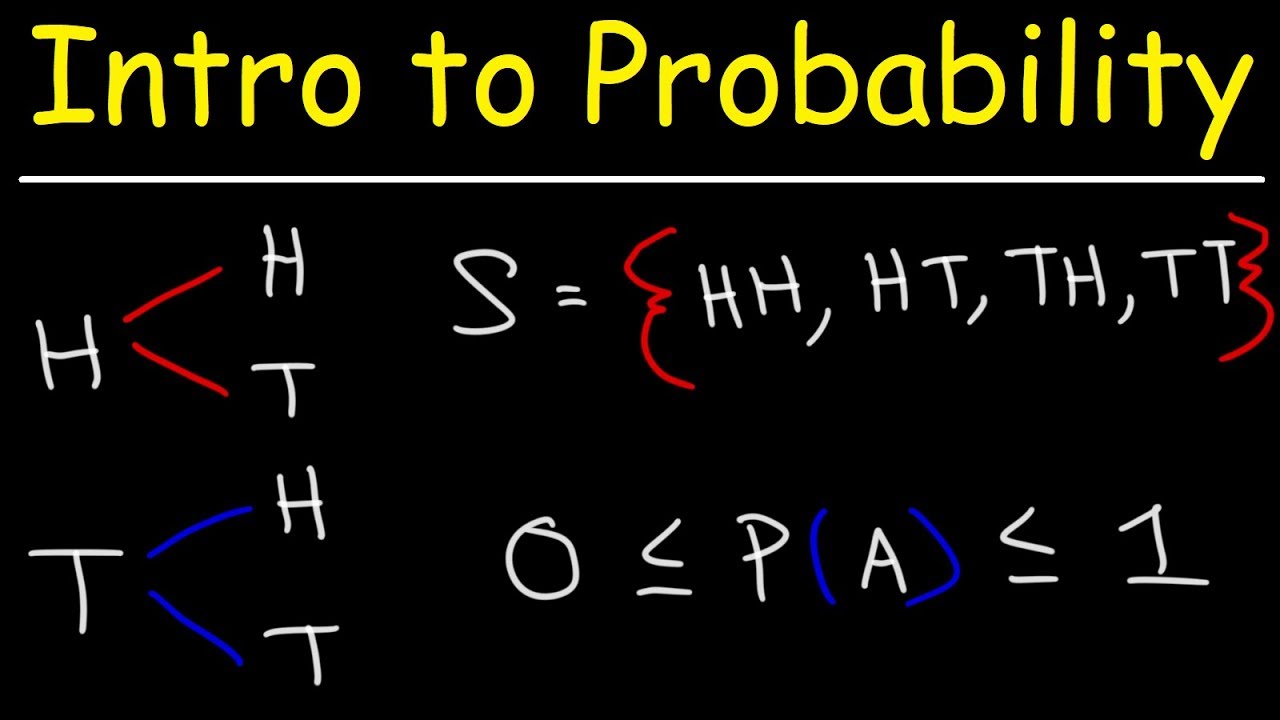
  • 🌳 Tree diagrams are a visual tool to represent the sample space of a probability experiment.
  • 🎰 Tossing a coin and rolling a die is an example where the sample space is the combination of coin outcomes and die results.
  • 🔢 The total number of outcomes is crucial for calculating probabilities.
  • 📐 Simple events consist of a single outcome, unlike composite events that have multiple outcomes.
  • 📊 Probability symbols often include 'P' for probability and capital letters like 'A', 'B', 'C' for events.
  • 📉 The range of probabilities is always between 0 and 1, inclusive, representing impossibility to certainty.
  • 📚 Classical or theoretical probability assumes equally likely outcomes, calculated by dividing favorable outcomes by total outcomes.
  • 🔬 Experimental probability is based on the relative frequency of outcomes in experiments, which approaches theoretical probability as the number of trials increases.
  • 📝 The law of large numbers states that the relative frequency will get closer to the theoretical probability with more trials.
  • 📐 When expressing probabilities, use exact fractions or decimals, or round to three significant digits if not an exact fraction.
  • 📊 Complements of events are the outcomes not included in the event, and the sum of an event and its complement is always 1.
  • 📌 Finding the probability of an event can be done by subtracting the complement's probability from 1.
Q & A

  • What is a probability experiment?

    -A probability experiment is a process that leads to well-defined results, known as outcomes, and is conducted over a set of trials.

  • What is an outcome in the context of probability?

    -An outcome is the result of a single trial of a probability experiment.

  • Can you define the sample space in probability?

    -The sample space is the set of all possible outcomes of a probability experiment.

  • What is an event in probability theory?

    -An event is any collection of results or outcomes from a probability experiment.

  • How are probabilities typically represented?

    -Probabilities are represented as fractions, decimals between 0 and 1, or percentages between 0 and 100.

  • What is a simple event in probability?

    -A simple event is an event that consists of a single outcome.

  • What is a tree diagram in the context of probability?

    -A tree diagram is a visual display used to represent the sample space of a probability experiment, showing all possible outcomes.

  • What is the range of possible values for a probability?

    -The range of possible values for a probability is between 0 and 1, inclusive. It cannot be negative or greater than 1.

  • What is the difference between theoretical probability and experimental probability?

    -Theoretical probability is based on the assumption of equally likely outcomes, while experimental probability is based on the relative frequency of outcomes observed in actual experiments.

  • What is the law of large numbers in relation to probability?

    -The law of large numbers states that as an experiment is repeated, the relative frequency of an event will approach its theoretical probability.

  • How should probabilities be rounded when expressed?

    -Probabilities should be expressed to three significant digits or three decimal places, using the rounding rule for probabilities.

  • Can you explain the concept of a complement of an event?

    -The complement of an event is the set of all outcomes in the sample space that are not included in the event. It is denoted with a line over the event symbol (e.g., A').

  • How do you calculate the probability of an event not happening, given its complement's probability?

    -To find the probability of an event not happening, subtract the probability of the complement from 1 (1 - P(A')).

Outlines
00:00
🎲 Basic Concepts of Probability

This paragraph introduces the fundamental concepts of probability. It defines a probability experiment as a process with well-defined results called outcomes. The sample space is the set of all possible outcomes, and an event is a collection of these outcomes. Probabilities are expressed as fractions, decimals, or percentages ranging from 0 to 1. The paragraph uses the example of rolling a die to explain these concepts, detailing the sample space and how to calculate the probability of an event, such as rolling an even number. It also introduces the concept of a tree diagram as a visual tool for displaying the sample space, using the example of tossing a coin and rolling a die.

05:01
📊 Types of Probability and Calculation Methods

The second paragraph delves into different types of probabilities, such as classical or theoretical probability where outcomes are equally likely, and experimental probability which is based on the relative frequency of outcomes in repeated experiments. The law of large numbers is mentioned, which states that as experiments are repeated, the relative frequency will approach the theoretical probability. The paragraph also covers the rounding rules for expressing probabilities and provides an example of calculating the probability of a high school student texting while driving based on survey data.

10:02
📊 Probability Calculations from Frequency Distributions

This paragraph discusses how to calculate probabilities from frequency distribution tables. It explains the process of finding the total number of observations and identifying the frequency of the favorable outcomes to calculate the probability of an event. An example is given where a company conducts a telephone survey to gauge people's impressions of the 2000s, and the probability of the next person surveyed having a positive impression is calculated. The importance of using the rounding rule for probabilities is emphasized.

15:06
🔄 Complements of Events and Their Probabilities

The final paragraph introduces the concept of complements of events, which are all outcomes in the sample space that are not part of a given event. It explains how the sum of the probabilities of an event and its complement equals one, and how to calculate the probability of an event by subtracting the probability of its complement from one. An example is provided where the probability of choosing an employee not between the ages of 25 and 34 is calculated using the complement rule, and the importance of understanding the complement in probability calculations is highlighted.

Mindmap
Keywords
💡Probability
Probability is a fundamental concept in statistics that quantifies the likelihood of a given event occurring. It is a number between 0 and 1, where 0 indicates impossibility and 1 indicates certainty. In the video, probability is used to explain the likelihood of various outcomes in experiments, such as rolling a die or tossing a coin, and is central to understanding the script's theme of basic probability concepts.
💡Experiment
An experiment in the context of probability is a process that leads to one of several possible outcomes. The video script uses the example of rolling a die as an experiment, where each roll results in an outcome, and the collection of all possible outcomes is known as the sample space.
💡Outcome
An outcome is the result of a single trial of a probability experiment. It represents a single occurrence that can happen during an experiment. In the script, rolling a die and getting a '3' is an example of an outcome, which contributes to the understanding of the sample space for that experiment.
💡Sample Space
The sample space is the set of all possible outcomes of a probability experiment. It is used to visualize and calculate the probabilities of different events. The script illustrates this with the example of rolling a six-sided die, where the sample space is the numbers 1 through 6.
💡Event
An event is a collection of outcomes from a probability experiment. It can be a single outcome or a combination of outcomes. The script defines an event as 'rolling a die and getting an even number,' which includes the outcomes 2, 4, and 6.
💡Tree Diagram
A tree diagram is a visual representation used to display all possible outcomes of a probability experiment. It helps in organizing and understanding complex experiments with multiple steps, such as tossing a coin and then rolling a die, as explained in the script.
💡Simple Event
A simple event is an event that consists of a single outcome. The script clarifies this by contrasting it with events that have more than one outcome, using the example of 'tossing heads and rolling a three' as a simple event.
💡Theoretical Probability
Theoretical probability is calculated by dividing the number of favorable outcomes by the total number of possible outcomes, assuming all outcomes are equally likely. The script mentions this in the context of a fair coin toss, where the probability of getting heads is one out of two.
💡Experimental Probability
Experimental probability, also known as relative frequency, is the approximation of probability based on the observed outcomes of an experiment. The script explains this by discussing how the actual results of tossing a coin multiple times may not always result in a 50-50 split, but the relative frequency will approach the theoretical probability as the number of trials increases.
💡Law of Large Numbers
The law of large numbers is a principle that states that as the number of trials in an experiment increases, the experimental probability will converge to the theoretical probability. The script refers to this law to explain how repeated experiments can help in approximating the true probability of an event.
💡Complement
The complement of an event is the set of all outcomes in the sample space that are not included in the event. The script uses the complement to calculate the probability of not choosing an employee between the ages of 25 and 34 by subtracting the number of employees in that age range from the total and then finding the probability of the remaining outcomes.
Highlights

Probability experiments are processes with well-defined results called outcomes.

An outcome is the result of a single trial of a probability experiment.

The sample space is the set of all possible outcomes of an experiment.

An event is a collection of results or outcomes from a procedure.

Probabilities are expressed as fractions, decimals, or percentages ranging from 0 to 1 or 0 to 100.

Example of a probability experiment: rolling a six-sided die with outcomes 1 through 6.

Tree diagrams provide a visual display of the sample space for probability experiments.

Simple events consist of a single outcome, unlike complex events with multiple outcomes.

The probability of an event is denoted by P(A), B, or C, and calculated using favorable outcomes over total outcomes.

Theoretical probability assumes equally likely outcomes, calculated as favorable outcomes divided by total outcomes.

Experimental probability is based on relative frequency, which approaches theoretical probability as experiments are repeated.

The law of large numbers states that relative frequency will approach theoretical probability with a large number of experiments.

Rounding rules for probabilities suggest expressing them to three significant digits or decimal places.

Complements of an event are all outcomes not included in the event, denoted by A' or an apostrophe.

The sum of the probability of an event and its complement is always 1.

Examples illustrate calculating probabilities using both theoretical and experimental data.

Frequency distribution tables can be used to calculate probabilities of specific outcomes.

Transcripts

Browse More Related Video

Introduction to Probability, Basic Overview - Sample Space, & Tree Diagrams

What is probability | Expected Values, Frequency Distribution, Complement

Math 119 Chapter 4 Part 1

Statistics Lecture 4.2: Introduction to Probability

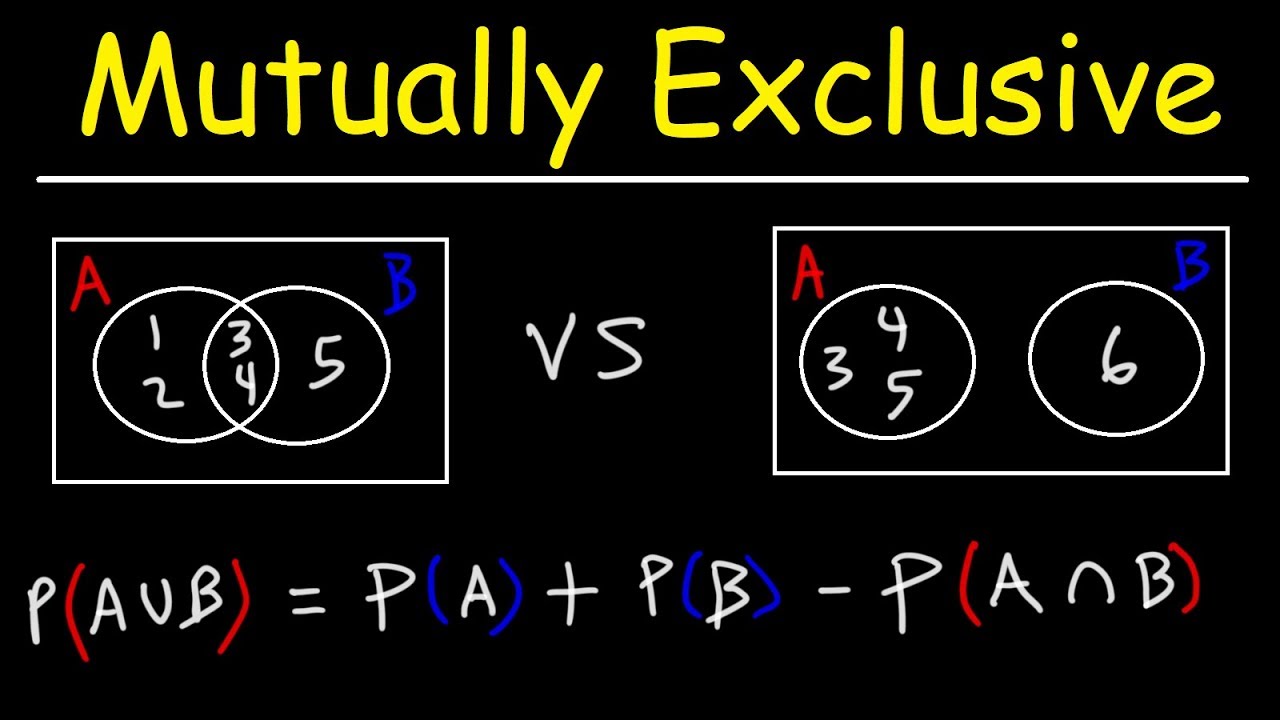
Probability of Mutually Exclusive Events With Venn Diagrams

4.1.0 Basics of Probability - Lesson Overview, Key Concepts and Learning Outcomes

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Probability TheorySample SpaceOutcomesEventsExperimentsTree DiagramComplementsClassical ProbabilityExperimental ProbabilityLaw of Large Numbers