The Pythagorean Theorem

Professor Dave Explains
22 Oct 201705:01
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains the Pythagorean theorem, an important mathematical relationship applying to right triangles. It states that the square of the hypotenuse (the longest side opposite the right angle) equals the sum of the squares of the other two sides, known as the legs. This relationship allows calculation of the third side's length when given the other two. The script gives examples of using the theorem with integers and variables, explaining how substitution and algebra can derive missing side lengths. It promises future discussion on a proof involving area calculation to confirm why the theorem reliably models right triangles.

Takeaways
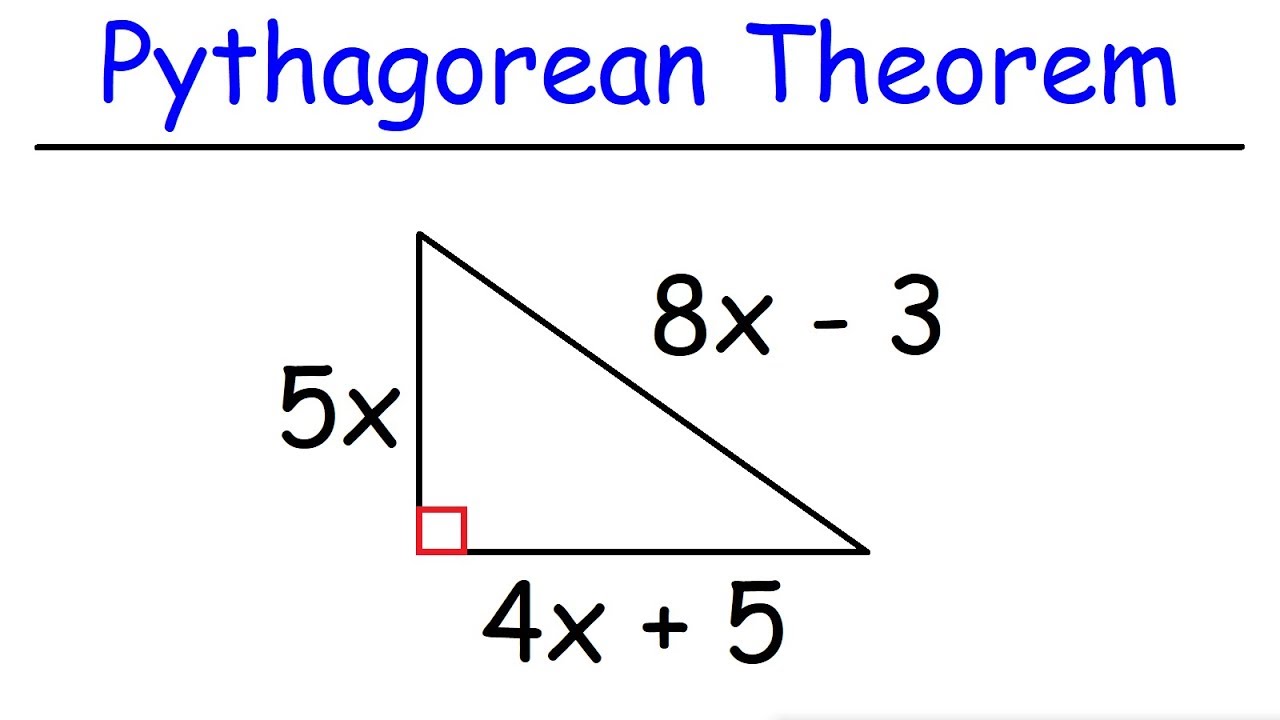
  • 😀 The Pythagorean Theorem relates the sides of a right triangle: a^2 + b^2 = c^2, where a and b are the legs and c is the hypotenuse
  • 📐 In a right triangle, one angle is 90 degrees by definition and the side opposite this right angle is called the hypotenuse
  • 🤓 The theorem is named after Pythagoras, though it was likely discovered earlier
  • 🔢 Using the theorem, if you know 2 side lengths you can calculate the third side length
  • ✏️ We can plug variables for side lengths into the equation and algebraically solve for a missing side
  • 👩‍🔬 The theorem allows you to indirectly measure distances if you only have access to one side and know the angles
  • ❓ The script promises a proof showing why the theorem is true using area calculations
  • 🧮 The lengths of triangle sides may not always be nice integers, so get used to square roots
  • 🔭 The theorem is very useful and common in mathematics
  • 🤔 Understanding how the theorem was derived requires calculating areas of certain shapes
Q & A

  • What is the Pythagorean Theorem?

    -The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides (or legs).

  • Who is the Pythagorean Theorem named after?

    -The Pythagorean Theorem is named after the ancient Greek mathematician Pythagoras, although the theorem was likely discovered prior to Ancient Greece.

  • What are the parts of a right triangle called?

    -The two sides that meet at a 90 degree angle are called the legs, and the side opposite the 90 degree angle is called the hypotenuse.

  • How can you use the Pythagorean Theorem to calculate the third side of a triangle if you know the other two side lengths?

    -Plug the known side lengths into the equation a^2 + b^2 = c^2, where a and b are the known legs and c is the unknown side length. Solve for the unknown variable.

  • How can you apply algebra concepts to the Pythagorean Theorem?

    -You can plug algebraic expressions or variables into the Pythagorean Theorem equation instead of just numbers. This allows you to create equations and solve for unknown lengths.

  • Why do you discard the negative solution when solving for a side length?

    -The lengths of the sides of a triangle cannot be negative. The negative solution does not make physical sense when talking about side lengths, so it is discarded.

  • What makes the Pythagorean Theorem so useful in math?

    -The Pythagorean Theorem allows you to relate the side lengths of right triangles algebraically. This makes it very useful for solving geometry and trigonometry problems across many fields.

  • How can you prove that the Pythagorean Theorem is true?

    -A complete proof requires calculating areas of certain shapes. The professor promises to return to this question soon.

  • What is an example of a right triangle side length problem solved using the Pythagorean Theorem?

    -If one leg is 5 units and the other leg is 12 units, then using the Theorem, the hypotenuse must be 13 units.

  • What are some examples of situations where the Pythagorean Theorem would be applied?

    -The Pythagorean Theorem can be used in geometry, engineering, carpentry, physics, and many other areas requiring calculations with right triangles.

Outlines
00:00
😀 Explaining the Pythagorean Theorem

This paragraph introduces the Pythagorean Theorem, an important mathematical relationship applying to right triangles. It states that the square of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the other two sides. This can be written as a^2 + b^2 = c^2, where c is the hypotenuse. The theorem is named after Pythagoras, though it was likely discovered earlier. Using this relationship, if you know the lengths of any two sides of a right triangle, you can calculate the third side.

Mindmap
Keywords
💡Pythagorean Theorem
The Pythagorean Theorem is a mathematical relationship that relates the lengths of the sides of a right triangle, stating that the square of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the other two sides. This is a central concept in the video, as Professor Dave introduces it and provides examples of how to apply it to calculate missing side lengths.
💡right triangle
A right triangle is a triangle that contains one 90 degree internal angle. The two sides forming this right angle are called the legs, while the third side is called the hypotenuse. Right triangles are essential for applying the Pythagorean Theorem, which only works on right triangles.
💡hypotenuse
The hypotenuse is the longest side of a right triangle, opposite the 90 degree angle. According to the Pythagorean Theorem, the square of the hypotenuse equals the sum of the squares of the other two sides (legs) of a right triangle.
💡legs
The two sides of a right triangle that form the 90 degree angle are called the legs. The Pythagorean Theorem relates the sum of the squares of these leg lengths to the square of the hypotenuse.
💡square
Squaring a number means multiplying it by itself. The Pythagorean Theorem involves squaring the lengths of the triangle sides, such as when calculating 5^2 + 12^2 = 169.
💡algebra
Algebra allows unknown values to be represented by variables like X and solved for logically. Professor Dave demonstrates applying algebraic concepts to the Pythagorean Theorem to solve for an unknown triangle side length.
💡area
The professor notes that satisfactorily proving the Pythagorean Theorem requires calculating areas of certain shapes, foreshadowing an upcoming lesson on this concept and how it relates.
💡proof
A proof is a logical argument demonstrating why a mathematical relationship or theorem must be true in all cases. Professor Dave says a proof of the Pythagorean Theorem will be provided later.
💡squared
Squaring means to multiply a number by itself. This operation is applied to the lengths of the triangle sides in the Pythagorean Theorem equation (A^2 + B^2 = C^2).
💡simplify
To simplify in algebra means to rewrite an expression in an equivalent form but without radicals or other complications, as when Professor Dave simplifies root 56 as root 4 times root 14.
Highlights

Discusses an important theorem relating the side lengths of a right triangle called the Pythagorean theorem

The theorem states that the sum of the squares of the legs equals the square of the hypotenuse

Given 2 sides of a right triangle, we can calculate the third side using the theorem

Provides an example of using known leg lengths to calculate the hypotenuse

We can also use the theorem with 1 known leg and the hypotenuse to find the other leg

Demonstrates plugging variables into the theorem and solving algebraically

Asks how the theorem was derived and promises to revisit this question later

Names the theorem after Pythagoras, though it was likely discovered earlier

Defines key elements of a right triangle - the legs and hypotenuse

Negative length values don't apply, so we discard negative solutions

Irrational hypotenuse lengths are possible when simplified

Useful and commonly applied across mathematics

An impressive logical feat relating geometry and algebra

Likely discovered prior to Ancient Greece

One of the most famous mathematical relationships

Transcripts

Browse More Related Video

Pythagorean Theorem - Basic Introduction

How Do You Know When to Use Cos or Sin in Physics? : Physics & Math

Trigonometry - How To Solve Right Triangles

Trig - 0.6 Trig Functions of Acute Angles

Trigonometry: Finding missing sides and angles

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

Rate This

5.0 / 5 (0 votes)

Thanks for rating: