Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)
TLDRThis video script is an in-depth exploration of trigonometry, specifically focusing on its application to right triangles. The presenter begins by contrasting the traditional approach of using the unit circle with a new perspective that centers on triangles. The video carefully explains how to label the sides of a right triangle as hypotenuse, opposite, and adjacent relative to a given angle, which is essential for applying trigonometric functions. The core trigonometric functions—sine, cosine, and tangent—are defined in the context of a right triangle as ratios of the sides relative to an angle. The script also introduces the reciprocal trigonometric functions—cosecant, secant, and cotangent—and demonstrates how they relate to the primary functions. The presenter uses the Pythagorean theorem to find missing side lengths, which is crucial for calculating the trigonometric functions. The video emphasizes the mnemonic 'sohcahtoa' to remember the relationships between angles and sides. Additionally, the script delves into the concept of complementary angles and how they relate to co-functions, presenting the identity that allows for the interchange between sine and cosine, tangent and cotangent, and secant and cosecant by adjusting for 90 degrees. The video concludes with a promise to cover finding missing sides and angles in future content, ensuring that viewers are left eager for more.
Takeaways
- 📐 **Understanding Trigonometry in Triangles**: The video emphasizes transitioning from viewing trigonometric functions in the context of a unit circle to relating them to the sides of a right triangle.
- 🔄 **Labeling Sides of a Triangle**: It is crucial to label the sides of a right triangle as hypotenuse, opposite, and adjacent with respect to the given angle (theta).
- 📏 **Defining Trig Functions for Right Triangles**: Trigonometric functions for a right triangle are defined as sine (opposite over hypotenuse), cosine (adjacent over hypotenuse), and tangent (opposite over adjacent).
- 🔺 **Reciprocal Trigonometric Functions**: The reciprocal functions are introduced as cosecant (hypotenuse over opposite), secant (hypotenuse over adjacent), and cotangent (adjacent over opposite).
- 🧮 **Applying the Pythagorean Theorem**: The video demonstrates using the Pythagorean theorem to find missing sides in a right triangle, which is essential for calculating trigonometric functions.
- 📈 **Calculating Trig Functions Step by Step**: The process of finding all six trig functions involves identifying the angle, labeling the sides, finding the hypotenuse using the Pythagorean theorem, and then calculating the trig functions.
- 🔁 **Cofunctions and Complementary Angles**: The video explains that cofunctions of complementary angles (angles that add up to 90 degrees) are equal, leading to the identity sine(θ) = cosine(90 - θ).
- 🔀 **Changing Between Trig Functions**: It is shown how to convert one trigonometric function to its cofunction by subtracting the angle from 90 degrees, which is useful for simplifying expressions.
- ✅ **Rationalizing Denominators**: The script mentions the importance of rationalizing the denominator when expressing trigonometric function values to avoid irrational numbers.
- 🔲 **Pythagorean Identity**: The video concludes with the Pythagorean identity, which states that sine squared θ plus cosine squared θ equals one, highlighting the fundamental relationship between these trigonometric functions.
- 🔍 **Practical Application**: The presenter encourages practicing finding missing sides and angles using right triangle trigonometry, emphasizing the practical application of the concepts taught.
Q & A
What is the primary focus of this video on trigonometry?
-The video primarily focuses on the application of trigonometric functions in relation to a right triangle, as opposed to the unit circle.
How does the sine function relate to a right triangle?
-In a right triangle, the sine function relates to the ratio of the length of the side opposite an angle to the length of the hypotenuse (opposite/hypotenuse).
What is the cosine function in the context of a right triangle?
-The cosine function in a right triangle is the ratio of the length of the adjacent side to the length of the hypotenuse (adjacent/hypotenuse).
How is the tangent function defined for a right triangle?
-The tangent function in a right triangle is the ratio of the length of the side opposite an angle to the length of the adjacent side (opposite/adjacent).
What are the reciprocal functions of sine, cosine, and tangent in trigonometry?
-The reciprocal functions of sine, cosine, and tangent are cosecant (cosecant), secant (sec), and cotangent (cot), respectively.
What is the significance of the Pythagorean theorem in the context of right triangle trigonometry?
-The Pythagorean theorem is used to find the length of the hypotenuse or one of the other sides if the lengths of the other two sides are known, which is essential for calculating the trigonometric functions of the angles in the triangle.
What is the relationship between the angles in a right triangle?
-The angles in a right triangle always add up to 180 degrees, with one angle being a right angle (90 degrees), making the other two angles complementary, as they add up to 90 degrees.
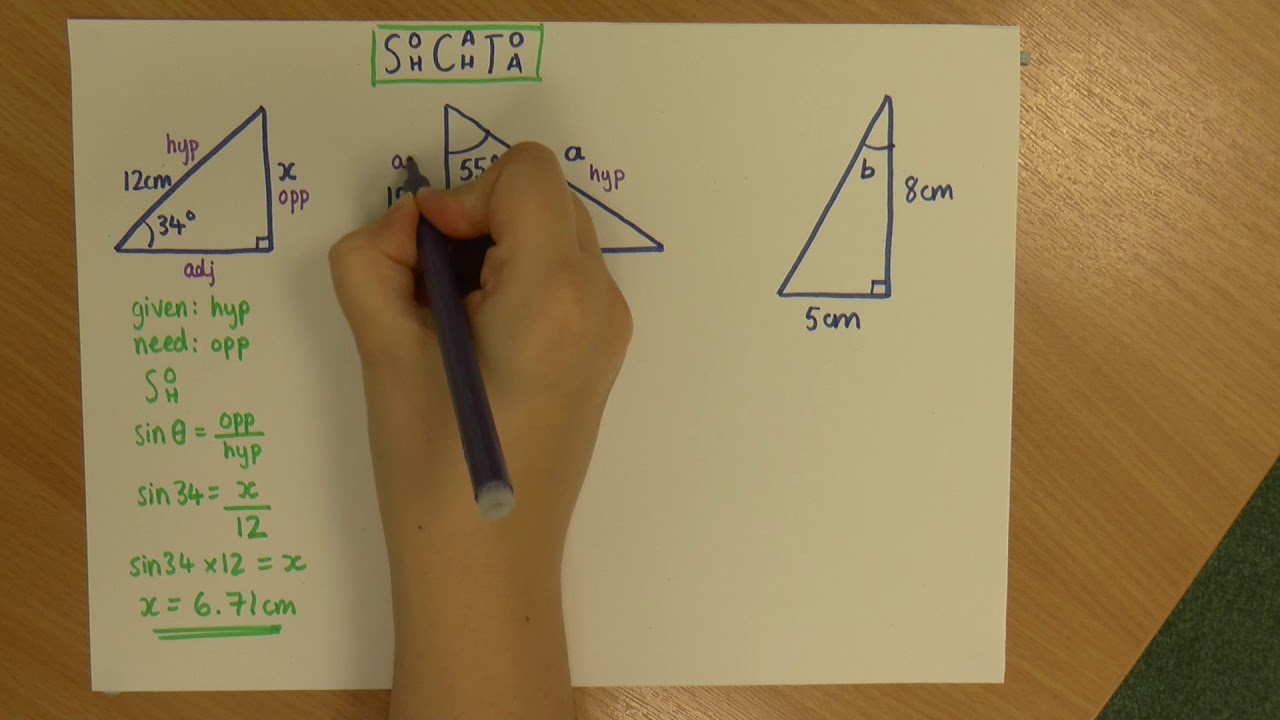
What is the SOHCAHTOA mnemonic used for in trigonometry?
-The SOHCAHTOA mnemonic is used to remember the basic trigonometric ratios for right triangles: Sine is Opposite over Hypotenuse, Cosine is Adjacent over Hypotenuse, and Tangent is Opposite over Adjacent.
How can you find the missing sides of a right triangle using trigonometric functions?
-You can find the missing sides of a right triangle by identifying the hypotenuse, the angle in question, and then using the trigonometric functions (sine, cosine, tangent) to relate the angle to the sides of the triangle and apply the Pythagorean theorem as needed.
Why are sine and cosine referred to as co-functions?
-Sine and cosine are referred to as co-functions because they are complementary to each other, meaning that the sine of one angle in a right triangle is equal to the cosine of its complementary angle.
What is the Pythagorean identity involving sine and cosine?
-The Pythagorean identity involving sine and cosine states that for any angle, the square of the sine of the angle plus the square of the cosine of the angle equals one (sin²θ + cos²θ = 1).
Outlines
📐 Introduction to Trigonometry and the Unit Circle
The video begins by discussing the traditional approach to trigonometry, which involves the unit circle. It explains the basic trigonometric functions—sine, cosine, and tangent—in the context of a circle with a radius, possibly not unit-sized. The focus is on how these functions relate to the coordinates of points on the circle, with sine corresponding to the y-coordinate over the radius (y/r), cosine to the x-coordinate over the radius (x/r), and tangent as the ratio of the y-coordinate to the x-coordinate (y/x). The video emphasizes the shift from only considering the unit circle to a broader understanding of trigonometric functions.
🔶 Transitioning to Triangle Trigonometry
The script transitions from the unit circle to trigonometry in the context of a right triangle. It discusses the labeling of the triangle's sides as opposite, adjacent, and hypotenuse with respect to a chosen angle (theta). The video explains the process of identifying the hypotenuse first and then determining the opposite and adjacent sides based on the angle in question. It also touches on the concept that the hypotenuse remains constant across different angles within the same right triangle.
📐 Defining Trig Functions for Right Triangles
The video script delves into the definitions of sine, cosine, and tangent in the context of a right triangle. It states that sine (sin) corresponds to the ratio of the opposite side to the hypotenuse (opposite/hypotenuse), cosine (cos) to the adjacent side over the hypotenuse (adjacent/hypotenuse), and tangent (tan) as the ratio of the opposite side to the adjacent side (opposite/adjacent). The script also explains the relationship between the Pythagorean theorem and trigonometric functions, indicating how the theorem can be used to find missing sides in a right triangle.
🔁 Reciprocal Trigonometric Functions
The script introduces the reciprocal trigonometric functions—cosecant, secant, and cotangent—and explains their relationships with the primary functions (sin, cos, and tan). It shows how to derive these reciprocal functions using the relationships: cosecant is the reciprocal of sine (hypotenuse/opposite), secant is the reciprocal of cosine (hypotenuse/adjacent), and cotangent is the reciprocal of tangent (adjacent/opposite). The video also recaps the process of applying the unit circle approach to right triangles.
🤝 The Connection Between Trigonometric Functions and Sides of a Triangle
The video emphasizes the connection between trigonometric functions and the sides of a right triangle. It outlines the process of identifying the hypotenuse, locating the given angle, and then finding the opposite and adjacent sides. The script provides a mnemonic, SOHCAHTOA, to remember the relationships: sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, and tangent is opposite over adjacent. It also discusses the application of the Pythagorean theorem in the context of right triangle trigonometry.
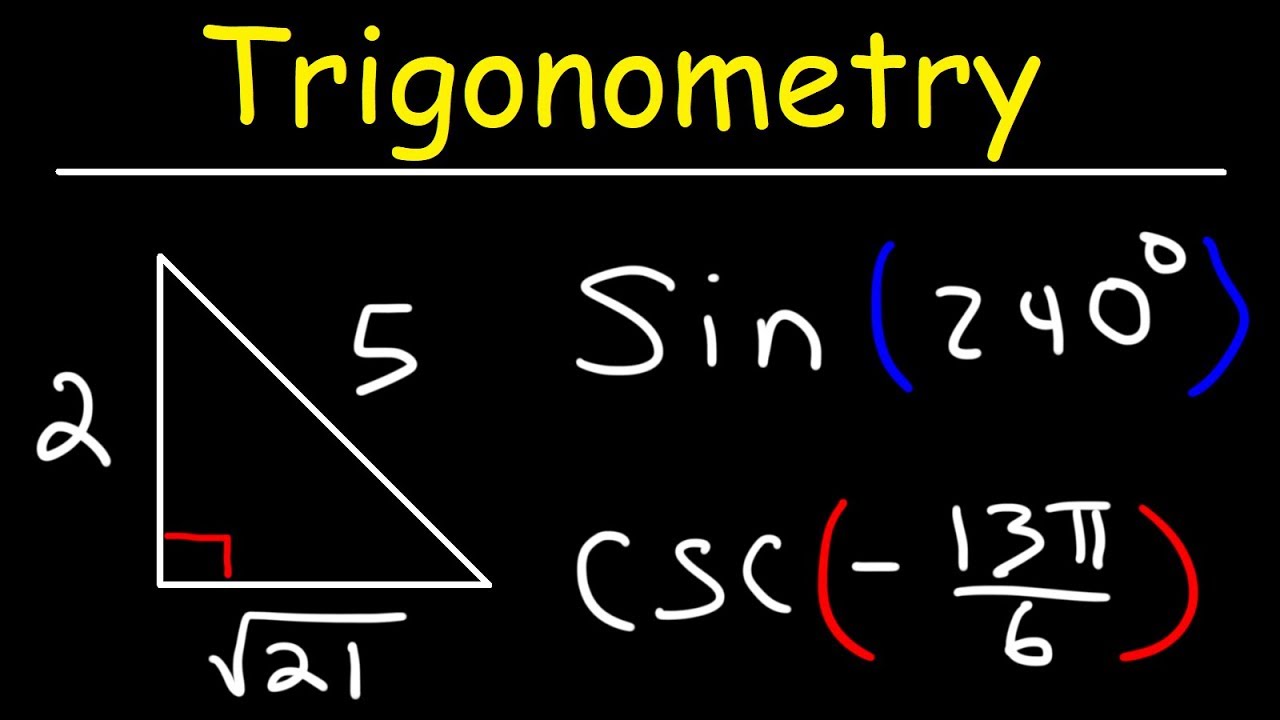
🧮 Applying the Pythagorean Theorem and Finding Trig Functions
The script provides a detailed example of how to apply the Pythagorean theorem to find the hypotenuse of a right triangle when the lengths of the other two sides are known. It then demonstrates how to calculate the primary trigonometric functions (sin, cos, and tan) for a given angle in the triangle. The process involves identifying the angle, labeling the sides as opposite and adjacent, and then calculating the trig functions based on these side lengths. The video also touches on the concept of rationalizing denominators in trigonometric expressions.
🔍 Identifying Sides and Finding Trigonometric Functions
The video script guides viewers through the process of identifying the sides of a right triangle relative to a given angle and then finding the six primary trigonometric functions. It emphasizes the importance of labeling the hypotenuse, identifying the angle, and determining the opposite and adjacent sides before calculating the trig functions. The script also provides methods to find the missing side using the Pythagorean theorem and then uses this information to calculate sine, cosine, tangent, and their reciprocals.
🤔 Understanding Complementary Angles and Co-functions
The video explores the concept of complementary angles in a right triangle, which sum up to 90 degrees. It explains the relationship between the trigonometric functions of complementary angles, stating that the co-functions of complementary angles are equal. This leads to the introduction of trigonometric identities that relate sine and cosine, tangent and cotangent, and secant and cosecant. The script provides examples of how to convert between these functions using the identity involving 90 degrees minus the angle.
🔁 Using Co-function Identities for Trigonometric Simplification
The script illustrates how to use the concept of co-functions to simplify trigonometric expressions. It provides examples of changing one trigonometric function into its co-function by subtracting the angle from 90 degrees, which can simplify calculations and expressions. The video also shows how to apply this concept to combine trigonometric terms and utilize known identities, such as the Pythagorean identity, to further simplify expressions.
📚 Summary of Right Triangle Trigonometry
The video concludes with a summary of the concepts covered, emphasizing the understanding of right triangle trigonometry and the ability to relate an angle to two sides of a triangle using sine, cosine, and tangent. It also highlights the importance of knowing how to label sides as opposite and adjacent to a given angle and how to use the Pythagorean theorem to find missing sides. The video promises a follow-up on finding missing sides and angles using right triangle trigonometry.
Mindmap
Keywords
💡Trigonometry
💡Unit Circle
💡Right Triangle
💡Hypotenuse
💡Opposite Side
💡Adjacent Side
💡Sine Function
💡Cosine Function
💡Tangent Function
💡Reciprocal Functions
💡Pythagorean Theorem
Highlights
The video focuses on the transition from understanding trigonometric functions in the context of a unit circle to applying them to right triangles.
Explains the concept that sine, cosine, and tangent are related to the y-coordinate, x-coordinate, and the ratio of y to x in a unit circle, respectively.
Introduces the labeling of sides in a right triangle as hypotenuse, opposite, and adjacent in relation to a given angle.
Demonstrates that sine in a right triangle is the ratio of the opposite side to the hypotenuse.
Clarifies that cosine is the ratio of the adjacent side to the hypotenuse in a right triangle.
Tangent is shown to be the ratio of the opposite side to the adjacent side in a right triangle.
Discusses the reciprocal relationships of the primary trigonometric functions to their reciprocal functions (cosecant, secant, and cotangent).
Uses the Pythagorean theorem to find missing sides in a right triangle, which is crucial for calculating all six trigonometric functions.
Provides a mnemonic, SOHCAHTOA, to remember the relationships between sine, cosine, and tangent with the sides of a right triangle.
Illustrates how to rationalize the denominator when dealing with trigonometric expressions.
Shows how to apply the Pythagorean theorem to find the hypotenuse when given two other sides of a right triangle.
Demonstrates the process of finding all six trigonometric functions for a given angle in a right triangle.
Introduces the concept of complementary angles in a right triangle and how they relate to the co-functions of trigonometric ratios.
Explains that the co-functions of complementary angles are equal, providing a powerful tool for simplifying trigonometric expressions.
Provides identities for converting between sine and cosine, tangent and cotangent, secant and cosecant by using the concept of complementary angles.
Demonstrates how to simplify expressions using the Pythagorean identity, which states that sine squared plus cosine squared equals one.
The video concludes with a promise to cover how to find missing sides and angles with right triangle trigonometry in a future video.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: