Pythagorean Theorem - Basic Introduction
TLDRThis educational video script introduces the Pythagorean theorem, a fundamental principle for understanding the relationship between the sides of a right triangle. It begins with a basic explanation and progresses to solving example problems, illustrating how to calculate the hypotenuse when given the lengths of the other two sides. The script then tackles a more complex problem involving algebraic expressions for the sides of a triangle, guiding viewers through the process of using the Pythagorean theorem to find the integer value of the longest side. The explanation is clear and methodical, providing a comprehensive understanding of how to apply the theorem to solve for missing side lengths in right triangles.
Takeaways
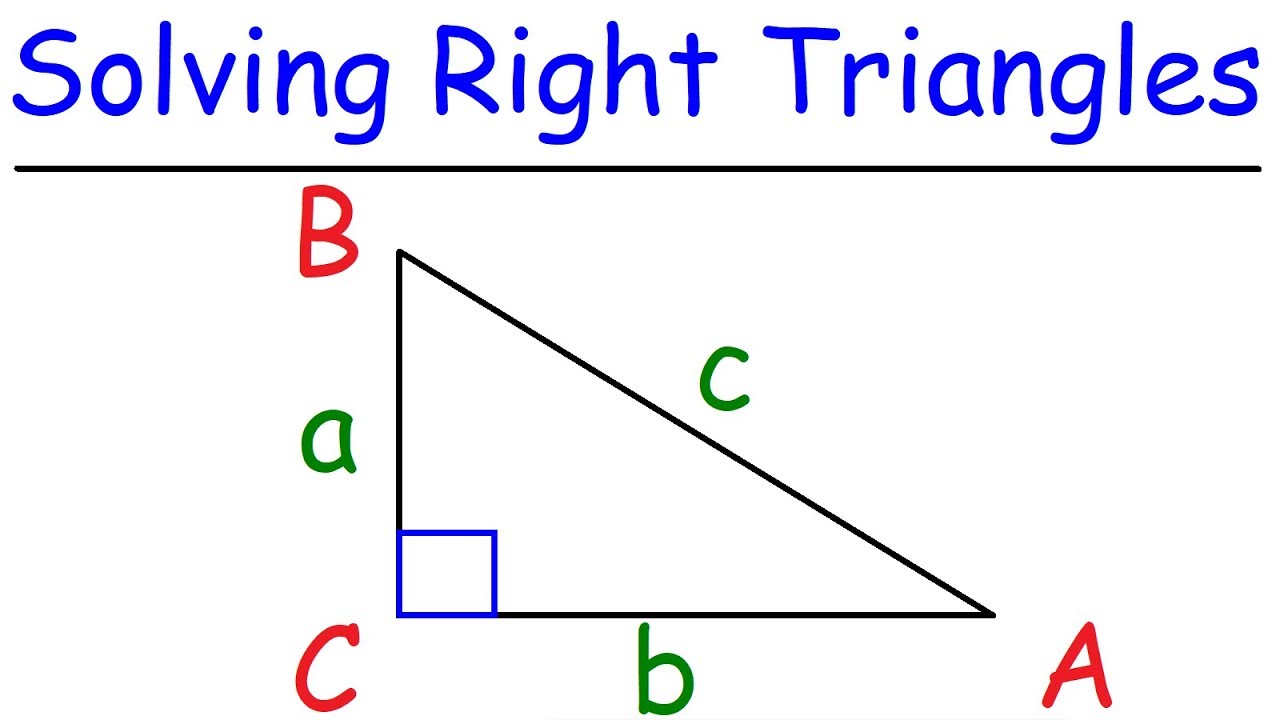
- 📚 The Pythagorean theorem is fundamental for understanding the relationship between the sides of a right triangle, where \( a^2 + b^2 = c^2 \).
- 🔍 The hypotenuse (c) is the longest side of a right triangle and is opposite the right angle.
- 📐 The video provides a step-by-step example of how to use the Pythagorean theorem to find the length of the hypotenuse when the lengths of the other two sides are known.
- 🧩 The process involves squaring the lengths of the two known sides, adding them together, and then taking the square root of the sum to find the hypotenuse.
- 📈 The script includes a more complex example where the lengths of the sides are represented by algebraic expressions, requiring the use of the Pythagorean theorem to solve for the unknown variable.
- 📝 The video demonstrates how to expand and simplify algebraic expressions when applying the Pythagorean theorem to a triangle with sides in the form of polynomials.
- 🔢 The quadratic formula is introduced as a method to solve for the variable when the Pythagorean theorem results in a quadratic equation.
- ❗ The importance of considering only the positive solution when determining the length of a side is emphasized, as side lengths are positive values.
- 📉 The video concludes by solving the initial problem, finding the integer value of the hypotenuse to be 29 for the given right triangle with sides represented by expressions.
- 👍 The script serves as a comprehensive tutorial on applying the Pythagorean theorem to find missing sides of right triangles, including those with algebraic expressions.
- 👨🏫 The presenter encourages viewers to subscribe and turn on notifications for more educational content, highlighting the interactive and instructive nature of the video.
Q & A
What is the Pythagorean theorem and how does it relate to right triangles?
-The Pythagorean theorem is a fundamental principle in geometry that states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. It is represented as a^2 + b^2 = c^2, where c is the hypotenuse, and a and b are the other two sides.
What are the three sides of a right triangle called?
-In a right triangle, the three sides are referred to as follows: the side adjacent to the right angle (often labeled as 'a'), the side opposite the right angle (often labeled as 'b'), and the hypotenuse, which is the longest side and is opposite the right angle (often labeled as 'c').
How does the video script introduce the Pythagorean theorem?
-The video script introduces the Pythagorean theorem by explaining its basic concept and formula, and then it proceeds to demonstrate its application through example problems involving right triangles.
What is the purpose of the video script's example problems?
-The purpose of the example problems in the video script is to illustrate how to apply the Pythagorean theorem to find the missing side of a right triangle, thus helping viewers understand and practice the concept.
In the video script, what is the formula used to calculate the missing side of a right triangle?
-The formula used to calculate the missing side of a right triangle, as per the video script, is a^2 + b^2 = c^2, where c is the hypotenuse and a and b are the other two sides of the triangle.
How does the video script handle the case where the hypotenuse is given as X and the legs are 5 and 12?
-The video script solves for X by setting up the equation 5^2 + 12^2 = X^2, calculating 5^2 as 25 and 12^2 as 144, adding them to get 169, and then taking the square root of 169 to find that X = 13.
What is the main problem presented in the video script, and how is it approached?
-The main problem presented in the video script is to find the integer value of the longest side of a right triangle when the sides are given as 5, 4X + 5, and 8X - 3. The problem is approached by setting up the Pythagorean theorem equation and solving for X using algebraic methods.
What algebraic method is suggested in the video script to solve for X in the main problem?
-The video script suggests using the quadratic formula to solve for X in the main problem, as the resulting equation from the Pythagorean theorem is a quadratic equation that is difficult to factor.
How does the video script ensure that the solution for X is a positive integer?
-The video script ensures that the solution for X is a positive integer by discarding the negative solution obtained from the quadratic formula, as side lengths cannot be negative.
What is the final answer for the longest side of the triangle in the main problem presented in the video script?
-The final answer for the longest side of the triangle, which is the hypotenuse, is 29, as determined by substituting the positive integer value of X back into the equation for the hypotenuse 8X - 3.
What is the significance of the video script's explanation of the Pythagorean theorem in educational terms?
-The video script's explanation of the Pythagorean theorem is significant in educational terms as it provides a clear and step-by-step guide for learners to understand and apply a fundamental concept in geometry, thus enhancing their mathematical skills and knowledge.
Outlines
📚 Introduction to the Pythagorean Theorem
This paragraph introduces the Pythagorean theorem, a fundamental principle in geometry that defines the relationship between the sides of a right triangle. It explains the theorem's formula, a^2 + b^2 = c^2, where c represents the hypotenuse, the longest side of the triangle. The speaker provides a brief tutorial on how to use the theorem to find the missing side of a right triangle, using an example with sides 5 and 12 to find the hypotenuse X. The process involves squaring the known side lengths, adding them together, and then taking the square root of the result to find X. The explanation emphasizes the use of positive values for the length of a side and concludes with the solution that X = 13.
🔍 Solving More Complex Right Triangle Problems
The second paragraph delves into solving more complex problems involving right triangles. The speaker presents a scenario where the hypotenuse is 10 units long, and one leg is 5 units, challenging the viewer to find the length of the missing side. The process involves applying the Pythagorean theorem, a^2 + b^2 = c^2, with a = X, b = 5, and c = 10. The calculation leads to the equation 5^2 + X^2 = 10^2, which simplifies to X^2 = 75. The solution for X is the square root of 75, which is approximately 8.66 when expressed as a decimal. This example illustrates how to handle non-perfect squares and emphasizes the importance of using positive values for side lengths.
🎯 Applying the Pythagorean Theorem to a Challenging Problem
The final paragraph presents a challenging problem involving a right triangle with sides expressed as algebraic expressions: 5X, 4X + 5, and 8X - 3. The goal is to determine the integer value of the longest side, which is the hypotenuse. The speaker guides the viewer through the application of the Pythagorean theorem to these expressions, resulting in a quadratic equation. The equation is simplified and solved using the quadratic formula, yielding two potential solutions for X. However, since a side length cannot be negative, the negative solution is discarded, and X = 4 is accepted. Substituting X back into the expressions for the sides, the speaker calculates the lengths as 20, 21, and 29, identifying 29 as the integer value of the hypotenuse. The paragraph concludes with a summary of the process and a reminder of the Pythagorean theorem's utility in solving for missing sides of right triangles.
Mindmap
Keywords
💡Pythagorean theorem
💡Hypotenuse
💡Right triangle
💡Legs of a triangle
💡Square root
💡Quadratic equation
💡Binomial
💡Foil method
💡Quadratic formula
💡Integer value
💡Like terms
Highlights
Introduction to the Pythagorean theorem and its application in right triangles.
Explanation of the relationship between the sides of a right triangle using the Pythagorean theorem.
Description of the hypotenuse as the longest side of a right triangle.
Formula for calculating the missing side of a right triangle: \( a^2 + b^2 = c^2 \).
Example problem solving with a hypotenuse X and legs 5 and 12.
Mathematical process of squaring and adding the squares of the legs to find the hypotenuse.
Use of positive value for the length of a side in geometric problems.
Another example with a hypotenuse of 10 units, one leg of 5, and finding the missing side.
Demonstration of isolating and solving for X using subtraction and square roots.
Introduction of the problem with sides 5, \( 4X + 5 \), and \( 8X - 3 \).
Setting up the Pythagorean theorem equation for the given triangle sides.
Expansion and combination of terms for the binomial expressions.
Rearrangement of the equation to solve for the hypotenuse C.
Application of the quadratic formula to solve for X.
Calculation of the discriminant and the square root to find the value of X.
Rejection of negative X value due to the physical impossibility of negative side lengths.
Substitution of X value back into the triangle sides to find the lengths.
Conclusion with the integer value of the longest side, the hypotenuse, being 29.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: