Trigonometry: Finding missing sides and angles
TLDRIn this engaging video, Rachel guides viewers through the process of solving for missing lengths and angles in right-angled triangles using trigonometry. She begins by emphasizing the importance of identifying the hypotenuse, opposite, and adjacent sides in relation to the given angle. Rachel then demonstrates the application of the SOHCAHTOA mnemonic, which corresponds to the trigonometric functions sine, cosine, and tangent. Through three distinct examples, she shows how to use these functions to find missing side lengths and angles. In the first example, she uses the sine function to find the length of the opposite side when given the hypotenuse and an angle. The second example illustrates the use of the cosine function to determine the hypotenuse when the adjacent side and an angle are provided. Finally, Rachel tackles an angle problem, where she employs the tangent function to find an unknown angle given the lengths of the opposite and adjacent sides. She also highlights the utility of calculators for performing these calculations and encourages viewers to review her previous video for further clarification on identifying triangle sides. This video serves as an accessible and informative resource for those looking to enhance their understanding of trigonometry in the context of right-angled triangles.
Takeaways
- 🔺 The tutorial focuses on finding missing lengths and angles in right-angled triangles using trigonometry, covering three example problems.
- 📐 'SOHCAHTOA' is introduced as the essential mnemonic to remember the trigonometric ratios: Sine, Cosine, and Tangent.
- 📏 The first example calculates a missing side (opposite) in a triangle using the sine function with given angle and hypotenuse values.
- ✏️ Rachel emphasizes the method of rearranging the equation, sine 34 = x/12, to isolate and solve for x, which represents the length of the side.
- 🔍 The second example involves finding the hypotenuse using the cosine function, given the adjacent side and an angle.
- 🔄 Detailed explanation of the rearrangement process is provided: swapping the denominator with the cosine value on the left-hand side of the equation to solve for the hypotenuse.
- 📋 The third example shifts to finding a missing angle using the tangent function and given side lengths (opposite and adjacent).
- ⚙️ Rachel illustrates how to calculate the angle by using the inverse of the tangent function (arctan or tan^-1) to find the degree of the angle from the tangent ratio.
- 🔢 The tutorial includes step-by-step calculations using a calculator for all trigonometric functions involved.
- 🎓 There's a recommendation to watch previous videos for viewers needing a refresher on identifying triangle sides (hypotenuse, opposite, adjacent) and equation rearrangement techniques.
Q & A
What is the primary educational goal of the video discussed in the transcript?
-The primary educational goal of the video is to teach viewers how to find missing lengths and angles in right-angled triangles using trigonometry.
What trigonometric acronym is introduced in the video?
-The acronym introduced in the video for remembering trigonometric ratios is SOHCAHTOA.
How does the presenter intend to help viewers unfamiliar with identifying sides of a triangle?
-The presenter suggests that viewers who are not comfortable with identifying the sides of a triangle (hypotenuse, opposite, adjacent) watch her previous video on that specific topic for better understanding.
In the example involving the first triangle, which trigonometric function is used and why?
-In the first triangle example, the sine function is used because the sides involved are the hypotenuse and the opposite side, and according to SOHCAHTOA, sine relates these two sides.
What method does the presenter use to solve for the unknown side labeled 'X' in the first triangle example?
-The presenter solves for 'X' by rearranging the sine equation, multiplying both sides by the length of the hypotenuse to isolate 'X' on one side, which involves basic algebraic manipulation.
What are the steps taken to find the length of the hypotenuse in the second triangle example?
-To find the length of the hypotenuse in the second triangle, the presenter uses the cosine function, sets up the equation with the given adjacent side and unknown hypotenuse, and then rearranges it to solve for the hypotenuse by dividing the length of the adjacent side by the cosine of the angle.
How is the missing angle found in the third triangle example?
-The missing angle in the third triangle is found by using the tangent function, which involves the opposite and adjacent sides. The presenter calculates the tangent of the angle, and then uses the inverse tangent function to find the angle itself.
What calculator function does the presenter highlight as useful when doing trigonometric calculations?
-The presenter highlights the 'answer' button on the calculator, which can be used to utilize the result of the previous calculation directly in the next calculation, streamlining the process.
Why is it important not to use the right angle when applying trigonometric functions in these examples?
-It's important not to use the right angle because trigonometric functions in right-angled triangle problems are based on the angles that are not right angles (acute angles). Using the right angle would not provide the correct relationships between the sides of the triangle.
What practical tips does the presenter offer for rearranging equations to solve for unknowns in trigonometry problems?
-The presenter advises thinking of rearranging equations as swapping what is on the left side of the equals sign with what is on the bottom of the fraction on the right side. This approach simplifies the algebra involved in isolating the variable.
Outlines
📐 Trigonometry Basics for Right-Angled Triangles
Rachel introduces the concept of finding missing lengths and angles in right-angled triangles using trigonometry. She begins by explaining the SOHCAHTOA acronym, which aids in identifying the hypotenuse, opposite, and adjacent sides of a triangle. In her example, Rachel focuses on a triangle where she has been given the hypotenuse and needs to find the opposite side. Using the sine function derived from SOHCAHTOA, she demonstrates how to calculate the length of the side opposite the given angle. Rachel's approach simplifies trigonometric calculations and encourages referring to previous tutorials on identifying triangle sides and rearranging equations for those unfamiliar with the processes.
🔍 Applying Trigonometry to Find Sides and Angles
Rachel continues with another example, this time using the cosine function to find the length of a hypotenuse in a triangle, given the adjacent side and an angle. She illustrates the rearrangement of the trigonometric formula to solve for the hypotenuse and uses a calculator for precision. Additionally, Rachel shifts to finding a missing angle using the tangent function, where she is provided with the opposite and adjacent sides. By inserting values into the tangent formula and performing calculations, she determines the unknown angle, showcasing the practical application of inverse trigonometric functions to derive angles from side lengths.
🌟 Summary of Trigonometric Applications
In a brief summary, Rachel encapsulates the usefulness of trigonometry in solving problems related to right-angled triangles, both in finding missing sides and angles. This concise wrap-up underscores the practicality and versatility of trigonometric functions in mathematical problem-solving and geometry.
Mindmap
Keywords
💡Trigonometry
💡Right-angled triangle
💡Hypotenuse
Highlights
Introduction to finding missing lengths and angles in right-angled triangles using trigonometry.
Explanation of the trigonometry acronym SOHCAHTOA and its variants for solving triangle problems.
Identification of triangle sides: hypotenuse, opposite, and adjacent in context.
How to use the sine function to find a missing side when the hypotenuse and an angle are known.
Step-by-step calculation of the side 'X' using sine function and an angle of 34 degrees.
Explanation of rearranging equations to isolate the variable of interest.
Use of a calculator to multiply sine value by the hypotenuse to find the missing length.
Identification of triangle sides for a new problem involving cosine to find the hypotenuse.
Using the cosine function to calculate the hypotenuse when the adjacent side and an angle are known.
Calculation process for the hypotenuse using division and cosine function.
Introduction to solving for a missing angle using the tangent function and known side lengths.
Explanation of using tangent ratio to relate opposite and adjacent sides to find an angle.
Step-by-step guidance on calculating the tangent value using a calculator.
Demonstration of finding an angle using the inverse tangent function.
Concluding remarks on the practical application of trigonometry in solving problems with right-angled triangles.
Transcripts
Browse More Related Video

Trig - 0.6 Trig Functions of Acute Angles

Trigonometry made easy

When Do I use Sin, Cos or Tan?

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)
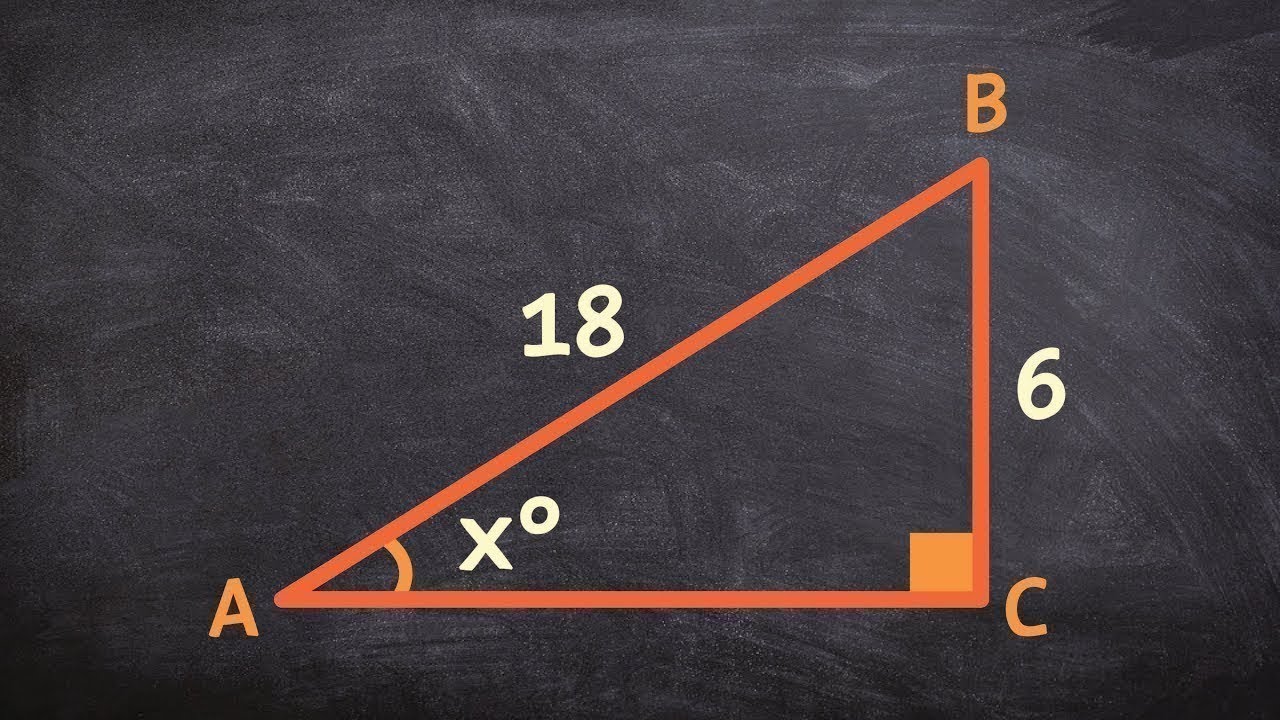
Learn to find the missing angles for a triangle using inverse trig functions

Finding Sides and Angles with Right Triangle Trigonometry (Precalculus - Trigonometry 31)
5.0 / 5 (0 votes)
Thanks for rating: