How Do You Know When to Use Cos or Sin in Physics? : Physics & Math

eHowEducation
1 Oct 201304:19
EducationalLearning
32 Likes 10 Comments

TLDRIn the video script, Cristen Oviedo explains the application of sine and cosine in physics, particularly in relation to right triangles and vector representation. The key concept is that while the Pythagorean theorem helps with right triangles when all sides are known, trigonometry is used when an angle is given. Sine corresponds to the side opposite the angle (theta), and cosine to the adjacent side. This understanding is crucial for working with vectors in physics, as it allows the decomposition of diagonal vectors into their horizontal and vertical components within an XY coordinate system.

Takeaways
  • 📐 The Pythagorean theorem helps find the third side of a right triangle when two sides are known.
  • 📐 Trigonometry is used when only angles and one side (the hypotenuse) are known to find the other sides of a triangle.
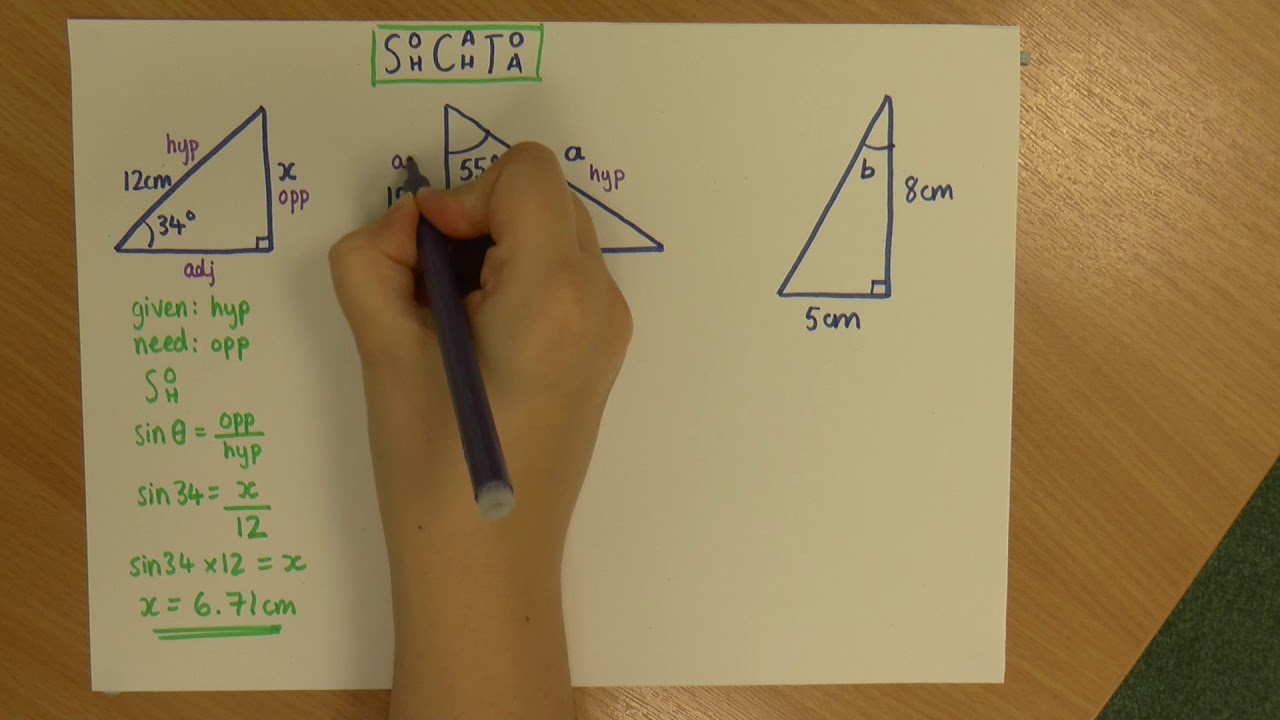
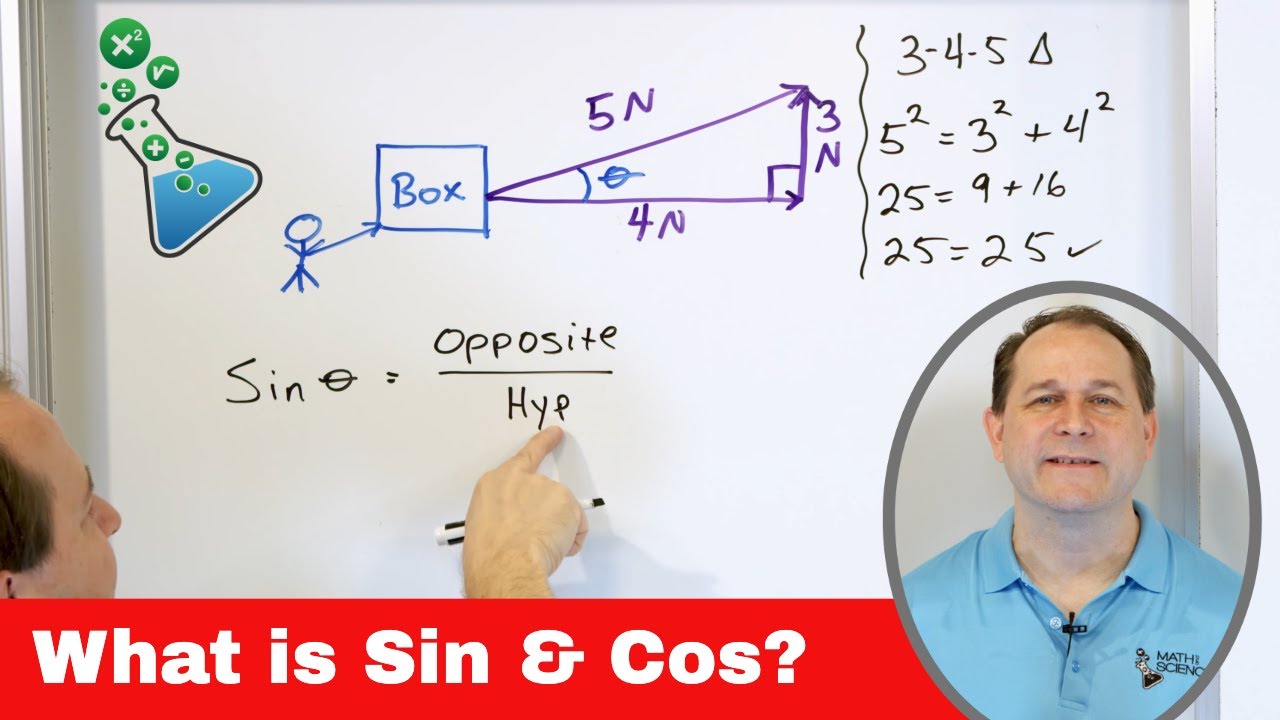
  • 📐 In trigonometry, the sine of an angle (θ) represents the ratio of the opposite side to the hypotenuse (H * sin(θ))
  • 📐 The cosine of an angle (θ) represents the ratio of the adjacent side to the hypotenuse (H * cos(θ))
  • 📐 The hypotenuse is often assumed to be 1 for simplicity, but it can be any number.
  • 📐 Trigonometry is applied to non-right triangles by dividing them into two right triangles.
  • 📐 In physics, trigonometry is used to analyze vectors, which are quantities represented as arrows in space.
  • 📐 Vectors in an XY coordinate system require the use of sine and cosine to determine their horizontal and vertical components.
  • 📐 Sine corresponds to the side opposite the angle, and cosine corresponds to the side adjacent to the angle.
  • 📐 The mnemonic 'sohcahtoa' can be used to remember that sine is opposite, and cosine is adjacent in trigonometry.
  • 👩‍🏫 The speaker, Cristen Oviedo, provides this explanation to clarify when to use sine or cosine in physics.
Q & A

  • What is the Pythagorean theorem and how does it relate to trigonometry?

    -The Pythagorean theorem is a principle in geometry that states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. It is fundamental to trigonometry because it helps in finding the third side of a right triangle when the other two sides are known.

  • Why do we use trigonometry in physics?

    -Trigonometry is used in physics to deal with angles and to find missing sides or angles in a triangle, especially when dealing with vectors which are represented by arrows in space. It allows us to break down vectors into their components along different axes, which is essential for analyzing motion and forces in physics.

  • What is the relationship between sine and cosine functions in the context of a right triangle?

    -In the context of a right triangle, the sine of an angle (θ) is the ratio of the length of the side opposite the angle to the length of the hypotenuse (H), and the cosine of the angle is the ratio of the length of the side adjacent to the angle to the hypotenuse. These ratios are used to find the lengths of the sides of the triangle when one side and the angle are known.

  • How does the hypotenuse affect the sine and cosine values in a right triangle?

    -The hypotenuse (H) is the scaling factor for the sine and cosine values in a right triangle. If the hypotenuse is not equal to one, both the sine and cosine values are multiplied by H to get the actual lengths of the sides opposite and adjacent to the angle θ.

  • What is the significance of the angle θ in trigonometry?

    -The angle θ is significant in trigonometry as it determines the orientation of the triangle and the direction of the sine and cosine values. It is the angle measured in a counterclockwise direction from the positive x-axis (or the base of the triangle) to the line containing the hypotenuse.

  • How can you convert a non-right triangle into right triangles?

    -You can convert a non-right triangle into two right triangles by drawing a perpendicular line from one vertex to the opposite side, creating two right triangles at the point where the line intersects the side. This process is known as 'dropping a perpendicular' and it allows the application of trigonometric principles to find missing sides or angles.

  • What are vectors and how do they relate to trigonometry?

    -Vectors are mathematical objects that represent both a magnitude (length) and a direction. In physics, they are often used to describe quantities like force, velocity, and displacement. Trigonometry is used to break down vectors into their components along the x and y axes, which helps in analyzing the vector's effect in different directions.

  • What does the term 'unit circle' refer to in trigonometry?

    -The unit circle is a circle with a radius of 1, centered at the origin (0,0) of the coordinate plane. It is used in trigonometry to define the sine and cosine functions for all angles, where the x-coordinate of a point on the unit circle corresponds to the cosine of the angle, and the y-coordinate corresponds to the sine of the angle.

  • How do you determine the side opposite to an angle in a right triangle?

    -The side opposite to an angle (θ) in a right triangle is found using the sine function. If you know the hypotenuse (H) and the angle θ, the length of the opposite side is given by the formula: length = H * sin(θ).

  • How do you determine the side adjacent to an angle in a right triangle?

    -The side adjacent to an angle (θ) in a right triangle is found using the cosine function. If you know the hypotenuse (H) and the angle θ, the length of the adjacent side is given by the formula: length = H * cos(θ).

  • What is the mnemonic 'sohcahtoa' mentioned in the script, and how does it relate to sine and cosine?

    -The mnemonic 'sohcahtoa' is a way to remember the order of the trigonometric functions for solving triangles. It stands for Sine (sin), Opposite, Hypotenuse, Cosine (cos), Adjacent, and Tangent (tan). It helps to recall that sine is opposite over hypotenuse, and cosine is adjacent over hypotenuse, which are the basic ratios used in right triangles.

Outlines
00:00
📐 Introduction to Trigonometry and the Pythagorean Theorem

The video begins with Cristen Oviedo explaining the relevance of the Pythagorean theorem in middle school, which helps determine the third side of a right triangle when the other two sides are known. However, in situations where the sides are not given, trigonometry and angles become essential. The video transitions to discussing how trigonometry, using sine and cosine, can be applied when only an angle (denoted by the Greek letter theta) and the hypotenuse (denoted as H) are known. It emphasizes that these trigonometric functions can find the other sides of the triangle when the hypotenuse is scaled appropriately.

Mindmap
Keywords
💡Pythagorean theorem
The Pythagorean theorem is a fundamental principle in geometry that states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This theorem is used to find the missing side of a right triangle when the other two sides are known. In the context of the video, it is mentioned as a basis for understanding trigonometry when not all sides are known.
💡Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. It is used to calculate the angles and sides of a triangle when some of the information is missing. In the video, trigonometry is introduced as a tool to use angles instead of sides to find unknown sides of a triangle, which is particularly useful in physics.
💡Sine
The sine of an angle in a right triangle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. It is one of the primary functions in trigonometry and is used to relate angles to the sides of a triangle. In the video, sine is used to represent the vertical or opposite side when the angle is measured from the bottom side of a right triangle.
💡Cosine
The cosine of an angle in a right triangle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. Like sine, cosine is a fundamental function in trigonometry that helps in determining the relationship between the angles and sides of a triangle. In the video, cosine is used to represent the horizontal or adjacent side when the angle is measured from the bottom side of a right triangle.
💡Hypotenuse
The hypotenuse is the longest side of a right-angled triangle, which is opposite the right angle. It is the side that is used as the reference for calculating the sine and cosine of an angle in the triangle. In the video, the hypotenuse is represented by 'H' and is used to scale the sine and cosine values to find the actual lengths of the other sides.
💡Greek letter theta
In the context of the video, the Greek letter theta (θ) is used to represent an angle in a right triangle. It is a common notation in mathematics and physics to denote angles. The video explains how to use theta in conjunction with the hypotenuse to find the other sides of the triangle using sine and cosine.
💡Vector
A vector is a mathematical object that has both magnitude (length) and direction. In physics, vectors are often represented as arrows in space, indicating both how far and in what direction a quantity extends. The video mentions vectors to explain why trigonometry is important in physics, as it helps in determining the components of vectors in an XY coordinate system.
💡XY coordinate system
The XY coordinate system is a two-dimensional Cartesian coordinate system used to specify the position of a point in a plane. It consists of two perpendicular axes, one horizontal (the X-axis) and one vertical (the Y-axis), intersecting at the origin. In the video, the XY coordinate system is mentioned as a context where trigonometry is used to determine the horizontal (cosine) and vertical (sine) components of vectors.
💡SOHCAHTOA
SOHCAHTOA is a mnemonic used in trigonometry to remember the definitions of the sine, cosine, and tangent functions in relation to the angles and sides of a right triangle. It stands for Sine is Opposite/Hyperbola, Cosine is Adjacent/Hyperbola, and Tangent is Opposite/Adjacent. In the video, the concept is related to the idea of sine being opposite and cosine being adjacent to the angle theta.
💡Physics
Physics is the natural science that studies matter, its motion, and behavior through space and time, and the related entities of energy and force. In the video, physics is mentioned as a field where trigonometry is extensively used, particularly in dealing with vectors and their components.
💡Right triangle
A right triangle is a triangle in which one of the angles is a right angle, meaning it is exactly 90 degrees. The Pythagorean theorem and trigonometric functions are often applied in the context of right triangles to find missing sides or angles. The video discusses the use of trigonometry in right triangles to find the sides when an angle and one side (the hypotenuse) are known.
Highlights

Introduction to the Pythagorean theorem and its application in finding the third side of a right triangle.

The limitation of the Pythagorean theorem when not all sides are known, leading to the use of trigonometry and angles.

Use of trigonometry with given angle (theta) and hypotenuse (H) to find the other sides of a triangle.

Explanation that sine and cosine are used to relate angles to the sides of a triangle when the hypotenuse is scaled to one.

Clarification that sine and cosine values are multiplied by the hypotenuse (H) for proper scaling.

Conversion of any triangle into two right triangles for easier analysis.

Application of trigonometry in physics due to the representation of quantities by vectors.

Vectors in physics often represented as arrows in space, requiring knowledge of their coordinates and extensions in different directions.

Example of using sine and cosine in the context of an XY coordinate system for vector analysis.

General case presentation with theta and H, illustrating the use of H sine theta and H cosine theta.

Explanation of the order of sine and cosine in relation to the angle, not strictly vertical and horizontal.

The concept of sine as the side opposite to theta, and cosine as the side adjacent to theta.

Mnemonic 'sohcahtoa' mentioned as a way to remember trigonometric relationships, with a focus on 'opposite' and 'adjacent' for sine and cosine.

Cristen Oviedo's summary on determining the use of sine or cosine in physics based on the relationship with angle theta.

Transcripts

Browse More Related Video

Trig - 0.6 Trig Functions of Acute Angles

Trigonometry: Finding missing sides and angles

05 - Sine and Cosine - Definition & Meaning - Part 1 - What is Sin(x) & Cos(x) ?

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

17 - Calculating Vector Components in Physics, Part 1 (Component form of a Vector)

How to Use the Law of Sines in Trigonometry (Precalculus - Trigonometry 32)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryPhysicsVectorsSineFunctionCosineFunctionPythagoreanTrigonometryTipsCristenOviedoEducationalContentMathematics