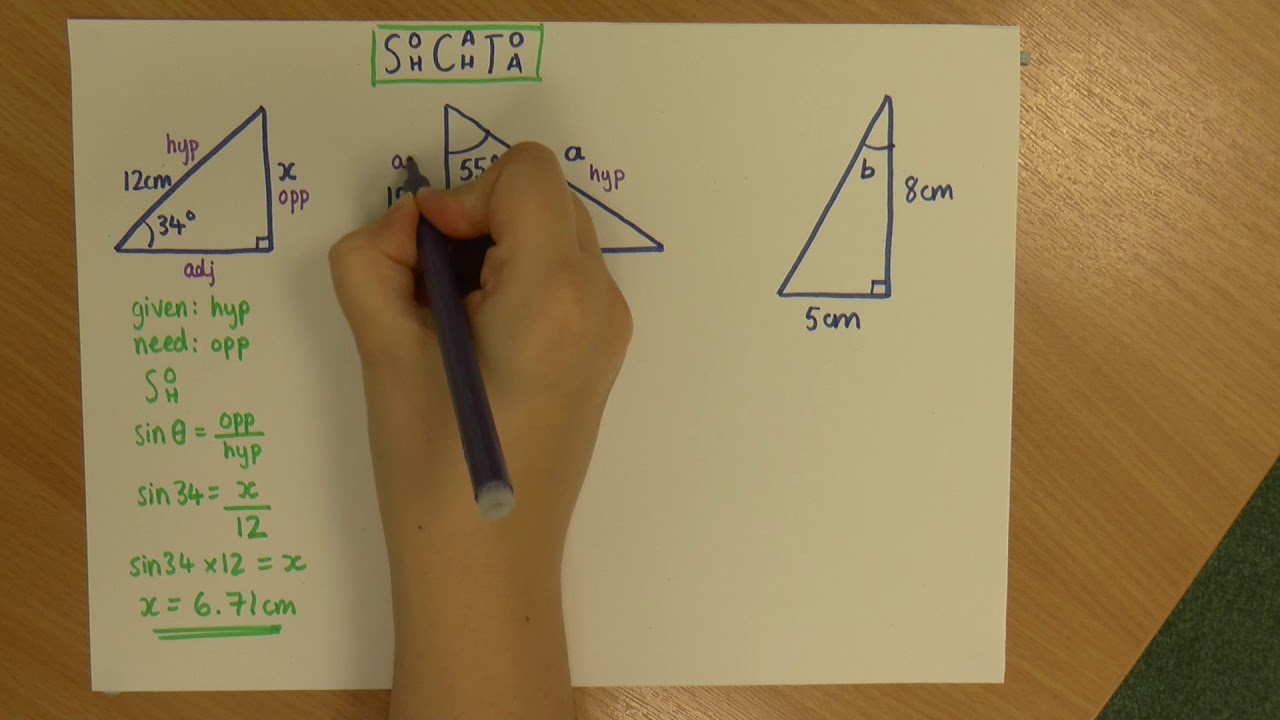
Trig - 0.6 Trig Functions of Acute Angles

Kimberly Brehm
26 Jun 202107:25
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers an insightful exploration into the world of trigonometric functions, specifically focusing on acute angles within right triangles. It begins by defining the key components of a right triangle: the opposite, adjacent, and hypotenuse sides in relation to an angle named theta. The script then introduces the acronym SOHCAHTOA as a mnemonic for understanding the sine, cosine, and tangent ratios. It explains that sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, and tangent is opposite over adjacent. The reciprocal relationships between these trigonometric functions and their co-functions (cosecant, secant, and cotangent) are also highlighted. The video continues with practical examples, illustrating how to calculate the values of these functions given certain side lengths of a triangle. It also demonstrates the process of finding the hypotenuse when not directly provided, using the Pythagorean theorem. The script concludes with a teaser for the next topic: trigonometric functions of any angle, not just acute ones in right triangles, promising an expansion of the concepts introduced.

Takeaways
  • 📐 **Trigonometric Functions in Right Triangles**: The video discusses trigonometric functions for acute angles in right triangles, focusing on the relationships between the sides of the triangle.
  • 🔢 **Defining Acute Angles**: A right triangle has one right angle (90 degrees) and two acute angles that sum to 90 degrees, with one of them being designated as theta.
  • 📐 **Side Definitions**: The sides of a right triangle are defined as opposite (to the angle theta), adjacent (next to the angle theta), and the hypotenuse (the longest side opposite the right angle).
  • 📈 **Trigonometric Ratios**: The video explains the basic trigonometric ratios: sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent).
  • 🧩 **Memory Aid**: Introduces 'sohcahtoa' as a mnemonic to remember the ratios for sine, cosine, and tangent.
  • 🔁 **Reciprocal Ratios**: Corollary functions like cosecant, secant, and cotangent are the reciprocals of sine, cosine, and tangent, respectively.
  • ⚖️ **Example Calculation**: Provides an example of calculating trigonometric functions for a right triangle with given side lengths, using the definitions of sine, cosine, and tangent.
  • 🔢 **Pythagorean Theorem**: Explains the use of the Pythagorean theorem to find the hypotenuse when two sides of a right triangle are known.
  • 📐 **Finding Trigonometric Functions**: Demonstrates how to find sine, cosine, and tangent for a given angle theta using the sides of a right triangle.
  • 🔍 **Rationalizing Denominators**: Highlights the process of rationalizing the denominator to avoid radicals in the final trigonometric function values.
  • 📐 **Applying Trigonometry**: Shows how to apply trigonometric functions to find the values of sine, cosine, and secant given the lengths of the sides of a right triangle.
  • ➡️ **Next Steps**: The video concludes with a teaser for the next topic, which will cover trigonometric functions for any angle, not just acute angles in right triangles.
Q & A

  • What are the three main trigonometric functions related to acute angles in a right triangle?

    -The three main trigonometric functions are sine (sin), cosine (cos), and tangent (tan). Sine is defined as the ratio of the opposite side to the hypotenuse, cosine as the ratio of the adjacent side to the hypotenuse, and tangent as the ratio of the opposite side to the adjacent side.

  • What is the mnemonic 'sohcahtoa' used for?

    -The mnemonic 'sohcahtoa' is used to help remember the definitions of the trigonometric functions sine and cosine, where 'so' stands for 'sine is opposite over hypotenuse' and 'cahtoa' stands for 'cosine adjacent over hypotenuse'.

  • How are the reciprocal trigonometric functions cosecant, secant, and cotangent related to sine, cosine, and tangent respectively?

    -Cosecant (csc) is the reciprocal of sine (sin), secant (sec) is the reciprocal of cosine (cos), and cotangent (cot) is the reciprocal of tangent (tan). This means that if sin(θ) = opposite/hypotenuse, then csc(θ) = hypotenuse/opposite, and similarly for the other functions.

  • In a right triangle, what is the longest side called?

    -In a right triangle, the longest side is called the hypotenuse. It is the side opposite the right angle.

  • If theta is an acute angle in a right triangle, and the opposite side is 24 units, while the hypotenuse is 25 units, what is the value of sine of theta?

    -The value of sine of theta (sin(θ)) is the ratio of the opposite side to the hypotenuse. So, sin(θ) = 24/25.

  • How can you find the hypotenuse of a right triangle if you know the lengths of the other two sides?

    -You can find the hypotenuse (c) of a right triangle using the Pythagorean theorem, which states that the sum of the squares of the other two sides (a and b) is equal to the square of the hypotenuse (c^2 = a^2 + b^2).

  • What is the tangent of theta in a right triangle where the lengths of the legs are 6 cm and 3 cm?

    -The tangent of theta (tan(θ)) is the ratio of the opposite side to the adjacent side. Since theta is the larger acute angle opposite the longer leg, tan(θ) = opposite/adjacent = 6/3 = 2.

  • How do you find the sine of theta if the opposite side is 6 units and the adjacent side is 3 units in a right triangle?

    -To find the sine of theta (sin(θ)), you first need to determine the length of the hypotenuse using the Pythagorean theorem (c^2 = a^2 + b^2). Then, sin(θ) = opposite/hypotenuse. In this case, sin(θ) = 6/√(3^2 + 6^2) = 6/√(9 + 36) = 6/√45.

  • If the tangent of theta is given as 5/12, how would you find the secant of theta?

    -The secant of theta (sec(θ)) is the reciprocal of the cosine of theta (cos(θ)). First, find the hypotenuse using the tangent ratio (tan(θ) = opposite/adjacent), then use the Pythagorean theorem to find the hypotenuse. After that, sec(θ) = hypotenuse/adjacent.

  • What is the process to rationalize the denominator when the denominator contains a radical?

    -To rationalize the denominator, you multiply both the numerator and the denominator by the conjugate of the denominator. If the denominator is √a, the conjugate is √a, and the result will be a fraction with an integer denominator after simplification.

  • How can you remember which trigonometric function to use when given a right triangle and an angle?

    -Use the mnemonic 'sohcahtoa' to remember that sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, and tangent is opposite over adjacent. This can help you determine which sides of the triangle to use for each trigonometric function.

Outlines
00:00
📐 Understanding Trigonometric Functions in Right Triangles

This paragraph introduces the concept of trigonometric functions for acute angles in right triangles. It explains the importance of identifying one of the acute angles, referred to as theta, and how the sides of the triangle relate to this angle. The sides are categorized as opposite, adjacent, and hypotenuse with respect to theta. The trigonometric functions sine, cosine, and tangent are defined in relation to these sides. A mnemonic, 'sohcahtoa', is provided to help remember the relationships: sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, and tangent is opposite over adjacent. The paragraph also touches on the reciprocal relationships between sine and cosecant, as well as cosine and secant. It concludes with an example problem where the sine and tangent of theta are calculated given the lengths of the triangle's sides.

05:00
🔢 Applying Pythagorean Theorem and Finding Trigonometric Ratios

The second paragraph delves into applying the Pythagorean theorem to find an unknown side of a right triangle when only the lengths of the legs are given. It demonstrates how to calculate the hypotenuse when the lengths of the other two sides are known, using the formula 'a squared plus b squared equals c squared'. The paragraph then illustrates how to find the sine of an angle when the hypotenuse is known, by using the ratio of the opposite side to the hypotenuse. It also explains the process of rationalizing the denominator to avoid radicals in the denominator of the fraction. The concept of secant as the inverse of cosine is introduced, and an example is provided to show how to calculate the secant of an angle given the tangent and the lengths of the sides. The paragraph concludes with a teaser for the next topic: trigonometric functions of any angle.

Mindmap
Keywords
💡Trig Functions
Trigonometric functions, often abbreviated as 'trig functions,' are mathematical functions that relate the angles of a triangle to the lengths of its sides. In the context of the video, trig functions are used to describe the relationships between the acute angles and the sides of a right triangle. The video focuses on the trig functions of acute angles, which are sine, cosine, and tangent, and their reciprocals, cosecant, secant, and cotangent.
💡Acute Angles
An acute angle is an angle that is less than 90 degrees. In the video, acute angles are central to understanding trig functions within right triangles. The script discusses how the trig functions are defined based on the sides of a right triangle relative to an acute angle, which the video refers to as 'theta'.
💡Right Triangle
A right triangle is a type of triangle that has one angle that is a right angle, exactly 90 degrees. The video uses right triangles to explore trig functions. It explains that in a right triangle, the two acute angles sum up to 90 degrees, and the longest side opposite the right angle is called the hypotenuse.
💡Sine (sin)
Sine is a trigonometric function defined as the ratio of the length of the side opposite the angle (in a right triangle) to the length of the hypotenuse. In the video, sine is introduced as 'opposite over hypotenuse' and is used to find the sine of theta, which is an example of applying the sine function to a specific angle in a right triangle.
💡Cosine (cos)
Cosine is another trigonometric function that represents the ratio of the adjacent side to the hypotenuse in a right triangle. The video defines cosine as 'adjacent over hypotenuse' and uses it to calculate the cosine of theta, showing how it relates to the sides of the triangle.
💡Tangent (tan)
Tangent is a trig function that is the ratio of the opposite side to the adjacent side in a right triangle. The video explains that tangent is 'opposite over adjacent' and uses this function to find the tangent of theta without needing to calculate the hypotenuse, as it is not part of the tangent's formula.
💡Cosecant (csc)
Cosecant is the reciprocal of the sine function and is defined as the ratio of the hypotenuse to the length of the side opposite the angle. In the video, cosecant is mentioned as the inverse of sine, and the script provides an example of how to calculate the cosecant of theta using the hypotenuse and opposite side.
💡Secant (sec)
Secant is the reciprocal of the cosine function, with the ratio being the hypotenuse to the length of the adjacent side. The video explains secant as 'hypotenuse over adjacent' and shows how to find the secant of theta by first determining the hypotenuse of the triangle.
💡Cotangent (cot)
Cotangent is the reciprocal of the tangent function and is the ratio of the adjacent side to the opposite side in a right triangle. The video defines cotangent as 'adjacent over opposite' and uses it to illustrate the relationship between the sides of the triangle and the angle theta.
💡Hypotenuse
The hypotenuse is the longest side of a right triangle, which is opposite the right angle. The video emphasizes the hypotenuse's role in defining trig functions such as sine, cosine, and tangent. It is used in the formulas for these functions and is often calculated using the Pythagorean theorem when not directly given.
💡Pythagorean Theorem
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. The video uses this theorem to find the hypotenuse when it is not directly provided, which is essential for calculating trig functions that involve the hypotenuse.
💡SOHCAHTOA
SOHCAHTOA is a mnemonic used to remember the definitions of the trig functions sine, cosine, and tangent. The video introduces this mnemonic as a handy way to remember which trig function corresponds to which sides of the triangle. It is particularly useful for students learning trigonometry for the first time.
Highlights

Trig functions are discussed in the context of acute angles in right triangles

In a right triangle, one angle is 90 degrees and the other two are acute, adding up to 90 degrees

The side opposite the acute angle is called the opposite side

The side adjacent to the acute angle is called the adjacent side

The longest side opposite the 90 degree angle is the hypotenuse

Trig functions are defined as sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent)

The acronym SOHCAHTOA helps remember the definitions of sine, cosine, and tangent

Cosecant is the reciprocal of sine, and secant is the reciprocal of cosine

Cotangent is the reciprocal of tangent

Example problem: Given an angle theta and side lengths, find the trig function values

If theta is given, the side lengths define the fractions for the trig function calculations

Pythagorean theorem can be used to find the hypotenuse when it is not given

Example: In a right triangle with legs of 6 and 3 cm, the larger acute angle theta is opposite the longer leg

Tangent of theta can be found directly from the side lengths as opposite/adjacent

Sine of theta requires finding the hypotenuse first using the Pythagorean theorem

Secant of theta is the reciprocal of cosine, calculated as hypotenuse/adjacent

Hypotenuse can be found using the Pythagorean theorem for secant calculation

Next video will cover trig functions of any angle, not just acute angles in right triangles

Transcripts

Browse More Related Video

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

Basic Trigonometry: Sin Cos Tan (NancyPi)

Trigonometry made easy

Trigonometry: Finding missing sides and angles

When Do I use Sin, Cos or Tan?

Which are the Three Functions in Trigonometry? | Don't Memorise

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryAcute AnglesRight TrianglesSine FunctionCosine FunctionTangent FunctionMnemonicsMath EducationGeometryTrig FunctionsInverse RelationsTrig Identities