Power

statslectures
7 Aug 201006:23
EducationalLearning
32 Likes 10 Comments

TLDRThis educational script delves into the concept of statistical power, using the example of a medication designed to enhance typing speed. It explains the null hypothesis, set at an average typing speed of 30 words per minute, and the alternative hypothesis, which assumes the medication increases this average to 46 words per minute. The script outlines the process of calculating standard error and using it to plot distributions under both hypotheses. It then demonstrates how to determine the power of a test, which is the probability of correctly rejecting the null hypothesis when it is false, and beta, the probability of a type II error. By calculating z-scores and referring to a Z-table, the script concludes with an example showing a high power (98%) of correctly rejecting the null hypothesis, and a low type II error rate (2%).

Takeaways
  • 😌 The concept of 'power' in statistics is challenging for some to grasp, and it's being explained through an example involving a new medication that claims to improve typing ability.
  • πŸ” The average typing speed is 30 words per minute (WPM) with a standard deviation of 16. The medication is expected to increase this average to 46 WPM.
  • πŸ“Š A sample of 16 individuals is used to test the medication's effectiveness, and the goal is to determine the probability of correctly concluding its effectiveness through a statistical test.
  • 🎯 The null hypothesis (H0) is that the mean typing speed is 30 WPM, while the alternative hypothesis (H1) is that it's different from 30 WPM.
  • 🧐 Power is defined as the probability of correctly rejecting the null hypothesis when the alternative hypothesis is true, and beta (Ξ²) is the probability of incorrectly retaining the null hypothesis.
  • πŸ“ The standard error is calculated as the standard deviation divided by the square root of the sample size, which in this case is 4.
  • πŸ“‰ The distribution under the null hypothesis is centered at 30 with a standard error of 4, and an alpha level of 0.05 is used to determine critical values.
  • πŸ“ˆ The distribution under the alternative hypothesis is centered at 46 with the same standard error of 4, representing the expected mean if the medication works.
  • πŸ“š The power of the test is represented by the area under the alternative hypothesis distribution that falls outside the critical values determined by the alpha level.
  • πŸ”’ The critical value at 1.96 standard errors from the mean under the null hypothesis corresponds to a z-score calculation under the alternative hypothesis.
  • πŸ“˜ Using a z-table, the area to the body (right tail) corresponding to a z-score of 2.04 (negative of 1.96 in the alternative distribution) is found to be 0.9793, which represents the power of the test.
  • 🚫 The type II error rate, or beta, is calculated as 1 - power, which in this case is 1 - 0.9793 = 0.0207, or 2%.
Q & A

  • What is the concept of 'power' in the context of statistical hypothesis testing?

    -In statistical hypothesis testing, 'power' refers to the probability of correctly rejecting the null hypothesis when the alternative hypothesis is true. It is a measure of the test's ability to detect an effect if there is one.

  • What is the null hypothesis in the context of the medication test for typing ability?

    -The null hypothesis in this scenario is that the average typing speed is 30 words per minute, which is the baseline average before the medication is administered.

  • What is the alternative hypothesis in the medication test for typing ability?

    -The alternative hypothesis is that the medication has an effect and the average typing speed is different from 30 words per minute, with the assumption that it increases to 46 words per minute.

  • What is the significance level (alpha) used in the medication test, and what does it represent?

    -The significance level (alpha) used in the medication test is 0.05. It represents the probability of rejecting the null hypothesis when it is actually true, also known as the Type I error rate.

  • How is the standard error calculated in this scenario?

    -The standard error is calculated by dividing the standard deviation of the population by the square root of the sample size. In this case, the standard deviation is 16, and the sample size is 16, resulting in a standard error of 4.

  • What is the role of the standard error in the hypothesis testing process?

    -The standard error provides a measure of how much the sample mean is expected to vary from sample to sample. It is used to construct confidence intervals and to determine how far an observed mean must be from the hypothesized mean to be statistically significant.

  • What does the term 'Type II error' or 'beta' represent in hypothesis testing?

    -A 'Type II error' or 'beta' is the probability of incorrectly retaining the null hypothesis when it is actually false. It represents the test's failure to detect an effect when there is one.

  • How is the power of a test related to the Type II error?

    -The power of a test is equal to 1 minus the probability of a Type II error (beta). A higher power means a lower probability of making a Type II error, indicating a more sensitive test.

  • What is the difference between the distributions drawn when the null hypothesis is true and when it is false?

    -The distribution when the null hypothesis is true has a mean of 30 words per minute, while the distribution when the null hypothesis is false (assuming the alternative is true) has a mean of 46 words per minute. Both distributions have a standard error of 4.

  • How is the z-score used in calculating the power and Type II error in this scenario?

    -The z-score is calculated by taking the difference between the critical value (37.84 in this case) and the mean under the alternative hypothesis (46), divided by the standard error (4). This z-score is then used to look up the area in the tail of the distribution, which represents the power, and the remaining area represents the Type II error.

  • What is the calculated power of the test in the medication study, and what does it signify?

    -The calculated power of the test is approximately 98%. This means there is a 98% chance that the test will correctly reject the null hypothesis if the medication indeed increases the average typing speed to 46 words per minute.

  • What is the Type II error rate in the medication study, and what does it imply?

    -The Type II error rate, or beta, is 2%. This implies there is a 2% chance that the test will incorrectly fail to reject the null hypothesis when it is actually false, meaning the test might miss the effect of the medication.

Outlines
00:00
πŸ”¬ Understanding Statistical Power in Medication Testing

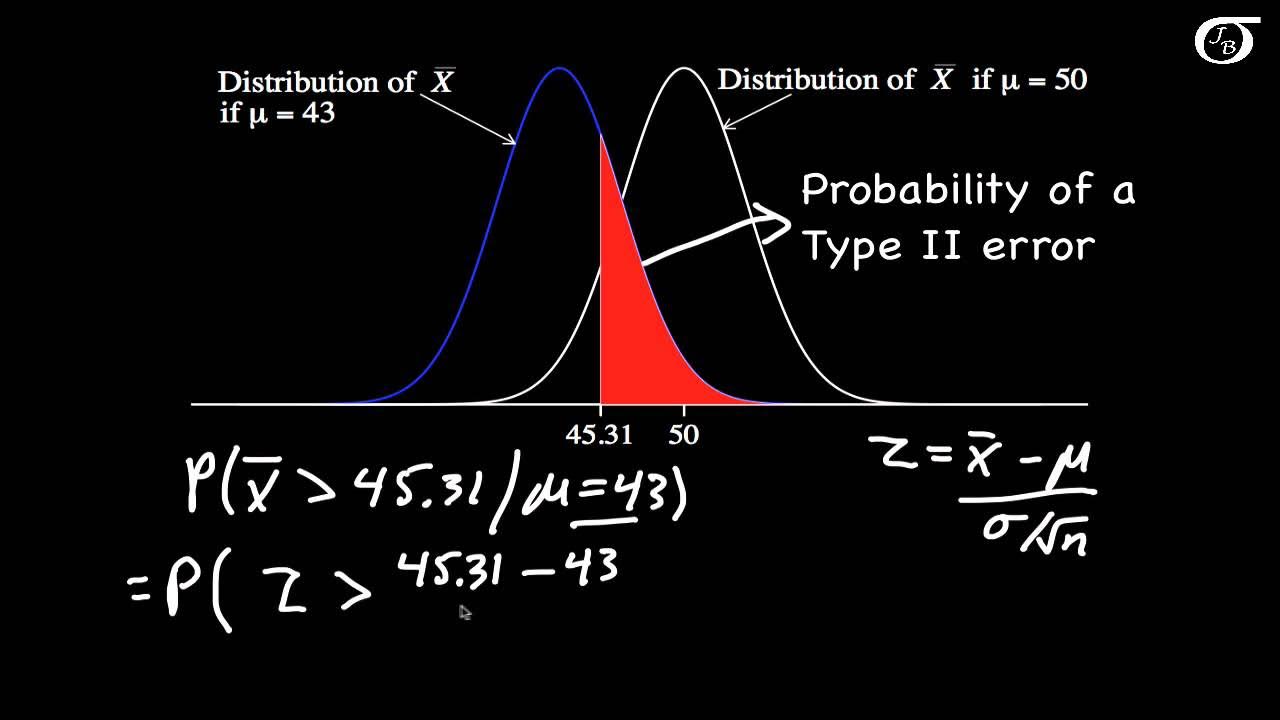
This paragraph introduces the concept of statistical power in the context of a hypothetical medication test aimed at improving typing ability. The average typing speed is stated as 30 words per minute with a standard deviation of 16. The medication is expected to increase this average to 46 words per minute. A sample size of 16 individuals is used to test the medication's efficacy. The concept of power is explained as the probability of correctly rejecting the null hypothesis (which states the mean is 30) when the alternative hypothesis (that the mean is different from 30) is true. The paragraph also explains type 2 error, which is the probability of incorrectly retaining the null hypothesis when it is false. An alpha level of 0.05 is used for the test, and the standard error is calculated to be 4. The paragraph concludes with a visual representation of the distributions under the null and alternative hypotheses and explains how power is the area under the alternative hypothesis distribution that exceeds the critical value determined by the alpha level.

05:01
πŸ“Š Calculating Power and Type 2 Error in Hypothetical Medication Test

This paragraph delves into the calculation of statistical power and type 2 error for the medication test scenario described earlier. It begins by calculating the z-score for the test, using the critical value of 1.96 from the standard normal distribution when the null hypothesis is true. The z-score is calculated by taking the difference between the expected mean under the alternative hypothesis (46 words per minute) and the critical value (37.84 words per minute), divided by the standard error (4). This results in a z-score of -2.04. The paragraph then describes how to use a z-table to find the area in the tail corresponding to this z-score, which represents the power of the test (the probability of correctly rejecting the null hypothesis). The power is found to be approximately 98%, meaning there is a high likelihood that the test will correctly identify the medication as effective. The type 2 error, or beta, is the complement of power, indicating the probability of failing to reject the null hypothesis when it is false, which in this case is about 2%.

Mindmap
Keywords
πŸ’‘Power
In the context of the video, 'power' refers to the statistical power of a hypothesis test, which is the probability that the test will correctly reject the null hypothesis when the alternative hypothesis is true. This is a crucial concept in hypothesis testing as it measures the test's ability to detect an effect when there is one. The video uses the example of a medication that may increase typing ability and explains how power is calculated to determine the likelihood of correctly concluding that the medication is effective.
πŸ’‘Null Hypothesis
The 'null hypothesis' is a fundamental concept in statistical testing. It is a statement of no effect or no difference that is tested with data. In the video, the null hypothesis is that the average typing speed is 30 words per minute, and the test aims to determine if there is enough evidence to reject this assumption in favor of the alternative hypothesis that the medication increases typing speed.
πŸ’‘Alternative Hypothesis
The 'alternative hypothesis' is a statement that is contrary to the null hypothesis and is what researchers typically believe or are trying to prove. In the video, the alternative hypothesis is that the medication does improve typing ability, suggesting that the average words per minute typed are different from 30, specifically increased to 46.
πŸ’‘Type I Error
A 'Type I error' occurs when the null hypothesis is incorrectly rejected when it is actually true. In other words, it's the mistake of concluding there is an effect when there isn't one. The video explains this concept in the context of the medication test, where incorrectly concluding that the medication works would be a Type I error.
πŸ’‘Type II Error
A 'Type II error' happens when the null hypothesis is not rejected when it is actually false. This means failing to detect an effect that is present. The video script refers to Type II error as 'beta' and explains it in the context of the medication test, where not rejecting the null hypothesis when the medication actually does improve typing speed would be a Type II error.
πŸ’‘Standard Deviation
The 'standard deviation' is a measure of the amount of variation or dispersion in a set of values. In the video, the standard deviation of 16 words per minute for typing speed is used to calculate the standard error, which is essential for determining the statistical significance of the test results.
πŸ’‘Sample Size
'Sample size' refers to the number of observations or elements in a sample used for statistical analysis. In the video, a sample size of 16 individuals is taken to test the medication's effect on typing ability. The sample size is important as it affects the power of the statistical test and the precision of the estimates.
πŸ’‘Standard Error
The 'standard error' is the standard deviation of the sampling distribution of a statistic. In the video, the standard error is calculated by dividing the standard deviation by the square root of the sample size. It is used to construct confidence intervals and test statistics, playing a key role in hypothesis testing.
πŸ’‘Alpha Level
The 'alpha level' is the probability threshold for rejecting the null hypothesis and is often set at 0.05 in statistical testing. In the video, an alpha level of 0.05 is used, which means there is a 5% risk of committing a Type I error. The alpha level helps determine the critical values that define the rejection region for the test.
πŸ’‘Z-Score
A 'z-score' represents the number of standard deviations a data point is from the mean of a distribution. In the video, the z-score is calculated to find the value that corresponds to 1.96 standard errors from the mean in the alternative distribution. This helps in determining the probabilities associated with the test results and the power of the test.
πŸ’‘Hypothesis Testing
Hypothesis testing is a statistical method used to make decisions about populations based on sample data. In the video, hypothesis testing is used to evaluate the effectiveness of the medication on typing ability. The process involves setting up a null and alternative hypothesis, calculating test statistics, determining the p-value, and making a decision to reject or not reject the null hypothesis based on the alpha level.
Highlights

Explains the concept of power in statistical testing using an example of a medication that claims to improve typing ability

The average person types at 30 words per minute with a standard deviation of 16

The medication is expected to increase average words per minute typed to 46

A sample of 16 individuals is taken to determine if the medication improves typing ability

Assumes the medication works and the null hypothesis is false while the alternative hypothesis is true

Power is the probability of correctly rejecting the null hypothesis when it is false

Beta is the probability of incorrectly retaining the null hypothesis when it is false

Uses an alpha level of 0.05 for the statistical test

Calculates the standard error as the standard deviation divided by the square root of the sample size

Finds a standard error of 4 for the given example

Shows how to plot the distribution if the null hypothesis is true with a mean of 30 and standard error of 4

Uses an alpha level of 0.05 to determine the critical values of 1.96

Plots a second distribution if the null hypothesis is false with a mean of 46 and standard error of 4

The large orange area in the second distribution represents the power of the test

Calculates the value associated with 1.96 standard errors from the mean in the second distribution

Finds that 1.96 standard errors corresponds to a value of 37.84 in the second distribution

Calculates the z-score to determine the probabilities associated with power and the type 2 error

Looks up the z-score of -2.04 in a standard normal table to find the area in the tail

Finds that the power is about 98% and the type 2 error rate is 2%

Power represents the probability of correctly rejecting the null hypothesis when it is false

The type 2 error rate, or beta, is the probability of not rejecting the null hypothesis when it is false

Transcripts

Browse More Related Video

Calculating Power and the Probability of a Type II Error (A One-Tailed Example)

Introduction to Type I and Type II errors | AP Statistics | Khan Academy

Introduction to power in significance tests | AP Statistics | Khan Academy

8.1.2 Basics of Hypothesis Testing - Significance Level, Type I and Type II Error

Type 1 errors | Inferential statistics | Probability and Statistics | Khan Academy

Errors and Power in Hypothesis Testing | Statistics Tutorial #16 | MarinStatsLectures

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Statistical PowerHypothesis TestingType I ErrorType II ErrorSample SizeStandard DeviationMean CalculationZ-ScoreProbabilityTesting Medication