Are You an Electrician? These are 5 Formulas You Should Know!
TLDRThe video script offers a comprehensive guide for electricians, detailing essential formulas for electrical calculations. It begins with Ohm's Law, explaining its three forms for calculating voltage, current, and resistance. The script then delves into Joule's Law for power calculations, emphasizing the importance of time in energy transfer. Voltage drop, series and parallel resistance calculations, and their impact on electrical systems are also covered. Finally, the script discusses the conversion of watts to horsepower, considering motor efficiency and power factor, with examples for both single-phase and three-phase systems. This informative guide is crucial for electricians to understand and apply these formulas in real-world scenarios.
Takeaways
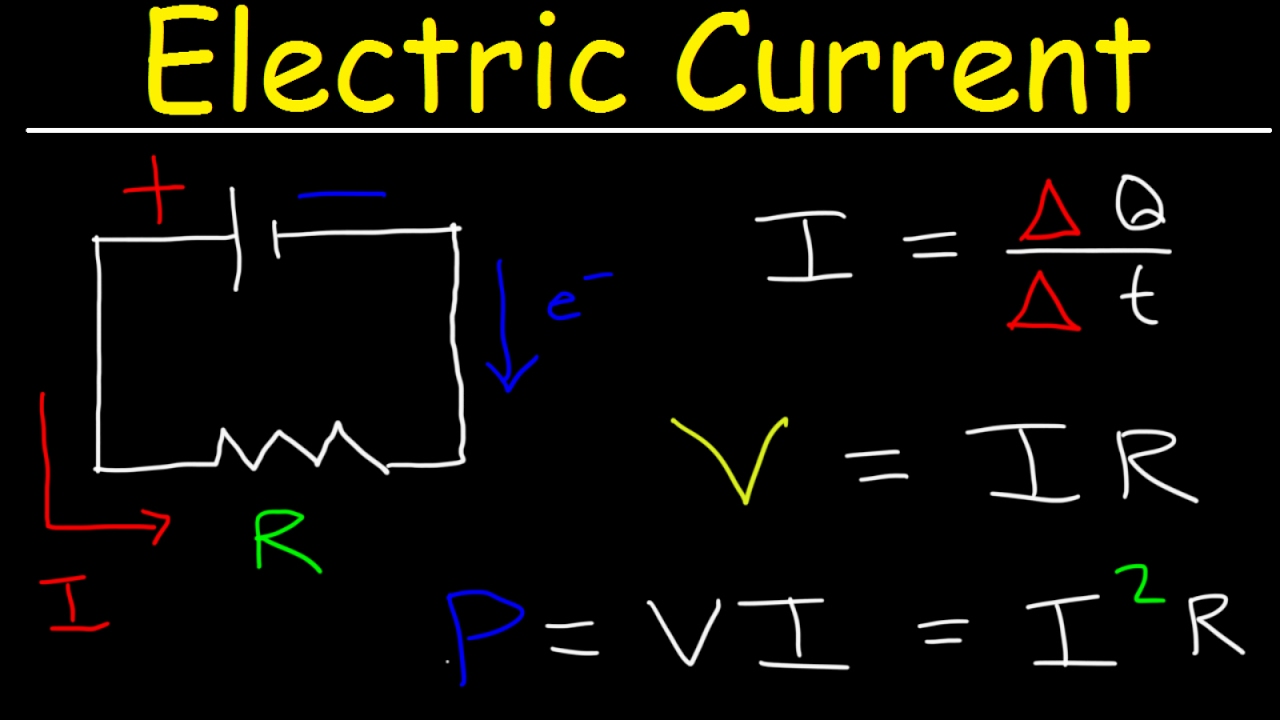
- 📚 Ohm's Law (E=I*R) is fundamental for electricians, relating voltage, current, and resistance.
- 🔌 There are three forms of Ohm's Law: E=I*R for voltage, I=E/R for current, and R=E/I for resistance.
- 💡 Power (P) is the transfer of energy and is calculated using the formula P=I*V, where P stands for power in watts.
- 🌡 Voltage drop is a common occurrence in electrical work and can be estimated using Ohm's law or more accurate voltage drop formulas.
- 🏎️ Conductor materials affect voltage drop; copper has a K factor of 12.9, while aluminum has a K factor of 21.2.
- 📏 The cross-sectional area of a conductor, measured in circular mills, affects its resistance and voltage drop.
- 🔍 Calculating series resistance involves summing the resistance values, while parallel resistance requires the reciprocal of the sum of the reciprocals.
- 🔌 The total resistance in a series circuit is the sum of all individual resistances (RT = R1 + R2 + R3 ...).
- ⚙️ In a parallel circuit, the total resistance is found by taking the reciprocal of the sum of the reciprocals of individual resistances (1/RT = 1/R1 + 1/R2 + 1/R3 ...).
- 🐎 Horsepower (HP) can be converted to watts (1 HP ≈ 746 Watts) and is influenced by motor efficiency and power factor.
- 🔧 When sizing conductors or calculating amperage, refer to the National Electrical Code (NEC) sections 247, 248, 249, and 250.
Q & A
What is Ohm's Law and how is it applied in electrical work?
-Ohm's Law is a fundamental principle in electrical engineering that defines the relationship between voltage (V), current (I), and resistance (R). It is expressed as V = I * R. This law is crucial for electricians as it helps in understanding how electrical systems work and in calculating unknown values in a circuit when the other two are known.
How can you calculate power (P) in an electrical circuit?
-Power in an electrical circuit can be calculated using the formula P = I * V, where P stands for power in watts, I is the current in amperes, and V is the voltage in volts. This formula is derived from the concept of power as the rate at which electrical energy is transferred or converted.
What is the significance of Joule's Law in electrical systems?
-Joule's Law is important for understanding the amount of energy produced or transferred in an electrical system. It states that the energy (in joules) transferred over time is equal to the product of the square of the current, the resistance, and the time interval. This law is crucial in calculating heat generation in circuits and the efficiency of energy conversion in electrical devices.
How do you calculate voltage drop in a circuit?
-Voltage drop can be calculated using the formula VD = I * R, where VD is the voltage drop, I is the current in the conductor, and R is the resistance of the conductor. For more accurate calculations, especially in long runs or with varying materials, a more complex formula involving the conductor's length, material's resistivity (K), and the cross-sectional area (in circular mils) is used.
What is the difference between series and parallel resistance and how do you calculate them?
-In a series circuit, resistances add up (RT = R1 + R2 + R3 + ...), increasing the total resistance. In a parallel circuit, the total resistance is found by taking the reciprocal of the sum of the reciprocals of each resistance (1/RT = 1/R1 + 1/R2 + 1/R3 + ...). Parallel circuits effectively decrease total resistance, allowing more current to flow through the circuit.
How is horsepower related to electrical power and how do you convert between them?
-Horsepower (HP) is a unit of power that, in the context of electricity, is related to the rate at which electrical energy is converted into mechanical energy. One horsepower is approximately equal to 746 watts. To convert electrical power to horsepower, you can use the formula HP = (Power in watts) / 746.
What factors affect the output of a motor in terms of horsepower?
-The output of a motor in terms of horsepower can be affected by several factors including the motor's efficiency rating, the power factor of the circuit, and the actual electrical conditions such as voltage and current. These factors need to be taken into account when calculating the true horsepower output of a motor in an electrical system.
What is the significance of power factor in electrical systems?
-Power factor (PF) is a measure of how effectively the current and voltage are in phase in an AC circuit, which affects the efficiency of power delivery. A power factor of 1 (or 100%) indicates perfect phase alignment and maximum efficiency. A lower power factor indicates a phase lag, which can result in wasted energy and reduced efficiency.
How does the number of conductors affect voltage drop in a circuit?
-The number of conductors can affect voltage drop in a circuit. For instance, in the case of a single-phase circuit, there are typically two conductors (one for the hot wire and one for the neutral), while in a three-phase circuit, there are three conductors. The voltage drop formula for a three-phase circuit includes a factor of 1.732, which accounts for the square root of three, reflecting the nature of three-phase systems and leading to a slightly lower voltage drop compared to single-phase systems with the same current and conductor material.
What are the units used to measure the cross-sectional area of a conductor?
-The cross-sectional area of a conductor is typically measured in circular mils (MCM). One circular mil is the area of a circle with a diameter of one thousandth of an inch (0.001 inches). This unit is used to calculate the resistance and voltage drop in a circuit and is crucial for determining the correct conductor size for a given current load.
How do different materials affect the voltage drop in a circuit?
-Different materials have different resistivities, which affects the voltage drop in a circuit. For example, copper has a lower resistivity than aluminum, meaning that for the same size conductor, a copper wire will have less voltage drop than an aluminum wire. This is why the constant K used in voltage drop calculations is different for copper (12.9) and aluminum (21.2).
What is the role of capacitance in electrical circuits?
-Capacitance plays a significant role in electrical circuits, especially in AC systems. Capacitors store and release electrical energy, which can affect the overall performance of the circuit. In series circuits, the total capacitance is the sum of individual capacitances, while in parallel circuits, the total capacitance is derived from the reciprocal of the sum of the reciprocals of the individual capacitances. Capacitance can help in filtering, timing, voltage regulation, and energy storage within a circuit.
Outlines
🔌 Ohm's Law and Electrical Power
This paragraph introduces the fundamental concepts of Ohm's Law and electrical power, emphasizing the importance of understanding the relationship between voltage, amperage, and resistance. It explains how Ohm's Law can be rearranged to solve for any of these variables and highlights the concept of power in terms of joules. The paragraph also touches on the calculation of power (watts) and how it relates to electrical circuits, including the use of formulas to determine total wattage and current draw in a circuit. The concept of voltage drop is introduced, with an explanation of how it can be calculated using Ohm's Law and the importance of accurate voltage drop calculations in electrical work.
🌐 Voltage Drop and Conductor Properties
The second paragraph delves deeper into voltage drop, explaining the formula and variables involved in calculating it for both single-phase and three-phase circuits. It discusses the significance of conductor material, such as copper and aluminum, and their respective conductivities and resistances. The concept of circular mils as a unit of measurement for the cross-sectional area of a conductor is introduced, along with specific values for common conductor sizes. The paragraph also provides an example calculation for voltage drop, illustrating how to use the formula and the importance of understanding these calculations for practical electrical applications.
🔄 Series and Parallel Resistance Calculations
This paragraph focuses on the methods for calculating total resistance in series and parallel circuits. It clearly explains the straightforward addition method for series circuits and the more complex inverse sum method for parallel circuits. The paragraph also introduces an alternative method for parallel resistance calculation using the product over sum, providing a simpler approach for those familiar with the necessary mathematical operations. The differences in resistance behavior in series and parallel configurations are highlighted, along with the practical implications for current flow and circuit design.
🏎️ Horsepower and Motor Output Calculation
The final paragraph discusses the calculation of horsepower based on the output of a motor, considering factors such as voltage, amperage, motor efficiency, and power factor. It explains the conversion of watts to horsepower and how to adjust for motor efficiency and power factor in these calculations. The paragraph provides examples for both single-phase and three-phase circuits, demonstrating the impact of these factors on the calculated horsepower. It also touches on the increased power transfer in three-phase circuits compared to single-phase, and the resulting higher horsepower output. The paragraph concludes with a brief mention of more advanced electrical concepts that could be explored for further understanding.
Mindmap
Keywords
💡Ohm's Law
💡Power
💡Joules Law
💡Voltage Drop
💡Conductors
💡Circular Mils
💡Series and Parallel Resistance
💡Horsepower
💡Power Factor
💡Capacitance
💡National Electrical Code (NEC)
Highlights
Ohm's Law is a fundamental concept for electricians, describing the relationship between voltage, amperage, and resistance.
Ohm's Law can be structured in three different ways (E=IR, I=E/R, R=E/I) for solving different electrical parameters.
Power, measured in joules, represents the transfer of energy from one system to another, such as electrical energy being converted to light and heat in a bulb.
Joule's Law (P=IE) is used to calculate power in electrical circuits, where P is power in watts, I is current in amperes, and E is voltage in volts.
Voltage drop is a common occurrence in electrical fields, which can be estimated using Ohm's Law or more accurate voltage drop formulas.
The voltage drop formula accounts for factors such as conductor material (copper or aluminum), length, amperage, and the cross-sectional area of the conductor.
Series and parallel resistance calculations yield different total resistance values, with series circuits adding resistances and parallel circuits involving the inverse of the sum of inverses.
Horsepower can be converted to watts, with 1 horsepower approximately equal to 746 watts, and is used to determine the output of a motor.
Motor efficiency and power factor are crucial factors affecting the true horsepower output of a motor.
Three-phase circuits and motors typically provide greater power transfer and efficiency compared to single-phase systems.
The National Electrical Code (NEC) provides guidelines for sizing conductors and calculating amperage for various electrical setups.
Capacitance and inductive reactance are additional electrical concepts that can be explored for more complex circuit analysis.
Trigonometry and calculus can also play a role in advanced electrical theory and circuit analysis.
Electricians should be familiar with these formulas and concepts to perform their tasks effectively and safely.
The video provides a comprehensive overview of essential electrical formulas and their practical applications in the field.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: