Ohm's Law
TLDRThis video script offers a comprehensive explanation of Ohm's law, detailing its relationship with voltage, current, and resistance. It walks through a practice problem involving a 12-volt battery and a four-ohm resistor, then extends the discussion to series and parallel circuits, demonstrating how total resistance and voltage drops across resistors are calculated. The script also introduces Kirchhoff's voltage and current laws, emphasizing their importance in understanding energy conservation and current distribution in circuits. The content is presented in a clear, step-by-step manner, making it accessible for learners to grasp the fundamental concepts of electrical circuits.
Takeaways
- 📜 Ohm's Law defines the relationship between voltage (V), current (I), and resistance (R) with the formula V = IR.
- 🔋 Voltage and current are directly proportional when resistance is constant, meaning an increase in voltage leads to an increase in current.
- ⚙️ Resistance and current are inversely related; as resistance increases, current decreases if voltage is held constant.
- 🔌 In a series circuit, the current is the same through all resistors, but the voltage drop across each resistor depends on its resistance value.
- 🔄 Kirchhoff's Voltage Law states that the sum of all voltages in a closed loop equals zero, reflecting energy conservation in a circuit.
- 🔌 In a parallel circuit, the voltage across each resistor is the same, but the current through each resistor may differ based on its resistance.
- 📈 The total current leaving the power source in a parallel circuit is the sum of the currents through each branch.
- 🔄 Kirchhoff's Current Law states that the current entering a junction equals the current leaving it, which helps in analyzing branched circuits.
- 📊 The voltage drop across a resistor in a series circuit can be calculated using Ohm's Law (V = IR) with the specific resistance and current through that resistor.
- 🔧 When resistors are connected in series, the total resistance is the sum of individual resistances, affecting the overall current in the circuit.
- 🔩 When resistors are connected in parallel, the reciprocal of the total resistance is the sum of the reciprocals of the individual resistances, which affects the current distribution.
- 🎥 The video provides practical examples of applying Ohm's Law and Kirchhoff's Laws to analyze series and parallel circuits, enhancing understanding of basic electrical principles.
Q & A
What is Ohm's law and how does it relate voltage, current, and resistance?
-Ohm's law is a fundamental principle in electrical engineering that states the relationship between voltage (V), current (I), and resistance (R). It is expressed by the formula V = I * R, where V represents voltage in volts, I is the current in amps, and R is the resistance in ohms. This law shows that the voltage across a conductor is directly proportional to the current flowing through it and inversely proportional to its resistance.
How does the current change in a circuit when the voltage is increased, assuming resistance remains constant?
-If the voltage in a circuit is increased while the resistance remains constant, the current will increase proportionally. This is because, according to Ohm's law (V = I * R), if V increases and R stays the same, I must also increase to maintain the equality.
What happens to the current when resistance increases in a circuit with a constant voltage?
-In a circuit with a constant voltage, if the resistance increases, the current will decrease. This is due to the inverse relationship between current and resistance as described by Ohm's law (V = I * R). If R increases and V remains constant, I must decrease to satisfy the equation.
How do you calculate the total resistance in a series circuit?
-In a series circuit, the total resistance (R_total) is the sum of all individual resistances (R1, R2, R3, etc.). To calculate it, you simply add up the values of each resistor in series: R_total = R1 + R2 + R3 + ...
What is Kirchhoff's voltage law and how does it apply to a closed loop?
-Kirchhoff's voltage law states that the algebraic sum of all the voltages (both increases and decreases) around a closed loop in a circuit is always zero. This makes sense because the energy supplied by the battery (positive voltage) must be equal to the energy consumed by the resistors (negative voltage drops). The law ensures the conservation of energy in the circuit.
How does the current differ in a parallel circuit compared to a series circuit?
-In a series circuit, the current is the same through all resistors because there is only one path for the current to flow. However, in a parallel circuit, the current can divide among multiple paths, and each path can have a different current depending on the resistance of that path. The voltage across each resistor in a parallel circuit is the same, though, because they are all directly connected to the voltage source.
How do you calculate the current flowing through each resistor in a parallel circuit?
-In a parallel circuit, you use Ohm's law (V = I * R) to calculate the current through each resistor individually. You divide the voltage across the resistor (which is the same as the voltage of the source) by the resistance of each resistor to find the current flowing through it: I = V / R. Each resistor will have a different current if their resistances are different.
What is the total current that leaves the battery in a parallel circuit?
-In a parallel circuit, the total current that leaves the battery (I_total) is the sum of the currents flowing through each resistor. If you have currents I1, I2, I3, etc., through resistors R1, R2, R3, etc., then the total current from the battery is I_total = I1 + I2 + I3 + ...
What is Kirchhoff's current law and how does it apply to a junction in a circuit?
-Kirchhoff's current law states that the total current entering a junction (or node) in a circuit is equal to the total current leaving the junction. This law is based on the principle of conservation of charge, which says that charge can neither be created nor destroyed. It is used to analyze complex circuits and determine the current flowing through specific branches.
How does the current distribution in a parallel circuit depend on the resistance values?
-In a parallel circuit, the current distribution among the branches depends inversely on the resistance values. Lower resistance values will have higher currents, and higher resistance values will have lower currents, assuming the same voltage across all resistors. This is because the current prefers to flow through paths of lower resistance.
What is the sum of voltage drops across resistors in a series circuit?
-In a series circuit, the sum of the voltage drops across each resistor is equal to the total voltage supplied by the battery. This is because the voltage across each resistor (V1, V2, V3, etc.) is the product of the current flowing through it and its resistance (Ohm's law), and since the current is the same through all resistors in series, the sum of these voltage drops (V1 + V2 + V3 + ...) equals the battery voltage.
Outlines
📚 Introduction to Ohm's Law
This paragraph introduces the fundamental concepts of Ohm's Law, explaining its role in describing the relationship between voltage, current, and resistance. The equation V=IR is presented, with V representing voltage, I for current, and R for resistance. The units for these quantities are volts, amps, and ohms, respectively. The paragraph further discusses the proportional relationship between voltage and current, and the inverse relationship between current and resistance, given a constant voltage. A practical problem is presented, involving a 12-volt battery and a 4-ohm resistor, and the use of Ohm's Law to calculate the resulting current.
🔍 Series Circuit Analysis
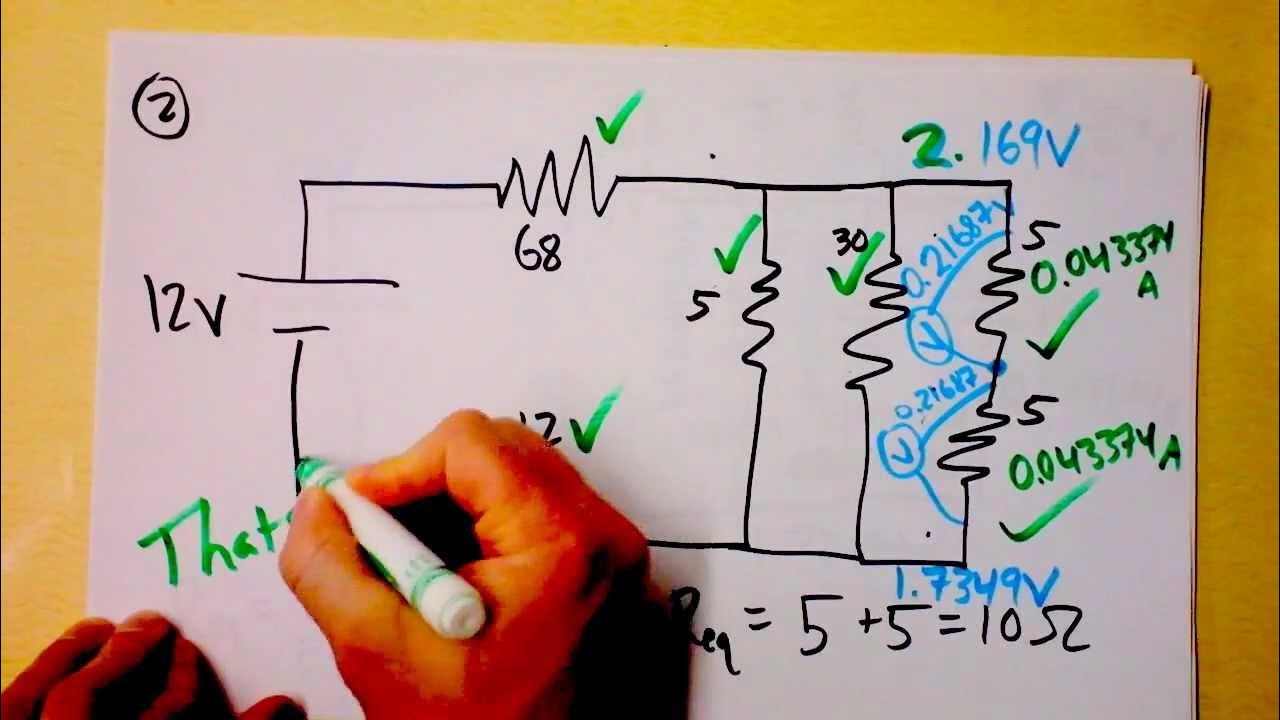
This paragraph delves into the specifics of analyzing series circuits, where resistors are connected one after another. It explains how the total resistance in a series circuit is the sum of the individual resistances. Using a 60-volt battery and three resistors with values of 3 ohms, 4 ohms, and 5 ohms as an example, the paragraph demonstrates how to calculate the current flowing through the circuit. It also shows how to determine the voltage drop across each resistor by applying Ohm's Law in reverse. The concept of Kirchhoff's Voltage Law is introduced, stating that the total voltage around a loop in a circuit must be zero, reflecting the conservation of energy.
🌐 Parallel Circuit Exploration
The paragraph explores the behavior of parallel circuits, where resistors are connected in multiple paths. It contrasts this with series circuits, noting that while the current is the same through all resistors in series, it can vary in a parallel circuit. The voltage across each resistor in parallel is the same, as provided by the battery. The paragraph uses a 12-volt battery and three resistors with values of 3 ohms, 4 ohms, and 6 ohms to calculate the current through each resistor. It highlights the inverse relationship between resistance and current, with lower resistances allowing more current to flow. The total current leaving the battery is determined by summing the individual currents through each resistor, demonstrating the application of Kirchhoff's Current Law, which states that the current entering a junction equals the current leaving it.
Mindmap
Keywords
💡Ohm's Law
💡Voltage
💡Current
💡Resistance
💡Series Circuit
💡Parallel Circuit
💡Voltage Drop
💡Kirchhoff's Voltage Law
💡Kirchhoff's Current Law
💡Practice Problem
💡Circuit Analysis
Highlights
Ohm's law describes the relationship between voltage, current, and resistance.
The equation for Ohm's law is V = I * R, where V stands for voltage, I for current, and R for resistance.
Voltage is measured in volts, current in amps, and resistance in ohms.
As the voltage in a circuit increases, the current will increase, provided that the resistance stays the same.
If the resistance increases while the voltage is constant, the current will decrease.
Voltage and current are proportional to each other, and resistance and current are inversely related.
In a series circuit, the current flowing through resistors is the same because there's only one path for the current to flow.
In a parallel circuit, the voltage across resistors is the same, but the current can vary as it has multiple paths.
Kirchhoff's voltage law states that as you go around a circuit in a loop, the total voltage will be zero.
Kirchhoff's current law states that the current that enters a junction is equal to the current that leaves the junction.
In a series circuit, the total resistance is the sum of the individual resistances.
In a parallel circuit, the current flowing through each resistor can be calculated using Ohm's law with the individual resistances.
The total current in a parallel circuit is the sum of the individual currents through each resistor.
The voltage drop across a resistor in a series circuit can be calculated using Ohm's law with the current flowing through that resistor.
The sum of all the voltage drops across resistors in a series circuit equals the voltage of the battery.
The current flowing through a resistor in a parallel circuit is inversely related to its resistance.
The battery supplies energy to the circuit, while resistors consume energy, resulting in a net energy balance according to Kirchhoff's laws.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: