Improper Integrals - Convergent or Divergent (Made Easy)
TLDRThis educational video dives into the intriguing world of improper integrals, specifically those that extend to infinity. It begins by defining convergent and divergent integrals, illustrating how to determine the convergence of an integral through examples. The video thoroughly explains the process of converting improper integrals into limits, using the second fundamental theorem of calculus, and demonstrates solving these limits to determine convergence or divergence. Several examples, including integrals of 1/x^p, x*e^x, and 1/(x^2+1), are worked through, highlighting techniques like integration by parts and L'Hôpital's rule. The presentation culminates in showing how to handle integrals with discontinuities within the interval, providing viewers with a comprehensive guide on solving and understanding improper integrals.
Takeaways
- 💡 An improper integral involves infinity either in its interval of integration or its integrand approaching a singularity within the integration limits.
- 🔮 Convergence of an improper integral occurs when it results in a finite number, whereas divergence is indicated by an infinite result.
- 📖 The process to solve improper integrals often involves converting them into limits as a variable (commonly t) approaches infinity or a point of discontinuity.
- 📚 Utilizing the Second Fundamental Theorem of Calculus allows the transformation of an improper integral into a limit problem involving definite integrals.
- 🎲 For 1/x^p type integrals from 1 to infinity, convergence or divergence is determined by the value of p: convergent if p > 1, divergent if p ≤ 1.
- 🔨 Integration by parts is a useful technique for solving integrals involving products of functions, guided by the LIATE rule.
- 📝 L'Hôpital's Rule can address indeterminate forms encountered when evaluating limits within the process of solving improper integrals.
- 📈 The integral of 1/(x^2 + 1) from negative to positive infinity is convergent and can be evaluated by splitting the integral at any point, commonly 0, then solving each part.
- 🛠 Presence of a singularity within the integration limits, such as a division by zero, classifies an integral as improper, requiring special methods to solve.
- 🎱 An improper integral with a singularity at a point involves approaching the point from the left or right in the limit, and its convergence depends on the behavior of the function near the singularity.
Q & A
What is an improper integral?
-An improper integral is an integral that has an infinite limit of integration, such as an integral from 1 to infinity or from negative infinity to infinity. These types of integrals can be convergent or divergent depending on the function being integrated and the limits involved.
How do you determine if an integral is convergent or divergent?
-To determine if an integral is convergent or divergent, you need to evaluate the integral and see if it results in a finite number or infinity. If the result is a finite number, the integral is convergent; if the result is infinity, the integral is divergent.
What is the first step in solving an improper integral?
-The first step in solving an improper integral is to convert the integral into a limit. This involves replacing the infinite limit with a variable, such as 't', and then taking the limit as 't' approaches infinity or negative infinity, depending on the context.
What is the second fundamental theorem of calculus used for in the context of improper integrals?
-The second fundamental theorem of calculus is used to evaluate improper integrals by allowing us to express the integral in terms of a limit of a function. Specifically, it states that the integral of a function from 'a' to 't' can be expressed as the limit as 't' approaches 'a' of the function 'f(t)' minus 'f(a)', where 'f(t)' is the antiderivative of the function being integrated.
How do you find the antiderivative of 1/x^2?
-The antiderivative of 1/x^2 is found by using the power rule for integration. Specifically, the integral of x to the power of -2 is the antiderivative, which is -1/x plus a constant (C). So, the antiderivative is -1/x + C.
What is the significance of the p-test in evaluating improper integrals?
-The p-test is a useful tool for determining the convergence or divergence of certain improper integrals of the form ∫ from 1 to infinity of 1/x^p dx. If p > 1, the integral converges, and if p ≤ 1, the integral diverges. This test helps to quickly assess the behavior of such integrals without having to evaluate the integral fully.
What is integration by parts and how is it used in solving improper integrals?
-Integration by parts is a technique used to integrate a product of two functions. The formula for integration by parts is ∫u dv = uv - ∫v du. It is used in solving improper integrals when the integral involves a product of the function and its derivative or an exponential function. By applying integration by parts, you can transform the integral into a more manageable form that can be evaluated as a limit.
What is L'Hôpital's rule and how does it apply to improper integrals?
-L'Hôpital's rule is a method for evaluating limits of the form 0/0 or ∞/∞ by differentiating the numerator and the denominator until a determinate form is obtained. In the context of improper integrals, L'Hôpital's rule can be applied when trying to evaluate limits of the form ∞ - ∞ or 0/0 that arise from the subtraction or division of exponential functions, allowing us to find a determinate value for the integral.
How do you split an improper integral that has a discontinuity within its interval?
-To handle an improper integral with a discontinuity, you can split the integral into two parts: one from the lower limit to just before the point of discontinuity, and another from just after the point of discontinuity to the upper limit. Each part is then evaluated as a limit, and if one of the limits is infinite, the entire integral is considered divergent.
What happens when you encounter a discontinuity within the interval of an improper integral?
-When a discontinuity is encountered within the interval of an improper integral, the integral must be split at the point of discontinuity. Each resulting integral is then evaluated separately as a limit. If any of the resulting limits is infinite, the original integral is considered divergent.
What is the significance of the graph of a function in evaluating improper integrals?
-The graph of a function can provide visual insights into the behavior of the function as it approaches the limits of integration in an improper integral. By observing the graph, you can determine whether the function approaches infinity, zero, or some other value, which can help in predicting whether the integral is convergent or divergent.
How can you use the concept of horizontal asymptotes to evaluate improper integrals?
-Horizontal asymptotes can be used to determine the convergence or divergence of improper integrals. If a function has a horizontal asymptote, the integral can be evaluated by considering the limit of the function as it approaches the asymptote. This can help in evaluating the area under the curve as the limits of integration approach infinity or negative infinity.
Outlines
📚 Introduction to Solving Improper Integrals
This paragraph introduces the concept of improper integrals and the criteria for determining if an integral is convergent or divergent. An integral is considered convergent if its result is a finite number, and divergent if the result is infinite. The process of solving improper integrals involves converting the integral into a limit, utilizing the fundamental theorem of calculus, and finding the antiderivative of the integrand. The explanation includes a step-by-step solution of a specific improper integral and demonstrates how to determine its convergence by evaluating the limit as it approaches infinity.
📈 Divergence and Convergence of Integral Functions
This paragraph delves into the analysis of integral functions and their graphical representations to determine if they diverge or converge. It explains how to identify divergent integrals by observing the behavior of their functions as they approach infinity. The paragraph also presents a method for solving convergent integrals using integration by parts and applying L'Hopital's rule to evaluate limits involving indeterminate forms. The explanation includes solving two different integrals, one divergent and one convergent, and highlights the importance of recognizing the value of p in the integral formula to determine convergence.
📊 Splitting Integrals and Applying Limits
This paragraph discusses the technique of splitting integrals to simplify the process of solving improper integrals. It explains how to break down an integral into manageable parts, especially when the integrand causes division by zero or approaches infinity. The paragraph provides a detailed solution for an integral that involves the natural logarithm and the arctangent function, showcasing the use of limits and the properties of their graphs to find the value of the integral. It emphasizes the significance of splitting integrals at points where the integrand becomes undefined to maintain the convergence of the overall integral.
🔢 Solving Improper Integrals with Division by Zero
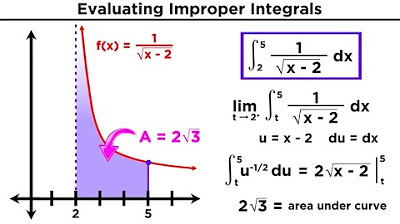
This paragraph focuses on improper integrals that involve division by zero within their range. It explains the method of splitting the integral at the point of division by zero and solving each part separately. The paragraph provides a step-by-step solution for an integral that is improper due to division by zero at a specific point within its domain. It illustrates the use of substitution and the application of limits to find the value of the integral. The explanation also touches on the concept of absolute value and its role in determining the convergence or divergence of the integral.
🎓 Summary and Homework Assignment
The final paragraph summarizes the key concepts and techniques learned in the video script about improper integrals. It reiterates the importance of determining the convergence or divergence of integrals and the methods used to evaluate them. The paragraph concludes with a homework assignment, suggesting a similar integral problem for practice that could potentially appear on a test. The assignment aims to reinforce the understanding of improper integrals and the application of the concepts learned throughout the video.
Mindmap
Keywords
💡Improper Integrals
💡Convergence
💡Divergence
💡Limits
💡Fundamental Theorem of Calculus
💡Antiderivatives
💡Integration by Parts
💡L'Hopital's Rule
💡Trigonometric Functions
💡Graphing Functions
💡Substitution Method
Highlights
The video explains how to solve improper integrals, which have an infinity on the integral sign.
An integral is convergent if the result is a number and divergent if the result is infinity.
The first step in solving an improper integral is to convert it into a limit.
The second fundamental theorem of calculus is used to rewrite the integral in terms of a limit of a function.
The integral of 1/x^2 can be rewritten as the integral of x^(-2), and its anti-derivative is 1/x.
The limit of the function 1/x as x approaches infinity is zero, indicating the integral is convergent.
The integral from 1 to infinity of 1/x is divergent, as the limit of the function ln(x) as x approaches infinity is infinity.
A formula is provided to determine the convergence of an integral from 1 to infinity of 1/x^p if p is larger than 1, it's convergent; if p is smaller or equal to 1, it's divergent.
Integration by parts is used for the integral from negative infinity to 0 of x*e^x dx, with u = x and dv = e^x dx.
The anti-derivative of x*e^x is x*e^x - e^x + C, and the limit as t approaches negative infinity of this expression is negative one.
The integral from negative infinity to positive infinity of 1/(x^2+1) is convergent and can be split into two integrals for easier calculation.
The anti-derivative of 1/(x^2+1) is arctan(x), and the limit as t approaches negative infinity is negative pi/2, indicating convergence.
Improper integrals can also arise when the function has a discontinuity, such as dividing by zero.
The integral from 0 to 3 of 1/(x-1) is improper due to division by zero at x=1 and is split into two integrals to solve.
The limit as t approaches 1 from the left of the integral from 0 to t of 1/(x-1) is negative infinity, indicating the integral is divergent.
The video provides a comprehensive guide on solving various types of improper integrals, including those with infinite limits and discontinuities.
The video concludes with a homework problem, the integral from 0 to 1 of ln(x) dx, which is convergent with a solution of negative 1.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: