Improper Integrals - Convergence and Divergence - Calculus 2

The Organic Chemistry Tutor
26 Jan 202113:55
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the evaluation of improper integrals, emphasizing the concept of convergence and divergence. It illustrates the process with examples, including the integral of 1/x from 1 to infinity, which diverges, and the integral of 1/x^2 from 1 to infinity, which converges to 1. The p-series is introduced as a guideline for determining the convergence of improper integrals, with p > 1 indicating convergence and p ≤ 1 indicating divergence. The script also demonstrates the use of substitution and limits to evaluate more complex integrals, reinforcing the fundamental theorem of calculus.

Takeaways
  • 📌 The concept of improper integrals is introduced, which involves calculating integrals with infinite limits.
  • 🔍 To evaluate an improper integral, replace infinity with a variable (e.g., t) and express the integral as a limit.
  • 🌟 If the limit of the integral exists and is finite, the integral converges; if not, it diverges.
  • 📈 The first example involves the integral of 1/x from 1 to infinity, which diverges as the limit results in infinity.
  • 📊 The second example is the integral of 1/x^2 from 1 to infinity, which converges to a finite value (+1) as the limit approaches zero.
  • 📚 The p-series is mentioned as a tool to determine the convergence of improper integrals involving 1/x^p, where if p > 1, the integral converges, and if p ≤ 1, it diverges.
  • 🧠 The third example examines the integral of 1/(3x+1)^2 from 1 to infinity, which is similar to the 1/x^2 case and converges to a finite value (1/12).
  • 🎓 U-substitution is used in the third example to find the antiderivative of the integrand, setting u = 3x + 1 and using du/3 = dx.
  • 🔧 The fundamental theorem of calculus is applied to rewrite the improper integral as a limit of the antiderivative evaluated at the bounds.
  • 📐 The process of evaluating limits at infinity and simplifying expressions is crucial for determining the convergence of improper integrals.
  • 📈 The script provides a clear methodology for approaching and solving improper integrals, emphasizing the importance of limits and antiderivatives.
Q & A

  • What is the integral from 1 to infinity of 1 over x dx?

    -This is an improper integral. By replacing infinity with a variable t and taking the limit as t approaches infinity, we find that the integral diverges to infinity because the natural log of infinity is infinity.

  • How do we determine if an improper integral converges or diverges?

    -An improper integral converges if the limit of the integral exists as the infinite limit approaches, resulting in a finite number. If the limit does not exist or results in infinity, the integral diverges.

  • What is the anti-derivative of 1 over x?

    -The anti-derivative of 1 over x is the natural logarithm of x, denoted as ln x.

  • How does the p-series concept relate to improper integrals?

    -The p-series concept is a way to determine the convergence of certain types of improper integrals. If the integral is of the form 1/x^p dx from 1 to infinity and p > 1, the integral converges. If p ≤ 1, the integral diverges.

  • What is the result of the improper integral of 1/x^2 from 1 to infinity?

    -The improper integral of 1/x^2 from 1 to infinity converges to a finite value, which is 1, by applying the p-series rule with p=2, which is greater than 1.

  • How do you evaluate the improper integral of 1/(3x+1)^2 from 1 to infinity?

    -By using u-substitution with u = 3x + 1, the integral becomes 1/(3(u-1)^2) du. After evaluating the limit as the upper limit approaches infinity, the result converges to 1/12.

  • What is the significance of the natural logarithm function in evaluating improper integrals?

    -The natural logarithm function, ln x, is significant in evaluating improper integrals because it provides a way to find the anti-derivative of 1/x, which is crucial in determining the convergence or divergence of such integrals.

  • What happens when you divide by a very large number in the context of improper integrals?

    -When you divide by a very large number, such as infinity, the result approaches zero. This is important in determining the limit of certain improper integrals as the upper limit approaches infinity.

  • How does the fundamental theorem of calculus help in evaluating improper integrals?

    -The fundamental theorem of calculus allows us to rewrite an improper integral as a limit of a definite integral. This helps in evaluating the integral by finding the antiderivative of the function and then applying the limit to the result.

  • What is the role of the limit process in evaluating improper integrals?

    -The limit process is essential in evaluating improper integrals because it allows us to handle the infinite limits by replacing them with a variable and then taking the limit as that variable approaches the infinite value. This process helps us to determine whether the integral converges to a finite number or diverges to infinity.

  • How does the power rule for integration apply to the improper integral of 1/x^2?

    -The power rule for integration is applied by changing the exponent of x in the function 1/x^2 to find the antiderivative. By moving the 2 to the top (with a change in sign) and dividing by the result, we find that the antiderivative is -1/x.

  • What is the value of the improper integral of 1/(3x+1)^2 from 1 to infinity?

    -The value of the improper integral of 1/(3x+1)^2 from 1 to infinity is 1/12. This is determined by applying u-substitution, finding the antiderivative, and evaluating the limit as the upper limit approaches infinity.

Outlines
00:00
📚 Evaluation of Improper Integrals

This paragraph introduces the concept of improper integrals and explains how to evaluate them. The integral from 1 to infinity of 1/x^2 is used as an example to demonstrate the process. It clarifies that if the integral results in a finite number, it converges; if it results in infinity, it diverges. The paragraph walks through the steps of replacing infinity with a variable (t), finding the antiderivative (ln x), and applying the fundamental theorem of calculus to find the limit. The example integral diverges, as the natural log of infinity is infinity.

05:00
📈 Convergence and Divergence of Integrals

The second paragraph delves into the criteria for determining whether an improper integral converges or diverges. It introduces the p-series as a tool for making this determination, explaining that if p > 1, the integral converges, and if p ≤ 1, it diverges. This is illustrated with two examples: the first example (1/x from 1 to ∞) diverges because p=1, while the second example (1/x^2 from 1 to ∞) converges because p=2. The paragraph emphasizes the importance of the p-series in understanding the behavior of improper integrals.

10:02
🔢 Application of u-Substitution in Integration

The third paragraph focuses on the application of u-substitution in evaluating a specific improper integral: 1/(3x+1)^2 from 1 to ∞. It outlines the process of identifying the antiderivative using u-substitution, where u = 3x + 1, and transforming the integral into a form that can be solved. The paragraph then calculates the limit as t approaches infinity, ignoring the constant of integration, and arrives at the final answer of 1/12, indicating that the integral converges. The explanation includes a detailed breakdown of the algebraic manipulations and the rationale behind each step.

Mindmap
Keywords
💡Improper Integral
An improper integral is a type of integral that has one or both limits of integration approaching infinity. In the context of the video, the improper integrals are used to evaluate expressions where the limits of integration are not finite numbers. For example, the integral from 1 to infinity of 1/x dx is an improper integral because the upper limit is infinity.
💡Convergence
In mathematics, convergence refers to the process of a sequence or a series approaching a particular value as the number of terms increases indefinitely. In the context of the video, convergence is used to describe whether an improper integral approaches a finite value. If the integral evaluates to a finite number, it is said to have converged; otherwise, it is divergent.
💡Divergence
Divergence, in the context of improper integrals, indicates that the integral does not approach a finite value. Instead, the value of the integral grows without bound or oscillates infinitely as the limits of integration approach infinity. The video explains that if an improper integral results in infinity, it is divergent.
💡Anti-Derivative
An anti-derivative, also known as an indefinite integral, is a function that represents the area under the curve of a given function. It is the reverse process of differentiation. In the video, finding the anti-derivative is a crucial step in evaluating integrals, as it allows the calculation of the area between the curve and the x-axis over a given interval.
💡Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus is a key concept that connects differentiation and integration. It states that if a function is continuous on a closed interval [a, b] and has an anti-derivative F, then the definite integral of the function over that interval can be computed as F(b) - F(a). In the video, this theorem is used to rewrite limit expressions as integrals and to evaluate them.
💡Limit
In mathematics, a limit is the value that a function or sequence 'approaches' as the input (or index) gets arbitrarily close to a certain point. Limits are used to describe the behavior of functions at points where they are not defined or not continuous, such as at infinity.
💡Power Rule for Integration
The power rule for integration is a fundamental rule in calculus that allows the integration of a function where the variable is raised to a power. According to the rule, the integral of x^n (where n is a constant) is x^(n+1)/(n+1) + C, where C is the constant of integration.
💡u-Substitution
u-Substitution is a technique used in integration to simplify the process by transforming the integrand into a more manageable form. It involves replacing the variable of integration with a new variable (u), and then using the derivative of the new variable to replace the differential (dx).
💡p-Series
The p-Series is a type of infinite series that has the form 1/p, where p is a positive real number. It is used to determine the convergence or divergence of certain improper integrals, with the video explaining that if p > 1, the integral converges, and if p ≤ 1, the integral diverges.
💡Natural Logarithm
The natural logarithm, denoted as ln(x), is the logarithm to the base e (where e is the mathematical constant approximately equal to 2.71828). It is a fundamental concept in calculus and is used to calculate areas under curves, as well as to solve exponential growth and decay problems.
💡Integration by Parts
Integration by parts is a technique used in calculus to integrate a product of two functions. It is based on the product rule for differentiation and involves reversing the process to find the integral. The formula for integration by parts is ∫udv = uv - ∫vdu, where u and dv are functions chosen based on the integrand.
Highlights

Evaluation of the improper integral from 1 to infinity of 1 over x dx.

Determination of convergence or divergence of an integral by checking for a finite number.

Rewriting infinity with a variable t to evaluate improper integrals.

Using the natural logarithm as the antiderivative of 1 over x.

The limit of natural logarithm of t as t approaches infinity results in infinity.

The improper integral from 1 to infinity of 1 over x squared dx is convergent.

The antiderivative of 1 over x squared is negative one over x.

The limit of negative one over t as t approaches infinity is zero, making the integral converge to positive one.

Introduction to the p-series to determine the convergence of improper integrals based on the value of p.

Improper integral is convergent if p is greater than 1 and divergent if p is less than or equal to 1.

Evaluation of the improper integral from 1 to infinity of 1 over (3x + 1) squared dx.

Use of u-substitution with u = 3x + 1 to find the antiderivative.

The antiderivative of 1 over (3x + 1) squared is negative one over three times (3x + 1).

The limit calculation leading to the integral converging to one over twelve.

Demonstration of the limit approaching zero for the term negative one over nine t plus three.

Final answer of the improper integral from 1 to infinity of 1 over (3x + 1) squared dx is one over twelve.

Transcripts

Browse More Related Video

Improper Integrals - Convergent or Divergent (Made Easy)

Improper Integrals BC Calc

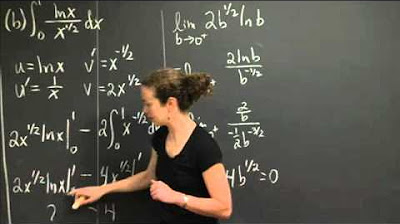
Improper Integrals | MIT 18.01SC Single Variable Calculus, Fall 2010

Improper Integrals - Infinite Bounds

Proof of p-series convergence criteria | Series | AP Calculus BC | Khan Academy

Introduction to improper integrals | AP Calculus BC | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusIntegralsConvergenceDivergentp-SeriesInfinite LimitsMathematicsEducationTutorialImproper Integrals