Improper Integrals - Infinite Bounds

turksvids

8 Jun 201404:39

EducationalLearning

32 Likes 10 Comments

TLDRThis video tutorial delves into improper integrals, focusing on the third type where bounds are infinite. It demonstrates how to evaluate the integral from 0 to infinity of x^2 over 1 + x^3, revealing its divergence. The second example breaks down the integral from negative to positive infinity of 1 over 1 + x^2 into two parts, using the arctan function, and concludes with a finite value of pi. The video is an insightful guide for understanding and solving improper integrals with infinite limits.

Takeaways

📚 There are four types of improper integrals: discontinuities at bounds A or B, a discontinuity between A and B, infinite bounds, and combinations of these.
🔍 The video focuses on the third type of improper integrals where the bounds are infinite, such as from 0 to Infinity or negative Infinity to positive Infinity.
🧐 The first integral example given is from 0 to Infinity of x^2 over (1 + x^3), and it is solved by using a natural logarithm substitution method.
📉 The integral of x^2 over (1 + x^3) diverges, as the natural logarithm of infinity does not converge to a finite value.
📈 The second integral example is from negative Infinity to Infinity of 1 over (1 + x^2), which is split into two parts to handle the infinite bounds.
📚 The integral is solved by recognizing 1/(1 + x^2) as the derivative of arctan(x), and using limits to evaluate the integral over the infinite bounds.
📝 The arctan function has horizontal asymptotes at negative Pi/2 and Pi/2, which are important when evaluating limits at infinity.
🔢 The final result of the second integral is Pi, demonstrating that an improper integral with infinite bounds can converge to a finite value.
🤔 The video emphasizes the importance of understanding the behavior of functions at infinity, especially for natural logarithm and arctan functions.
📝 The process involves breaking down the integral into manageable parts, applying appropriate mathematical techniques, and evaluating limits.
👍 The video concludes by encouraging viewers to memorize important function graphs and to practice solving improper integrals.

Q & A

What are the three types of improper integrals mentioned in the video?
-The three types of improper integrals discussed are: 1) Discontinuity at either the lower bound 'a' or the upper bound 'b'. 2) Discontinuity somewhere in between 'a' and 'b'. 3) The bounds 'a' or 'b' being infinite, such as negative or positive infinity.
What is the fourth type of improper integral mentioned, which is a combination of the others?
-The fourth type is a combination of the first three, where there might be discontinuities at the bounds, within the interval, and at least one of the bounds is infinite.
What is the integral being evaluated in the first example of the video?
-The first integral evaluated is from 0 to Infinity of x^2 over (1 + x^3) dx.
Why is the integral of x^2 over (1 + x^3) from 0 to Infinity divergent?
-The integral diverges because as 'B' approaches Infinity, the natural logarithm of (1 + B^3) also goes to Infinity, resulting in a non-finite sum.
What substitution is used to evaluate the integral from 0 to Infinity of x^2 over (1 + x^3) dx?
-The substitution used is u = 1 + x^3, which leads to du = 3x^2 dx, and then the integral is simplified to 1/3 times the natural logarithm of the absolute value of u.
What is the integral being evaluated in the second example of the video?
-The second integral evaluated is from negative Infinity to Infinity of 1/(1 + x^2) dx.
How is the integral from negative Infinity to Infinity of 1/(1 + x^2) dx broken down?
-The integral is broken down into two parts by introducing a number 'C', and then using the property of integrals that the integral from 'a' to 'b' is the sum of the integrals from 'a' to 'C' and from 'C' to 'b'.
What is the result of the improper integral from negative Infinity to Infinity of 1/(1 + x^2) dx?
-The result of the improper integral is Pi, which is a finite value despite the integral having infinite bounds.
Why is the arctan function relevant to the second integral example in the video?
-The arctan function is relevant because 1/(1 + x^2) is the derivative of arctan(x), and the integral is evaluated by recognizing this relationship and applying limits as 'a' approaches negative Infinity and 'B' approaches positive Infinity.
What are the horizontal asymptotes of the arctan function that are important for understanding the limits in the second integral example?
-The horizontal asymptotes of the arctan function are at -π/2 as x approaches negative Infinity and π/2 as x approaches positive Infinity, which are crucial for evaluating the limits in the integral.
What is the significance of the graph of the arctan function in evaluating improper integrals and limits?
-The graph of the arctan function is significant because it helps in understanding the behavior of the function as it approaches Infinity and negative Infinity, which is essential for evaluating improper integrals and limits.

Outlines

00:00

📚 Introduction to Improper Integrals

The video script introduces the topic of improper integrals, distinguishing between three main types based on the presence of discontinuities at the bounds, within the bounds, or at infinite bounds. The script focuses on the third type, where at least one of the bounds is infinite. The first integral example given is from 0 to infinity of x^2 over (1 + x^3), which is approached by setting a limit as B approaches infinity and using a natural logarithm substitution to evaluate the integral, concluding that it diverges.

Mindmap

Keywords

💡Improper Integrals

Improper integrals are a type of definite integral where at least one of the limits of integration is infinite, or the integrand has a discontinuity within the interval of integration. In the video, the speaker discusses three types of improper integrals, including those with infinite bounds and those with discontinuities, which are the focus of the educational content.

💡Discontinuity

A discontinuity in a function occurs at a point where the function is not defined or the limit does not exist. In the context of improper integrals, the video mentions discontinuities at the bounds of the integral (A or B) or somewhere in between, which affects how the integral is evaluated.

💡Natural Logarithm

The natural logarithm, often denoted as ln(x), is the logarithm to the base e. It is used in calculus to solve integrals involving the reciprocal of a function, as shown in the video when integrating x^2 over (1 + x^3). The natural logarithm is a key concept in the first integral example provided.

💡Integration by Substitution

Integration by substitution is a method used to evaluate integrals by changing the variable of integration to simplify the integrand. In the script, the speaker uses this method by setting u as the denominator (1 + x^3) to integrate x^2 over (1 + x^3) dx, which is a fundamental technique in calculus.

💡Arctangent

The arctangent function, denoted as arctan(x) or tan^(-1)(x), is the inverse function of the tangent and is used to find the angle whose tangent is x. In the video, arctan is used to integrate 1 over (1 + x^2), which is a standard integral in calculus.

💡Horizontal Asymptote

A horizontal asymptote is a horizontal line that a function approaches as its input (x) goes to positive or negative infinity. The video discusses the horizontal asymptotes of the arctan function, which are at π/2 and -π/2, important for understanding the limits of improper integrals.

💡Convergence

In calculus, convergence refers to the property of a sequence or series to approach a certain value or behavior as its terms are increased indefinitely. The video explains that if the natural logarithm of infinity does not converge to a finite value, the integral diverges.

💡Diverges

A divergent integral is one that does not converge to a finite value. The video provides an example where the integral of x^2 over (1 + x^3) from 0 to infinity diverges because the natural logarithm of infinity does not yield a finite result.

💡Limits

In calculus, limits are used to define the value that a function or sequence approaches as the input approaches a certain point. The video uses limits to define the improper integrals with infinite bounds, such as the limit as B approaches infinity of the integral from 0 to B.

💡Pi

Pi (π) is a mathematical constant representing the ratio of a circle's circumference to its diameter. In the video, the final value of a particular improper integral from negative to positive infinity is shown to be π, which is a finite and well-known mathematical constant.

Highlights

Introduction to improper integrals and their types.

Discusses the first type of improper integrals with discontinuity at bounds A or B.

Explains the second type of improper integrals with discontinuity between A and B.

Introduces the third type of improper integrals with infinite bounds A or B.

Mentions the possibility of combining different types of improper integrals.

Begins with an example of an improper integral with infinite bounds from 0 to Infinity.

Integrates the function \( \frac{x^2}{1 + x^3} \) using substitution method with \( u = 1 + x^3 \).

Simplifies the integral to a natural logarithm function.

Applies the fundamental theorem of calculus to evaluate the integral.

Determines that the integral diverges as the natural logarithm of infinity is not finite.

Proceeds with another example of an improper integral from negative Infinity to Infinity.

Uses the property of integrals to split the integral into two parts.

Integrates the function \( \frac{1}{1 + x^2} \) using the arctan function.

Evaluates the limits as \( a \) approaches negative Infinity and \( b \) approaches Infinity.

Notes the importance of the arctan graph and its horizontal asymptotes.

Concludes that the improper integral converges to a finite value of Pi.

Encourages memorizing the arctan graph for its utility in solving similar problems.

Summarizes the process and outcomes of evaluating improper integrals with infinite bounds.

Transcripts

Browse More Related Video

Improper Integrals - Convergent or Divergent (Made Easy)

Improper Integrals BC Calc

Lesson 17 - Improper Integrals (Calculus 1 Tutor)

Improper Integrals - Convergence and Divergence - Calculus 2

Introduction to improper integrals | AP Calculus BC | Khan Academy

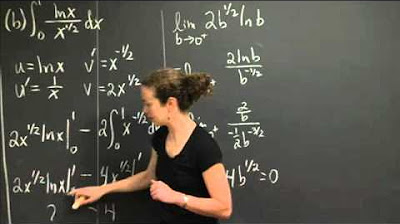
Improper Integrals | MIT 18.01SC Single Variable Calculus, Fall 2010

Improper Integrals - Infinite Bounds

Takeaways

Q & A

What are the three types of improper integrals mentioned in the video?

What is the fourth type of improper integral mentioned, which is a combination of the others?

What is the integral being evaluated in the first example of the video?

Why is the integral of x^2 over (1 + x^3) from 0 to Infinity divergent?

What substitution is used to evaluate the integral from 0 to Infinity of x^2 over (1 + x^3) dx?

What is the integral being evaluated in the second example of the video?

How is the integral from negative Infinity to Infinity of 1/(1 + x^2) dx broken down?

What is the result of the improper integral from negative Infinity to Infinity of 1/(1 + x^2) dx?

Why is the arctan function relevant to the second integral example in the video?

What are the horizontal asymptotes of the arctan function that are important for understanding the limits in the second integral example?

What is the significance of the graph of the arctan function in evaluating improper integrals and limits?