AP Calculus BC Lesson 6.13
TLDRThe video script delves into the concept of improper integrals, which are categorized by either infinite limits or infinite discontinuities within the integration interval. It explains how to evaluate these integrals using limits, providing examples of both convergent and divergent integrals. The script also discusses the use of integration techniques such as U-substitution and partial fractions for more complex improper integrals, and highlights the importance of identifying whether an integral converges to a finite value or diverges to infinity.
Takeaways
- 📚 Improper integrals are categorized into two types: those with infinite limits or infinite discontinuities within the interval.
- 🌐 Infinite limits involve calculating the area under a curve extending to infinity or negative infinity.
- 🚫 Infinite discontinuities occur when the integrand has a vertical asymptote within the interval, such as 1/x^2 from -1 to 1.
- 🔄 To evaluate improper integrals, replace the infinite limit with a variable (e.g., t) and use limits to find the area.
- 📈 The convergence of an improper integral is determined by the behavior of the integrand as the variable approaches infinity or negative infinity.
- 🔢 The integral converges if the power of x in the denominator is greater than 1, and diverges if it is less than or equal to 1.
- 🔄 For integrals with both limits infinite, split the integral into two parts and evaluate each separately to determine convergence or divergence.
- 📊 Proper techniques like U-substitution and partial fraction decomposition are often required to evaluate the integrals algebraically.
- 🌟 Even if an integral has an infinite bound, the area under the curve can still be finite, as demonstrated by the integral from 1 to infinity of 1/x^3 DX.
- 🚫 Divergent integrals do not have a finite value; they either approach positive or negative infinity or do not exist.
- 📝 When faced with an improper integral, always check for infinite discontinuities within the interval and apply the appropriate method to evaluate it.
Q & A
What is an improper integral?
-An improper integral is an integral that has either infinite limits or an infinite discontinuity in the interval for the integrand. It falls into two categories: one with infinite limits, such as from 1 to Infinity of e^x dx, and the other with an infinite discontinuity, like the integral from -1 to 1 of 1/x^2 dx, which has a vertical asymptote at x=0.
How can we evaluate an improper integral with infinite limits?
-To evaluate an improper integral with infinite limits, we replace the infinite limit with a variable and use a limit. For example, the integral from 1 to Infinity of 1/x^3 dx is evaluated by setting up the limit as T approaches Infinity of the integral from 1 to T of 1/x^3 dx, then solving the integral and finally substituting Infinity for T.
What is the difference between a convergent and a divergent integral?
-A convergent integral is one that approaches a finite value, meaning it has a numerical answer such as 1/2, 5, or -4. A divergent integral, on the other hand, does not approach a finite value; it either approaches positive or negative infinity or does not exist.
How can we determine if an improper integral with a power function in the denominator converges or diverges?
-An improper integral with a power function in the denominator, such as ∫ from a to Infinity of 1/x^p dx, converges if p > 1 and diverges if p ≤ 1.
What should we do if an improper integral has both lower and upper bounds as infinity?
-If an improper integral has both bounds as infinity and the function is continuous, we can split the integral into ∫ from negative Infinity to C of f(x) dx + ∫ from C to Infinity of f(x) dx, where C is any constant. We then evaluate each integral separately, and if either diverges, the whole integral diverges.
How does the presence of a vertical asymptote affect the evaluation of an improper integral?
-The presence of a vertical asymptote within the interval of integration can cause the improper integral to diverge. For instance, the integral from -1 to 1 of 1/x^2 dx cannot be evaluated directly because the function approaches infinity at x=0, leading to a divergent integral.
What is the area of the unbounded region between the graph of y = ln(x) + 5/x and the x-axis for x ≥ 20?
-The area of the unbounded region is infinite because the integral from 20 to Infinity of ln(x) + 5/x dx diverges, indicating that the area under the curve increases without bound as x approaches infinity.
For what values of w does the integral from 4 to Infinity of 1/(x^4w - 12) dx diverge?
-The integral diverges when 4w - 12 ≤ 1, which simplifies to w ≤ 13/4. Therefore, values of w that are less than or equal to 13/4 will make the integral diverge.
How can we find the value of the integral from 0 to 2 of 1/(x^2 - 2x + 1) dx?
-We first rewrite the function as 1/(x - 1)^2, then split the integral at the vertical asymptote x = 1. We evaluate the two separate improper integrals from 0 to 1 and from 1 to 2, using limits to handle the discontinuity at x = 1. If either of these integrals diverges, the entire integral diverges.
What is the value of the integral from 5 to Infinity of (3/(2x^2 - 7x + 5)) dx?
-The integral can be evaluated by using partial fraction decomposition to rewrite the given function as 2/(2x - 5) - 1/(x - 1). The integral is then the limit as T approaches Infinity of [ln|2x - 5| - ln|x - 1|] evaluated from 5 to T. Simplifying this expression gives us ln(8/5) as the value of the integral.
Outlines
📚 Introduction to Improper Integrals
This paragraph introduces the concept of improper integrals, which are categorized into two types: those with infinite limits and those with an infinite discontinuity within the integration interval. Examples of each type are provided, such as the integral from 1 to Infinity of e^x dx and the integral from -1 to 1 of 1/x^2 dx. The paragraph explains that improper integrals require a check for infinite discontinuities and that the evaluation of these integrals involves replacing the infinite limit with a variable and applying a limit to the integral.
🧮 Evaluating Improper Integrals with Infinite Limits
The paragraph delves into the algebraic evaluation of improper integrals with infinite limits. It illustrates the process using the example of the integral from 1 to Infinity of 1/x^3 dx. The method involves replacing the infinite limit with a variable (T), integrating the function, and then evaluating the limit as T approaches infinity. The example concludes with the integral converging to a finite value of one-half, demonstrating that not all improper integrals diverge to infinity.
🔢 Understanding Convergent and Divergent Integrals
This section discusses the criteria for determining whether an improper integral converges or diverges. It explains that integrals of the form ∫ from a to Infinity of 1/x^p dx will converge if p > 1 and diverge if p ≤ 1. The paragraph provides examples of both convergent and divergent integrals, highlighting the importance of this concept in evaluating improper integrals and the implications of obtaining finite numerical answers versus positive or negative infinity.
📈 Splitting Integrals with Infinite Upper and Lower Bounds
The paragraph addresses the evaluation of improper integrals where both the upper and lower bounds are infinite. It introduces a method for handling such integrals by splitting them into two integrals with finite bounds. The process involves evaluating each new integral separately and concluding that if either integral diverges, the entire integral diverges. An example is provided, demonstrating the method and its application.
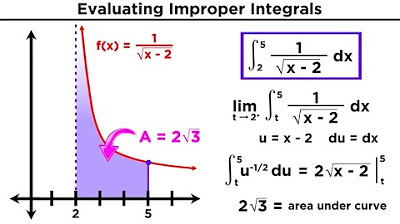
🤔 Dealing with Improper Integrals at a Point of Discontinuity
This section focuses on improper integrals that have a vertical asymptote within the interval of integration. The method of splitting the integral at the point of discontinuity is discussed, with an example illustrating the process. The paragraph emphasizes that if either of the resulting integrals diverges, the entire integral is considered divergent.
🌐 Complex Integration Techniques for Improper Integrals
The paragraph discusses the use of more complex integration techniques, such as U-substitution, partial fractions, or integration by parts, to evaluate certain types of improper integrals. An example involving U-substitution is worked out in detail, showing how to simplify the integrand and evaluate the integral with an infinite limit.
📊 Evaluating an Improper Integral with a Natural Log Function
This section presents an example of evaluating an improper integral involving a natural log function with an infinite upper bound. The method of U-substitution is used, and the paragraph concludes with the integral converging to a specific value, demonstrating the application of the fundamental theorem of calculus and the importance of recognizing when an integral diverges or converges to a finite number.
🏞 Calculating the Area of an Unbounded Region
The paragraph discusses the calculation of the area of an unbounded region between a curve and the x-axis from a certain point to infinity. It explains the process of evaluating an improper integral with an infinite upper bound by replacing it with a limit and then integrating the function. The example provided concludes with the area of the region being infinite, indicating that the integral is divergent.
🔍 Determining Divergence for a Specific Integral
This section examines a specific integral and the values of a parameter for which the integral diverges. It applies the rule that an integral of the form 1/x^p diverges if p ≤ 1. The paragraph calculates the value of the parameter that makes the integral diverge and provides the correct answer based on this criterion.
🧬 Evaluating an Improper Integral with a Factorable Denominator
The paragraph presents a method for evaluating an improper integral with a factorable denominator that contains a vertical asymptote. The integral is split into two parts at the point of discontinuity, and the limits are evaluated separately. The paragraph concludes by showing that one part of the integral does not exist, implying that the entire integral diverges.
📐 Applying Partial Fractions to Evaluate an Integral
This section describes the process of using partial fractions to evaluate an improper integral with an infinite upper bound. The method involves breaking down the integrand into simpler parts, applying U-substitution to one part, and simplifying the other part directly. The paragraph concludes with the integral being equal to the natural log of a specific fraction, demonstrating the successful application of the technique.
Mindmap
Keywords
💡Improper Integrals
💡Infinite Limits
💡Infinite Discontinuity
💡Convergent Integrals
💡Divergent Integrals
💡Limits
💡Vertical Asymptote
💡Fundamental Theorem of Calculus
💡Antiderivatives
💡Power Rule
Highlights
Improper integrals are defined as integrals with infinite limits or infinite discontinuities in the interval.
An integral with infinite limits could look like ∫ from 1 to Infinity of e^x dx.
An integral with an infinite discontinuity in the interval could be ∫ from -1 to 1 of 1/x^2 dx due to the vertical asymptote at x=0.
To evaluate improper integrals algebraically, replace the infinite limit with a variable and use a limit.
The integral ∫ from 1 to Infinity of 1/x^3 dx converges to 1/2.
The integral ∫ from 1 to Infinity of 1/√x dx diverges to positive infinity.
Improper integrals with lower and upper bounds of infinity can be split into two integrals from constants to infinity for easier evaluation.
The integral ∫ from -∞ to ∞ of 3x^2 dx diverges as it approaches positive infinity.
Integrals with a vertical asymptote at a point within the interval can be split at that point for evaluation.
U-substitution is a useful technique for evaluating improper integrals with complex integrands.
The integral ∫ from 1 to Infinity of x^3/(1+2x^4)^2 dx converges to 1/24.
The area of an unbounded region can be found by evaluating an improper integral from a lower bound to infinity.
The integral ∫ from 20 to Infinity of (ln(x) + 5)/x^5 dx diverges.
The integral ∫ from 4 to Infinity of 1/(x^4w - 12) dx diverges for w values less than or equal to 13/4.
The integral ∫ from 0 to 2 of 1/(x^2 - 2x + 1) dx diverges because of a vertical asymptote at x=1.
The integral ∫ from 5 to Infinity of (3/(2x^2 - 7x + 5)) dx can be evaluated using partial fraction decomposition.
The integral ∫ from 5 to Infinity of f(x) dx equals the natural log of eight-fifths.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: