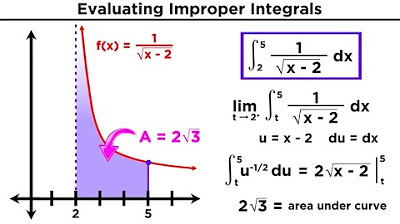
Improper Integrals BC Calc

Chad Gilliland
24 Jan 201311:06
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the concept of improper integrals, which are integrals with limits extending to infinity or containing discontinuities. The instructor explains how to approach these integrals by setting finite limits and then taking the limit as it approaches infinity or zero, depending on the discontinuity's location. Examples are provided, including the integral of 1/x^2 from 1 to infinity, which converges to 1, and the integral of 1/x^2 from -1 to 0, which diverges. The importance of identifying and handling discontinuities within the integral's range is emphasized, with strategies for evaluating such integrals demonstrated through practical examples.

Takeaways
  • 📚 The topic discussed is improper integrals, which involve limits that extend to infinity or have discontinuities within the integration interval.
  • 📉 The first example given is the integral of 1/x^2 from 1 to infinity, which is approached by considering the limit as B approaches infinity of the integral from 1 to B.
  • 🔍 An antiderivative for 1/x^2 is -1/x, and the process involves evaluating this antiderivative between the limits and then taking the limit as B approaches infinity.
  • 📈 The result of the first integral converges to 1, indicating a finite area under the curve as x approaches infinity.
  • 🤔 The second example involves an integral with a discontinuity at x=0, specifically the integral of 1/x^2 from -1 to 0, which requires a limit as B approaches 0 from the left.
  • 💥 The second integral diverges, meaning the area under the curve grows to infinity as x approaches 0 from the left.
  • 📐 The third example shows an integral with a discontinuity in the middle of the interval, such as the integral of 1/x^3 from -1 to 2, which requires splitting the integral at the point of discontinuity.
  • 📝 The process involves checking for infinite discontinuities both at the endpoints and in the interior of the interval for integrals.
  • 👨‍🏫 The instructor emphasizes the need for practice, indicating that understanding improper integrals can be complex and requires focused attention.
  • 🛑 The script includes an apology for a pause, suggesting that the recording may have been interrupted or the instructor may have experienced a momentary difficulty.
  • 🔢 The use of a calculator is mentioned, particularly for integrals that extend to infinity, where the calculator can provide a numerical answer.
Q & A

  • What is an improper integral?

    -An improper integral is an integral that has an infinite limit of integration, or an integrand with a discontinuity within the interval of integration. It requires a limit process to evaluate.

  • Why can't we integrate with a discontinuity?

    -We can't integrate with a discontinuity because the fundamental theorem of calculus doesn't apply to functions that are not continuous over the interval of integration.

  • What is the antiderivative of 1 over x squared?

    -The antiderivative of 1 over x squared is negative 1 over x.

  • How do we handle an improper integral that goes to infinity?

    -We handle an improper integral that goes to infinity by setting a finite limit, integrating from the lower bound to this limit, and then taking the limit as this limit approaches infinity.

  • What does it mean for an integral to converge?

    -An integral converges if it results in a finite value after the limit process is applied, indicating that the area under the curve is finite.

  • What is the result of the improper integral from 1 to infinity of 1 over x squared?

    -The result of the improper integral from 1 to infinity of 1 over x squared is 1, indicating that the area under the curve converges to 1.

  • What is the issue with integrating 1 over x squared from negative 1 to 0?

    -The issue is that the function has a vertical asymptote at 0, which means it is undefined at that point, making the integral improper.

  • How do we evaluate the improper integral from negative 1 to 0 of 1 over x squared?

    -We evaluate it by taking the limit as B approaches 0 from the left, integrating from negative 1 to B of 1 over x squared, and then applying the limit process.

  • What is the result of the improper integral from negative 1 to 0 of 1 over x squared?

    -The result is that the integral diverges to infinity, as the area under the curve grows without bound approaching the discontinuity at 0.

  • What should we do if there is a discontinuity in the interior of the integration interval?

    -We should split the integral at the point of discontinuity, creating two separate integrals that avoid the discontinuity, and then evaluate each separately.

  • How do we handle an integral with a discontinuity at the endpoint?

    -We handle it by approaching the endpoint with a limit, integrating from the starting point to a variable that approaches the endpoint, and then applying the limit process.

  • What does the term 'divergent integral' mean?

    -A divergent integral refers to an improper integral that does not converge to a finite value, often because the area under the curve grows to infinity.

Outlines
00:00
📚 Introduction to Improper Integrals

This paragraph introduces the concept of improper integrals, which are integrals that involve limits to infinity or have discontinuities within the interval of integration. The instructor uses the example of the integral of 1 over x squared from 1 to infinity to explain the process of evaluating such integrals. The key point is that instead of directly integrating over an infinite interval, a finite limit is used, and then the limit is taken as this value approaches infinity. The antiderivative of 1 over x squared is found to be negative 1 over x, and the limit process is applied to determine the area under the curve, which converges to 1. This approach is essential for dealing with integrals that have infinite limits or discontinuities.

05:03
🔍 Dealing with Discontinuities at Endpoints

The second paragraph delves into the complexities of improper integrals that have discontinuities at the endpoints of the integration interval. The example given is the integral of 1 over x squared from negative 1 to 0, which includes a vertical asymptote at x equals 0, making the function undefined at that point. To address this, the integral is split into two parts, with the limit taken as B approaches 0 from the left for the first part and from the right for the second part. The process involves evaluating the antiderivative of the function and applying the limit to find the area under the curve. In this case, the integral from negative 1 to 0 diverges to infinity, indicating an infinite area, which is not possible to calculate.

10:06
📐 Handling Discontinuities in the Interior

The final paragraph discusses the scenario where the discontinuity lies within the interior of the integration interval. The integral of 1 over x cubed from negative 1 to 2 is used as an example, where the function has a vertical asymptote at x equals 0. To handle this, the integral is split across the discontinuity, with two separate integrals calculated: one from negative 1 to 0 and the other from 0 to 2. The limits are taken as B approaches 0 from the left for the first integral and from the right for the second integral. This approach is necessary to evaluate the integrals correctly and understand the behavior of the function at points of discontinuity within the interval.

Mindmap
Keywords
💡Improper Integrals
Improper integrals are a type of integral that either has an infinite limit of integration or includes a discontinuity within the interval of integration. In the video, the concept is central to understanding how to evaluate areas under curves that extend to infinity or have points of discontinuity, such as vertical asymptotes. Examples given include the integral from 1 to infinity of 1 over x squared and from negative 1 to 0 of 1 over x squared, illustrating the process of handling these improper integrals.
💡Infinity
In the context of the video, infinity refers to the unbounded extent of the integral's limits, specifically when the integral extends to positive or negative infinity. It is a key concept in improper integrals, as it challenges the traditional finite limits of integration. The script discusses how to handle integrals that go 'all the way out to infinity,' using limits to evaluate their convergence or divergence.
💡Discontinuity
Discontinuity in the video refers to a point within the integral's interval where the function is not defined, typically a vertical asymptote. The script explains that integrals cannot be directly evaluated across discontinuities and demonstrates how to work around this by splitting the integral or approaching the discontinuity with limits.
💡Antiderivative
An antiderivative is a function that represents the reverse process of differentiation. In the context of the video, finding the antiderivative of a function is a necessary step in evaluating improper integrals. The script shows the process of finding antiderivatives for functions like 1 over x squared and 1 over x cubed to set up the integrals for evaluation.
💡Convergence
Convergence in the video pertains to the property of an improper integral where the area under the curve approaches a finite value. The script uses the term to describe when an integral has a finite result, such as the integral from 1 to infinity of 1 over x squared, which converges to 1.
💡Divergence
Divergence is the opposite of convergence and is used in the video to describe when an improper integral grows without bound, leading to an infinite area. The script illustrates divergence with the integral from negative 1 to 0 of 1 over x squared, which approaches infinity as it includes the discontinuity at x equals 0.
💡Vertical Asymptote
A vertical asymptote is a vertical line that the graph of a function approaches but never crosses, typically occurring where the function is undefined. In the video, vertical asymptotes are points of discontinuity that affect the evaluation of improper integrals, such as at x equals 0 in the integrals of 1 over x squared and 1 over x cubed.
💡Limit
In the context of improper integrals, a limit is used to approach a point of discontinuity or infinity. The video script explains how to use limits to evaluate integrals that would otherwise be undefined, by approaching the problematic points from the left or right, or by extending the limits to infinity.
💡Integration
Integration is the mathematical process of finding the integral of a function, which represents the area under the curve of that function. The video focuses on the process of integration in the context of improper integrals, where traditional methods must be adapted to handle infinite limits or discontinuities.
💡Area Under the Curve
The area under the curve is a geometric interpretation of an integral, representing the space enclosed by the curve, the x-axis, and the limits of integration. The video script discusses finding this area for functions with improper integrals, such as those extending to infinity or having discontinuities.
Highlights

Introduction to improper integrals and their types.

Explaining the concept of improper integrals due to infinite limits.

Discussing improper integrals with discontinuities inside the integration interval.

Starting with a simple example of the integral of 1/x^2 from 1 to infinity.

Using a finite value B to trick the interval for integration.

Combining limits and integration to evaluate improper integrals.

Finding the antiderivative of 1/x^2 and evaluating it between 1 and B.

Evaluating the limit as B approaches infinity to find the area under the curve.

The integral from 1 to infinity of 1/x^2 converges to 1.

Demonstrating the use of a calculator to evaluate the integral from 1 to infinity.

Exploring the integral from negative 1 to 0 of 1/x^2 and its challenges.

Handling discontinuities at endpoints by approaching zero from the left.

Evaluating the limit as B approaches zero from the left for the integral.

Determining that the integral from negative 1 to 0 of 1/x^2 diverges.

Introducing the concept of discontinuities in the interior of the integration interval.

Splitting the integral across discontinuities to handle interior points.

Encouraging practice and focus for understanding improper integrals.

Transcripts

Browse More Related Video

Improper Integrals - Convergence and Divergence - Calculus 2

Evaluating Improper Integrals

Introduction to improper integrals | AP Calculus BC | Khan Academy

Improper Integrals - Convergent or Divergent (Made Easy)

AP Calculus BC Lesson 6.13

Improper Integrals - Infinite Bounds

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Improper IntegralsInfinite LimitsDiscontinuityMathematicsCalculusAntiderivativeArea Under CurveVertical AsymptoteIntegral EvaluationEducational Content