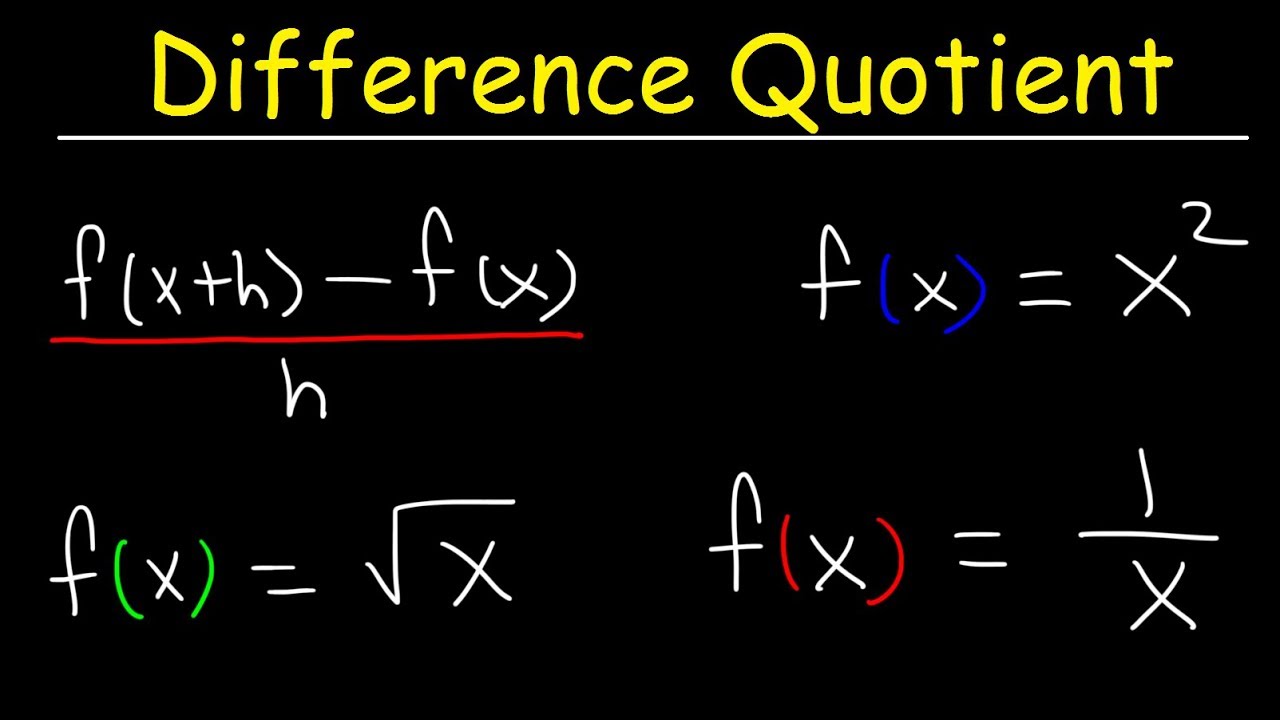Definition of the Derivative

The Organic Chemistry Tutor

22 Feb 201823:31

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers a comprehensive guide on calculating derivatives using the definition of the derivative and its limit process. It explains how to find the first derivative of various functions, such as linear functions, quadratic functions, radical functions, and polynomial functions, by applying the formula f'(x) = lim(h->0) [(f(x+h) - f(x))/h]. The examples provided, including 5x - 4, x^2, 1/x, and the square root of x, demonstrate the step-by-step process of simplifying expressions and evaluating limits to arrive at the derivative. The script effectively supports viewers in understanding the concept and application of derivatives in calculus.

Takeaways

📚 The derivative of a function can be found using the definition of the derivative, which involves the limit process.
🔢 The notation f'(x) represents the derivative of the function f(x).
🎓 The basic formula for the derivative is: f'(x) = lim (h->0) [(f(x+h) - f(x))/h].
📈 For a linear function, such as f(x) = 5x - 4, the derivative is the coefficient of x, resulting in f'(x) = 5.
🏠 When finding the derivative of x^2, the result is f'(x) = 2x, using the limit process and expansion of the expression.
🔄 For functions like 1/x, the derivative is found by applying the limit and simplifying the complex fraction, resulting in f'(x) = -1/x^2.
🌐 For radical functions, such as the square root of x (√x), the derivative requires the use of conjugates and simplification, yielding f'(x) = 1/(2√x).
📊 When dealing with polynomial functions, the derivative is calculated by applying the limit process to each term with its respective power of x, leading to f'(x) = 2x - 5 for f(x) = x^2 - 5x + 9.
📝 The process of finding derivatives involves replacing x with (x+h), expanding expressions, simplifying, and evaluating limits.
🎓 Understanding the rules for handling complex fractions, radicals, and polynomials is crucial for calculating derivatives.
📈 Derivatives provide insight into the rate of change or slope of a function at any given point.

Q & A

What is the definition of the derivative?
-The derivative of a function, denoted as f'(x), is defined as the limit, as h approaches zero, of the difference quotient [f(x + h) - f(x)] divided by h.
How do you find the derivative of a linear function?
-For a linear function, such as f(x) = 5x - 4, the derivative can be found by identifying the slope of the line, which is the coefficient of x. In this case, the derivative f'(x) is 5, as it represents the constant rate of change of the function.
What is the first derivative of the function f(x) = x^2?
-Using the definition of the derivative, the first derivative of f(x) = x^2 is found to be f'(x) = 2x. This result comes from applying the limit process and simplifying the expression.
How do you handle a complex fraction when finding derivatives?
-When dealing with complex fractions, you should multiply both the numerator and the denominator by the common denominator to simplify the expression. This process eliminates the fractions and allows you to continue applying the limit process to find the derivative.
What is the derivative of the function f(x) = 1/x?
-The derivative of f(x) = 1/x, using the limit definition, is found to be f'(x) = -1/x^2. This is derived by applying the limit process to the complex fraction and simplifying the result.
How do you find the derivative of a radical in the denominator, like 8/√x?
-To find the derivative of a function with a radical in the denominator, such as 8/√x, you first multiply the numerator and the denominator by the conjugate of the denominator to eliminate the radical in the numerator. After simplifying and applying the limit process, the derivative is found to be -4/x√x.
What is the first derivative of the polynomial function f(x) = x^2 - 5x + 9?
-The first derivative of the polynomial function f(x) = x^2 - 5x + 9 is f'(x) = 2x - 5. This is obtained by applying the power rule to each term and simplifying the result.
What is the power rule for derivatives?
-The power rule states that the derivative of x^n, where n is a constant, is nx^(n-1). This rule is used to find the derivatives of monomials and can be extended to work with polynomials by applying it to each term separately.
How do you simplify the expression when the limit involves a radical in both the numerator and the denominator?
-To simplify such an expression, you first multiply both the numerator and the denominator by the conjugate of the numerator to eliminate the radical. After simplifying, you can cancel out common terms and apply the limit process to find the derivative.
What is the role of the limit process in finding derivatives?
-The limit process is fundamental in finding derivatives as it captures the instantaneous rate of change of a function at a particular point. By taking the limit as h approaches zero, we obtain the derivative, which represents the slope of the tangent line to the function at that point.
What is the significance of the derivative in understanding a function's behavior?
-The derivative of a function provides valuable information about the function's behavior, such as its rate of change, the slope of its tangent lines, and points of inflection. It is a crucial tool in calculus for analyzing the properties of functions and their graphs.

Outlines

00:00

📚 Introduction to Derivatives

This paragraph introduces the concept of derivatives and explains how to find the derivative of a function using the definition of the derivative formula. It emphasizes the limit process and how f'(x) represents the derivative of f(x). The paragraph uses the example of a linear function, 5x - 4, to demonstrate the process of finding the first derivative by applying the formula and simplifying the expression. The result of the derivative for this example is 5, highlighting the importance of understanding the limit process in calculus.

05:03

📈 Derivative of Quadratic Functions

The paragraph delves into the process of finding the first derivative of quadratic functions, using the example of f(x) = x^2. It explains the application of the derivative definition formula and the steps to simplify the resulting expression. The paragraph details the expansion of the expression, combining like terms, and factoring out an h to isolate the derivative. The final derivative for the given example is 2x, reinforcing the concept that the derivative of a quadratic function is linear.

10:03

🔄 Handling Complex Fractions

This paragraph addresses the challenge of dealing with complex fractions when finding derivatives. It uses the function f(x) = 1/x to illustrate how to handle such cases. The explanation includes multiplying the numerator and denominator by a common denominator to eliminate the fraction and then applying the limit process. The paragraph concludes with the derivative of 1/x being -1/x^2, demonstrating the method for handling complex fractions in calculus.

15:04

🌟 Derivatives with Radicals

The paragraph focuses on finding derivatives when the function involves radicals, such as f(x) = √x. It outlines the steps to simplify the expression by multiplying the numerator and denominator by the conjugate of the numerator. The paragraph explains the process of canceling terms and applying direct substitution to find the limit as h approaches zero. The final derivative for the square root function is 1/(2√x), showcasing the approach to handling radicals in calculus.

20:04

📊 Polynomial Derivatives

The final paragraph discusses the process of finding the first derivative of a polynomial function, exemplified by f(x) = x^2 - 5x + 9. It details the steps of expanding the function, distributing terms, and simplifying the expression to find the derivative. The paragraph emphasizes factoring out the greatest common factor and using direct substitution to arrive at the derivative, 2x - 5. This example solidifies the understanding of polynomial derivatives and their calculation in calculus.

Mindmap

Keywords

💡Derivative

The derivative is a fundamental concept in calculus that represents the rate of change of a function at a given point. It is used to analyze the behavior of functions, such as their slopes, critical points, and inflection points. In the video, the derivative is calculated using the definition of the derivative, which involves taking the limit as 'h' approaches zero of the difference quotient of the function.

💡Limit

In mathematics, a limit is a value that a function or sequence approaches as the input (or index) approaches some value. Limits are essential in understanding the behavior of functions, especially when inputs are very large or very close to a particular point. In the context of the video, limits are used to define and calculate derivatives, where the limit is taken as 'h' approaches zero.

💡Function

A function is a mathematical relation between a set of inputs and a set of permissible outputs. Each input is related to exactly one output. Functions are central to many areas of mathematics and its applications, including calculus. In the video, various functions are analyzed to find their derivatives.

💡Linear Function

A linear function is a function of the form f(x) = mx + b, where m and b are constants, and m is the slope of the line. Linear functions represent straight lines when graphed and have a constant rate of change. The derivative of a linear function is the slope of the line, which is a constant value.

💡Quadratic Function

A quadratic function is a function of the form f(x) = ax^2 + bx + c, where a, b, and c are constants, and the highest power of x is 2. Quadratic functions represent parabolic shapes when graphed and have a variable rate of change. The derivative of a quadratic function is a linear function that gives the rate of change at any point on the parabola.

💡Rational Function

A rational function is a function of the form f(x) = P(x)/Q(x), where P(x) and Q(x) are polynomials and Q(x) ≠ 0. Rational functions can represent a variety of shapes, including lines, parabolas, and hyperbolas, and have varying rates of change. The derivative of a rational function is found by applying the limit definition and may involve complex algebraic manipulation.

💡Slope

Slope is a measure of the steepness of a line, representing the rate of change between the y-values and x-values on a graph. In calculus, the slope of a curve at a particular point is given by the derivative of the function at that point. The slope can be positive, negative, or zero, indicating the direction and rate of change of the function.

💡Difference Quotient

The difference quotient is a formula used in calculus to find the average rate of change of a function over an interval. It is the foundation for the definition of the derivative and is calculated as [f(x+h) - f(x)] / h, where 'h' is a small increment in the x-value. As 'h' approaches zero, the difference quotient approaches the derivative at x.

💡Complex Fraction

A complex fraction is a fraction that has another fraction as its numerator or denominator. To simplify complex fractions, they are often multiplied by the least common denominator (LCD) to eliminate the fractions within the fractions. This process is also used in calculus when finding derivatives of functions with radical expressions in the denominator.

💡Direct Substitution

Direct substitution is a method used in calculus where the value of a variable is directly replaced with another value in an expression to simplify or evaluate it. This technique is particularly useful when evaluating limits, as it involves substituting the value that the variable approaches in the limit expression.

💡Conjugate

In mathematics, a conjugate is a term that is used in the context of rational expressions and radicals. For a given binomial expression, the conjugate is the expression obtained by changing the sign of the term with a negative coefficient. Conjugates are used to simplify radical expressions by multiplying the numerator and denominator, which helps in rationalizing the denominator.

Highlights

Introduction to the concept of derivatives and their calculation using the definition of the derivative.

Derivative represented as f prime of x, denoting the derivative of f of x.

Explanation of the limit process involved in finding the derivative of a function.

Derivative calculation for a linear function, f(x) = 5x - 4.

Derivative result for the linear function is a constant 5.

Derivative calculation for the quadratic function, f(x) = x^2.

Derivative of x^2 is 2x, using the definition of the derivative.

Derivative calculation for the function f(x) = 1/x.

Derivative of 1/x is -1/x^2, using limit process and simplifying complex fractions.

Derivative calculation for the radical function, f(x) = √x.

Derivative of √x is 1/(2√x), using the limit process and conjugate for radicals.

Derivative calculation for a function with a radical in the denominator, f(x) = 8/√x.

Derivative of 8/√x is -4/x√x, by eliminating fractions and using the limit process.

Derivative calculation for a polynomial function, f(x) = x^2 - 5x + 9.

Derivative of x^2 - 5x + 9 is 2x - 5, using the limit process and polynomial expansion.

Explanation of how to handle complex fractions and radicals in derivative calculations.

Demonstration of factoring out the greatest common factor in the numerator to simplify the limit expression.

Use of direct substitution to find the derivative when approaching h to zero.

Transcripts

Browse More Related Video

Finding Derivative Using Limit Definition

Difference Quotient

Applying the Definition of the Derivative to 1/x

Derivatives of inverse functions: from equation | AP Calculus AB | Khan Academy

First principles grade 12: Practice

AP Calculus AB: Lesson 2.2 The Derivative Function

Related Tags

Calculus Derivatives Limits Linear Functions Quadratic Functions Polynomial Functions Math Education Online Learning Mathematics Tutorial Video Content