AP Physics 1 - Torque
TLDRIn this informative video, Dan Fullerton discusses the concept of torque, a force that causes an object to rotate. He explains torque as a vector, symbolized by the Greek letter tau, and its dependence on the force applied, the lever arm, and the angle of application. The video covers the principles of equilibrium, including static, dynamic, and rotational equilibrium, and provides examples of calculating torque and analyzing systems in balance. The content is engaging and educational, offering a clear understanding of rotational physics and its practical applications.
Takeaways
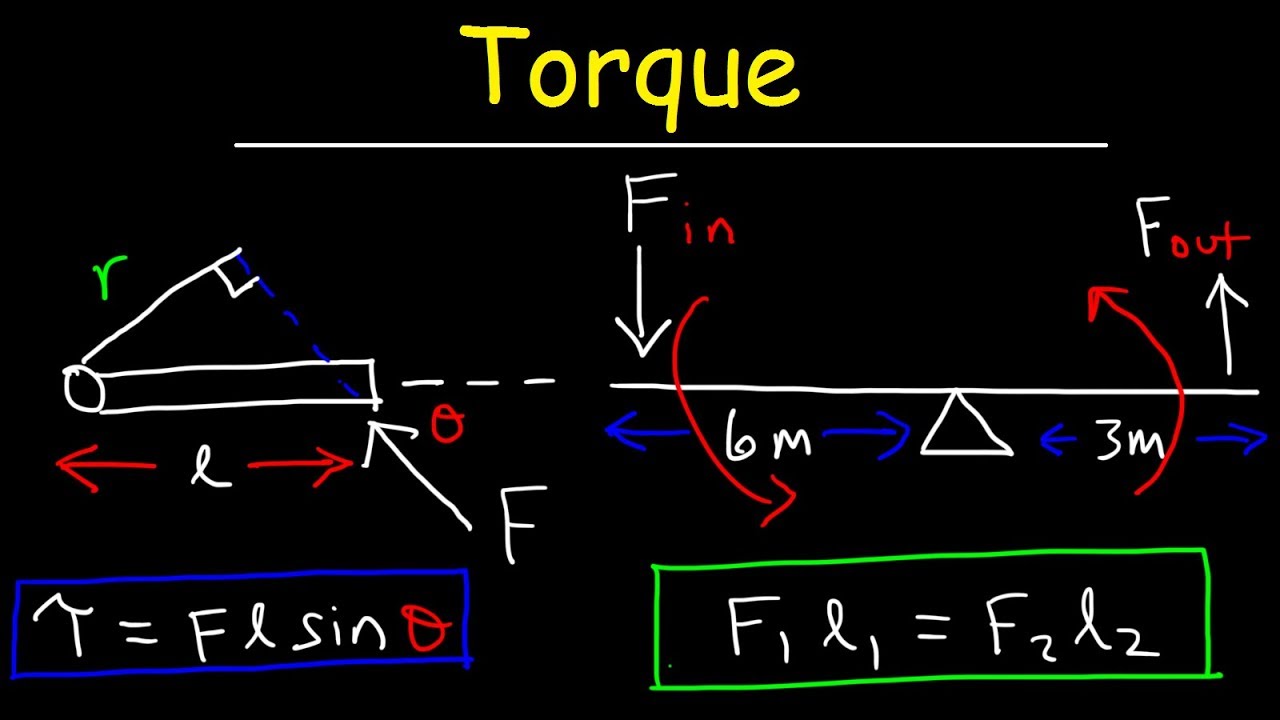
- 📌 Torque (τ) is a vector quantity that causes an object to rotate, represented by the Greek letter tau.
- 🔄 For a force to create torque, it must be perpendicular to the displacement, resulting in rotation.
- 📏 The leverage (R), or the distance from the point of rotation to where the force is applied, increases the torque.
- 🔧 The magnitude of torque is calculated as the product of the force (F), the lever arm (R), and the sine of the angle (θ) between them: τ = F * R * sin(θ).
- 👌 The direction of the torque vector is found using the right-hand rule, which points the thumb in the direction of the torque when fingers are in the direction of R and bent towards F.
- 🔄 Positive torques result in counterclockwise rotation, while negative torques cause clockwise rotation.
- ⚖️ Translational and rotational variables have analogs: net force is to net torque as mass is to moment of inertia (I), acceleration is to angular acceleration, and so on.
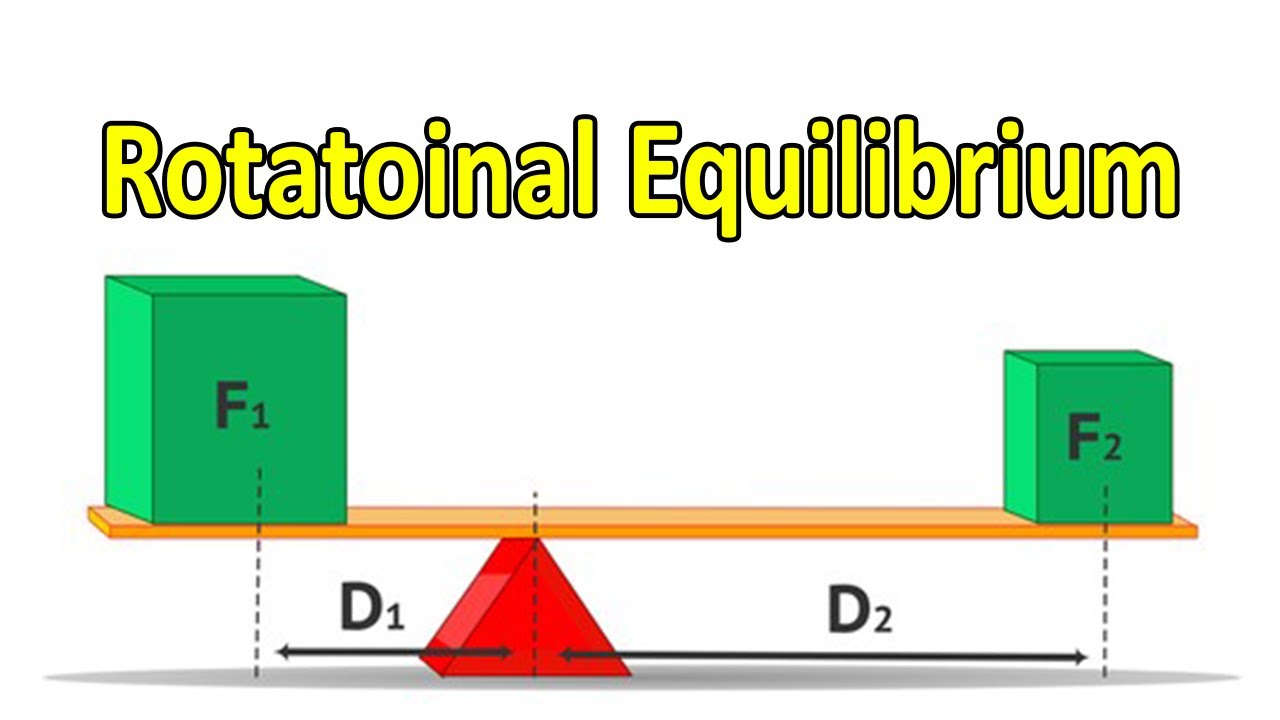
- 🌐 Equilibrium types include static (no motion), dynamic (constant velocity), and rotational (constant angular velocity).
- 🔩 When calculating torque with given force and angle, the length of the lever arm can be determined by rearranging the torque equation.
- 🔢 In a system with multiple forces and torques, the sum of torques can be used to find unknown forces or distances when equilibrium conditions are met.
- ⚖️ The position of masses on a lever (like a teeter-totter) can be determined by setting up equilibrium equations based on net torque being zero.
Q & A
What is the definition of torque?
-Torque is a vector quantity, represented by the Greek letter tau, that describes the force causing an object to rotate. It is perpendicular to the displacement, resulting in rotation.
What is the significance of the lever arm in the context of torque?
-The lever arm, or R, is the distance from the point of rotation to where the force is applied. It determines the effectiveness of the force in creating torque; the longer the lever arm, the more torque is generated for a given force.
How is the magnitude of the torque vector calculated?
-The magnitude of the torque vector is calculated using the formula tau (τ) = F * R * sin(θ), where F is the force applied, R is the lever arm, and θ is the angle between the force vector and the lever arm.
What is the right-hand rule, and how is it used to determine the direction of the torque vector?
-The right-hand rule is a convention used to determine the direction of the torque vector. By pointing the fingers of the right hand in the direction of the lever arm and curling them towards the direction of the force vector, the thumb points in the direction of the torque vector.
What are the differences between positive and negative torque?
-Positive torque causes counterclockwise rotation, while negative torque causes clockwise rotation. The sign of the torque depends on the direction of the applied force relative to the lever arm.
What are the three types of equilibrium discussed in the script?
-The three types of equilibrium are static equilibrium, where the net force and net torque are zero and the system is at rest; dynamic equilibrium, where the net force and net torque are zero and the system moves at constant translational and rotational velocity; and rotational equilibrium, where the net torque on an object is zero, allowing it to maintain its current state of angular velocity.
How is the moment of inertia related to mass in rotational physics?
-The moment of inertia is the rotational analog of mass. It represents how difficult it is to spin an object about an axis and is used in the equation for net torque, which is equal to the moment of inertia times angular acceleration (τ = I * α).
What is the relationship between linear and rotational variables?
-Linear and rotational variables are analogous, with net force being equivalent to net torque, mass to moment of inertia, acceleration vector to angular acceleration, displacement (ΔX) to angular displacement (ΔΘ), and velocity to angular velocity.
In the example of the pirate captain turning the ship's wheel, how much torque is applied?
-The pirate captain applies a torque of approximately 3.94 Newton-meters when using a force of 20 Newtons at a radius of 0.2 meters with an angle of 80 degrees to the line of action.
How can you find the force applied by a wrench based on the torque and the length of the wrench?
-The force (F) applied by the wrench can be found using the formula F = torque / (R * sin(θ)). If the torque is 100 Newton-meters, the wrench is 0.4 meters long, and the angle is 90 degrees (sin(90°) = 1), the force applied is 250 Newtons.
What is the tension in the wire needed to prevent the sign from rotating in the 'signpost problem'?
-The tension in the wire required to prevent the 3 kg sign from rotating is 55 Newtons, calculated by considering the net torque to be zero and solving for the tension (T) based on the forces and lever arms acting on the pole.
Where must Katrina sit on the teeter-totter to maintain static equilibrium with Marisa, and what is the force on the fulcrum?
-Katrina must sit 0.6 meters from the fulcrum to maintain static equilibrium with Marisa, who sits 1 meter from the fulcrum. The force on the fulcrum is 1200 Newtons, calculated by considering the combined weight of Marisa and Katrina and the balance of torques.
Outlines
📚 Introduction to Torque and Equilibrium
This paragraph introduces the concept of torque, which is a force that causes an object to rotate, and its representation using the Greek letter tau. It explains that torque is perpendicular to displacement, causing rotation, and its magnitude depends on the force, the lever arm (distance from the point of rotation), and the sine of the angle between the force and the lever arm. The right-hand rule is introduced to determine the direction of the torque vector. The paragraph also discusses rotational analogs of linear physics concepts, such as force and mass being analogous to torque and moment of inertia, respectively. Equilibrium is defined in three forms: static, dynamic, and rotational, each with its conditions. A practical example of a pirate captain applying force to a ship's wheel is used to calculate the torque applied.
🔧 Calculating Torque and Mechanical Advantage
This paragraph delves into the calculation of torque and force in different scenarios. It begins with a mechanic applying a torque of 100 Newton meters and calculates the force applied given the length of the wrench. The concept of lever arm and its impact on the required force is discussed. The paragraph then presents a problem involving a sign hanging from a pole, calculating the tension in the wire preventing the sign from rotating. The solution involves analyzing the forces and torques acting on the system and applying the principle of equilibrium to find the tension. Lastly, it discusses a seesaw problem, where the positions of two individuals are determined to maintain static equilibrium, and the force on the fulcrum is calculated using Newton's second law.
🎓 Conclusion and Further Learning
In the concluding paragraph, the video script wraps up the discussion on torque and equilibrium. It emphasizes the importance of understanding these concepts in physics and problem-solving. The host encourages viewers to continue learning and seeking more information, directing them to a website for additional resources. The paragraph ends on a positive note, wishing viewers a great day and highlighting the goal of providing a solid foundation for further exploration of physics topics.
Mindmap
Keywords
💡Torque
💡Rigid Object
💡Equilibrium
💡Lever Arm
💡Right-Hand Rule
💡Moment of Inertia
💡Angular Acceleration
💡Translational and Rotational Analogs
💡Static Equilibrium
💡Dynamic Equilibrium
💡Rotational Equilibrium
Highlights
Torque is a vector represented by the Greek letter tau.
Torque is a force that causes an object to turn, and it must be perpendicular to the displacement.
The lever arm (R) is the distance from the point of rotation to where the force is applied.
The magnitude of the torque vector is calculated as (F * R * sin(theta))
The direction of the torque vector is perpendicular to both the position vector and the force vector.
The right-hand rule is used to determine the direction of the torque vector.
Positive torques cause counterclockwise rotation, and negative torques cause clockwise rotation.
In the rotational world, net force is analogous to net torque, mass to moment of inertia, acceleration to angular acceleration, displacement to angular displacement, and velocity to angular velocity.
Static equilibrium implies that the net force and net torque are zero and the system is at rest.
Dynamic equilibrium implies that the net force and net torque are zero and the system is moving at constant translational and rotational velocity.
Rotational equilibrium implies that the net torque on an object is zero, so it continues in its current state of angular velocity.
A pirate captain applies a torque of 3.94 Nm to a ship's wheel by using a force of 20 N at a radius of 0.2 meters.
A mechanic tightens lugs on a tire with a force of 250 N using a 0.4-meter long wrench applying a torque of 100 Nm.
The tension in a wire holding a 3 kg sign is 55 N when the net torque must be zero.
Marisa (45 kg) and Katrina (75 kg) maintain static equilibrium on a teeter-totter with Katrina sitting 0.6 meters from the fulcrum.
The force on the fulcrum from a teeter-totter with Marisa and Katrina is 1200 N.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: