What is Torque? | Physics | Extraclass.com

Extraclass Official

1 Apr 202005:21

EducationalLearning

32 Likes 10 Comments

TLDRThe video script delves into the concept of torque, a fundamental principle in physics that describes the rotational force acting on an object. It uses the analogy of opening a door to illustrate how torque is applied in everyday life, emphasizing that the force exerted on a door handle, combined with the distance from the hinge, results in the door's rotation. The script further explains torque as a vector product, perpendicular to both the position vector and the force vector, with its direction determined by the right-hand thumb rule. To solidify understanding, the video presents a problem involving a uniform wooden stick resting against a wall and the floor, demonstrating how to calculate the reaction forces and the frictional force involved. The problem-solving approach exemplifies the application of torque in static equilibrium scenarios, providing a clear and educational insight into the concept.

Takeaways

🚪 Understanding a door as a rotating object helps to comprehend how it opens and closes, rather than just seeing it as a wooden rectangle.
🌀 Torque is the rotational equivalent of force and is essential for rotating objects like doors around an axis.
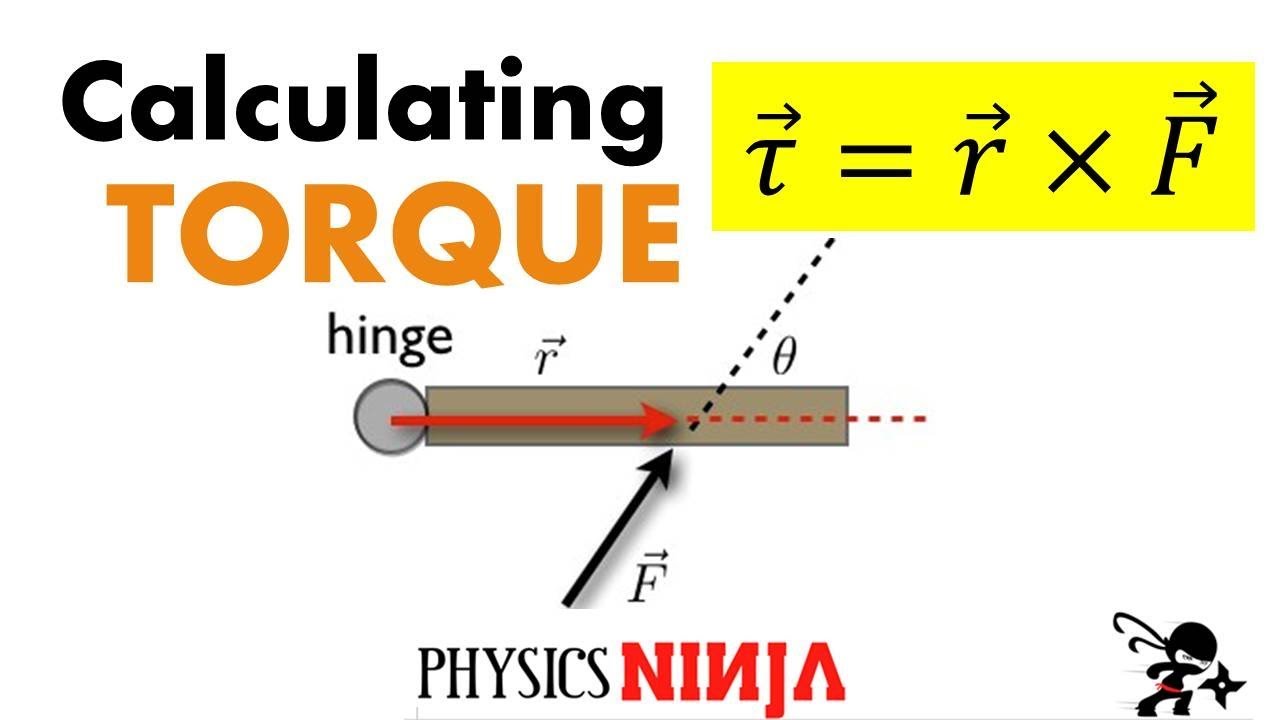
📐 The force applied to an object (like a door handle) and the distance from the axis determines the torque, which causes rotation.
⚙️ Torque is represented by the Greek symbol tau and is a vector product of the position vector and the force vector.
↗️ The direction of torque follows the right-hand thumb rule, which dictates that the thumb points in the direction of the torque when fingers align with the position vector towards the force vector.
📐 In the given example, a uniform wooden stick resting against a wall and the floor involves calculating torque and forces to understand its equilibrium.
⚖️ The reaction force of the wall on the stick is equal in magnitude to the frictional force at the bottom of the stick on the floor.
🧮 The vertical and horizontal components of the reaction force from the wall can be calculated using trigonometric functions based on the angle the stick makes with the wall.
⚛️ Equilibrium means the net torque about a point is zero, which is used to solve for unknowns in the stick scenario.
📐 The ratio of the height of the wall (H) to the length of the stick (L) can be found by analyzing the torque about the bottom of the stick.
🔢 Given the mass of the stick and the angle with the wall, the frictional force and the ratio H/L can be calculated using the principles of torque and equilibrium.
📉 The correct answer to the problem, based on the calculations, is option D, which represents the ratio H/L as 3√3/16.

Q & A

What is the primary concept being discussed in the transcript?
-The primary concept being discussed is torque, which is the rotational equivalent of force, and its application in the context of opening a door and a physical problem involving a stick leaning against a wall.
How does the door act as a rotating object?
-The door acts as a rotating object because it rotates about a fixed axis, which is the hinge, allowing the door to open by either pushing or pulling it.
What is the term used to describe the force applied to the door handle to rotate the door?
-The term used is 'torque,' which is the twisting force that causes the door to rotate around its hinge.
What is the mathematical definition of torque?
-Torque is defined as the vector product of the position vector and the force vector, resulting in a vector that is perpendicular to both the position vector and the force vector.
How is the direction of torque determined?
-The direction of torque is determined by the right-hand thumb rule, where if you align your right hand with the position vector and curl your fingers towards the force vector, your thumb points in the direction of the torque.
What is the significance of the stick example in illustrating the concept of torque?
-The stick example demonstrates how torque, or the net rotational force, can be calculated in a real-world scenario, taking into account the forces acting on the stick and its equilibrium state.
What are the forces acting on the stick in the example?
-The forces acting on the stick are its weight (mg) acting downwards, the normal reaction force from the wall, and the frictional force at the bottom of the stick on the floor.
How is the frictional force calculated in the stick example?
-The frictional force is calculated by using the horizontal component of the normal reaction force (n cos 30 degrees), which gives a frictional force of (2mg/3) * sqrt(3)/2 Newtons.
What is the relationship between the height of the wall (H) and the length of the stick (L) in the example?
-The ratio of the height of the wall (H) to the length of the stick (L) is found to be (3 * sqrt(3))/16, which is derived from the equilibrium conditions and the torque about the axis of the stick.
Why is the net torque about the axis of the stick considered to be zero?
-The net torque about the axis of the stick is considered to be zero because the stick is in equilibrium, meaning the sum of all torques acting on it must balance out.
What is the role of the right-hand rule in understanding torque?
-The right-hand rule is used to determine the direction of the torque vector. It is a standard convention that helps visualize and understand the directionality of torque in three-dimensional space.
How can one apply the concept of torque to everyday objects like doors?
-By understanding that the force applied to the door handle creates a torque that causes the door to rotate around the hinge, one can apply the concept of torque to everyday tasks, such as opening a door more efficiently by applying force closer to the hinge.

Outlines

00:00

🚪 Understanding Torque and Door Mechanics

This paragraph explains the concept of torque in the context of opening a door. It emphasizes that a door should not be viewed merely as a rectangular wooden piece but as a rotating object that pivots on a hinge. The force applied to the door handle, whether pushing or pulling, is not the sole factor in rotating the door. The distance from the axis of rotation to the point where force is applied is crucial, and this combination of force and distance is known as torque, represented by the Greek letter tau (τ). Torque is the rotational equivalent of force and is a vector perpendicular to both the position vector and the force vector. The right-hand rule is introduced to determine the direction of torque. An example is provided involving a uniform wooden stick with mass 1.6 kg leaning against a wall and resting on a rough floor, illustrating how torque and equilibrium are involved in the forces acting on the stick.

05:01

📲 Engaging with the YouTube Channel

The second paragraph serves as a call to action for viewers to interact with the content by liking, sharing, and commenting on the video. It also encourages viewers to subscribe to the YouTube channel for more educational and interesting videos. Additionally, it promotes the download of the 'Extra Class' app from the Google Play Store, which offers rewards for engagement, thereby enhancing the learning experience.

Mindmap

Keywords

💡Stork

In the context of the video script, 'stork' is not directly mentioned, but it seems to be a typographical error for 'door'. The door is discussed as a rotating object, which is a central concept in the video. The door is not to be viewed simply as a rectangular wooden piece, but as a mechanism that involves rotation about a fixed axis, the hinge. This concept is crucial for understanding the physics involved in opening a door.

💡Rotating Object

A rotating object, as mentioned in the script, is an object that spins around a fixed axis. In the context of the video, a door is considered a rotating object because it rotates on its hinges to allow entry or exit from a room. This concept is fundamental to the discussion of torque and the mechanics of opening a door.

💡Torque

Torque is defined as the rotational equivalent of force and is measured by the Greek letter tau (τ). It is the product of the force applied and the distance from the axis of rotation to the point where the force is applied. In the video, torque is used to explain how one can open a door by applying a force on the handle, which creates a twisting effect that results in the door's rotation. Torque is essential for understanding the forces involved in door mechanics.

💡Force

Force is a physical quantity that, when unopposed, will change the motion of an object. In the script, force is applied to the door handle to rotate the door. The term 'push' or 'pull' is used to denote the force exerted on the door. Force is a key component in the calculation of torque and is central to the discussion of how a door is opened.

💡Kinematics

Kinematics is a branch of physics that describes the motion of objects without considering the forces that cause the motion. The script mentions kinematics in relation to the force applied to the door handle. Understanding kinematics helps to analyze the motion of the door as it rotates around its hinges.

💡Vector Product

The vector product is a mathematical operation that takes two vectors and returns another vector. In the context of the video, torque is defined as the vector product of the position vector and the force vector. This operation is crucial for determining the direction and magnitude of the torque acting on an object, such as a door.

💡Right-Hand Thumb Rule

The right-hand thumb rule is a method to determine the direction of the torque vector. By aligning the fingers of the right hand with the position vector and curling them towards the direction of the force vector, the thumb points in the direction of the torque. This rule is used in the video to illustrate how to find the direction of torque when opening a door.

💡Uniform Wooden Stick

The script presents an example involving a uniform wooden stick with a specific mass resting against a wall. This example is used to demonstrate the principles of torque and equilibrium in a practical scenario. The stick serves as a model to apply the concepts discussed in the video to a real-world situation.

💡Inclined Manner

The term 'inclined manner' refers to the orientation of the wooden stick in the example, which is not vertical or horizontal but at an angle. This inclination is important as it affects the distribution of forces acting on the stick and is essential for the calculation of torque and the stick's equilibrium.

💡Frictional Force

Frictional force is the force that opposes the relative motion or tendency of such motion between two surfaces in contact. In the script, the frictional force at the bottom of the stick is a critical factor in maintaining the stick's equilibrium against the wall and the floor. The frictional force is calculated in the example to ensure the stick does not slide.

💡Equilibrium

Equilibrium is a state in which all forces acting on an object are balanced, resulting in no net force and no acceleration. The script discusses the stick being in equilibrium, which means the net torque about a certain point is zero. This concept is central to understanding the forces at play in the example provided in the video.

💡Extra Class App

The 'Extra Class App' is mentioned at the end of the script as a resource for more educational content. While not directly related to the main theme of physics and mechanics, it is a call to action for viewers to engage with additional learning materials, suggesting a broader context of educational resources available to the audience.

Highlights

The concept of a door is redefined, not just as a wooden rectangle but as a rotating object hinged on one side for movement.

Introduction of kinematics in practical applications, showing how the concepts of push or pull relate to force on a door's handle.

Explanation of torque as the combination of force and the distance from the axis where the force is applied.

Clarification that rotation of objects, such as doors, is governed by torque, not just by force.

Description of torque as a vector, which is perpendicular to both the position vector and the force vector.

Use of the right-hand thumb rule to determine the direction of torque.

Example problem involving a uniform wooden stick leaning against a wall, introducing concepts of reaction force and friction.

Analysis of forces acting on the stick with a breakdown of vertical and horizontal components.

Calculation of normal reaction forces and frictional force at the bottom of the stick based on given angles and mass.

Solution to find the ratio H/L using the equilibrium of torques and forces, showing the application of physics in solving real-world problems.

Demonstration that the reaction force of the wall on the stick is equal in magnitude to the reaction of the floor.

Determination of frictional force value using mass, gravity, and trigonometric calculations.

The net torque about the base of the stick is zero, indicating equilibrium.

Calculation of torque for vertical equilibrium and how it affects the stick's stability.

Conclusion that the correct option for the given problem is option D, showcasing the application of theoretical physics in exam scenarios.

Transcripts

Browse More Related Video

Torque is a Vector | Physics with Professor Matt Anderson | M12-11

torque explained

Understanding How Torque Works

Cross product and torque | Moments, torque, and angular momentum | Physics | Khan Academy

AP Physics 1 - Torque

Calculating Torque

What is Torque? | Physics | Extraclass.com

Takeaways

Q & A

What is the primary concept being discussed in the transcript?

How does the door act as a rotating object?

What is the term used to describe the force applied to the door handle to rotate the door?

What is the mathematical definition of torque?

How is the direction of torque determined?

What is the significance of the stick example in illustrating the concept of torque?

What are the forces acting on the stick in the example?

How is the frictional force calculated in the stick example?

What is the relationship between the height of the wall (H) and the length of the stick (L) in the example?

Why is the net torque about the axis of the stick considered to be zero?

What is the role of the right-hand rule in understanding torque?

How can one apply the concept of torque to everyday objects like doors?