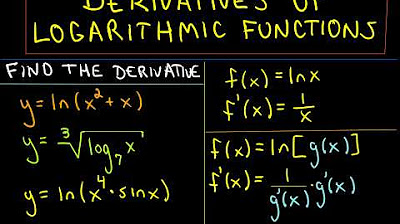Derivatives of Logarithmic and Exponential Functions

Professor Dave Explains
20 Mar 201808:41
EducationalLearning
32 Likes 10 Comments

TLDRIn this calculus video, Professor Dave derives rules for differentiating logarithmic and exponential functions. He starts with basic logarithm rules like the derivative of the natural log of x being 1/x. Using the chain rule, more complex derivatives are taken, like ln(sin(x)) = cot(x). For exponents like 2^x, the derivative rule is to bring down the natural log of the base times the original function. Towards the end, Dave shows a series representation of e^x and takes the derivative term-by-term to elegantly prove the function equals its own derivative.

Takeaways
  • 😀 We can use rules to find derivatives of logs and exponentials without derivations
  • 👍 The derivative of ln(x) is 1/x and log base a of x is 1/(ln(a) * x)
  • ✏️ Use chain rule when differentiating composite functions with logs, like ln(sin(x))
  • 📉 Derivative of a^x is ln(a)*a^x; if the exponent has x, multiply by its derivative
  • ☝️ Special case: Derivative of e^x is just e^x itself
  • 🤓 We can prove this using the factorial representation of e^x
  • 💡 Taking derivative turns the series back into itself
  • 🎯 So e^x equals its own derivative, meaning slope = function at every point
  • 🔍 This will be key when we learn integration
  • 🧠 Let's apply these rules to differentiate logs and exponentials
Q & A

  • What is the derivative of the natural log of x?

    -The derivative of the natural log of x is equal to 1/x.

  • How do you find the derivative of a logarithm with some base a?

    -Use the change of base formula to express it in terms of the natural log, then take the derivative. The final result will be 1/(ln(a) * x).

  • What is the process for differentiating a composite function involving logs, like ln(sin(x))?

    -Use the chain rule - take the derivative of the outer function (ln(x)) and multiply by the derivative of the inner function (cos(x)). This gives cotangent(x).

  • What is the derivative of e raised to the x power?

    -Remarkably, the derivative of e raised to the x power is itself. This can be proven using the factorial representation of e.

  • How do you differentiate an exponential function with a variable exponent?

    -Take the natural log of the base times the original function, then multiply by the derivative of the exponent.

  • What is the derivative rule for a general exponential A^x?

    -The derivative is equal to the natural log of A times A^x.

  • How can you differentiate log base 10 of x squared?

    -Use the chain rule - take the derivative of the outer function (1/(ln(10)*x^2)) and multiply by the derivative of the inner function (2x).

  • Why is the derivative of e^x equal to itself?

    -Graphically, this means every point on the curve is equal to the slope at that point. So the function is its own derivative.

  • What is an example of an exponential function?

    -An exponential function has the variable in the exponent, rather than a power - for example 2^x.

  • What is the overall process for differentiating logs and exponentials?

    -Apply derivative rules like the power rule and chain rule as necessary. Memorize rules for ln(x) and general exponential/log functions.

Outlines
00:00
📝 Key differentiation rules and examples

Paragraph 1 discusses several key rules for differentiating various functions like polynomials, logarithms, exponentials, etc. It provides specifics like the derivative of natural log x being 1/x, log base a of x being 1/(ln a * x), exponential function of A^x being ln A * A^x. It shows examples of applying these rules through chain rule to find derivatives of functions like ln(sin x), log10(x^2), 2^(3x+1), etc.

05:01
🔢 Proof: derivative of e^x is e^x

Paragraph 2 shows a proof that the derivative of e^x is e^x itself using the factorial representation of e. It takes the derivative of each term in the series expansion of e^x and shows the series remains unchanged, thus proving the derivative result. It notes how this makes e^x equal to its own slope at every point.

Mindmap
Keywords
💡derivative
The derivative represents the rate of change of a function. It is a core concept in calculus and differentiation. In the video, Professor Dave explains rules for taking derivatives of various functions like polynomials, logarithms and exponentials. He then applies these rules to find derivatives of composite and more complex functions.
💡chain rule
The chain rule is used to find the derivative of composite functions. As Professor Dave explains, it involves taking the derivative of the outer function and multiplying it by the derivative of the inner function. He shows examples of applying the chain rule to find derivatives like d/dx(ln(sin(x))).
💡logarithm
A logarithm represents the power to which a base number must be raised to get another number. Professor Dave reviews key rules for finding derivatives of logarithms like ln(x) and log base 10 of x. He also shows how to combine these with the chain rule.
💡exponential function
An exponential function has a variable exponent instead of a variable base. Professor Dave explains the rule for finding the derivative of exponentials like A^x, which is ln(A)*A^x. He also discusses the special case of the derivative of e^x being equal to itself.
💡e
e is an important mathematical constant, approximately equal to 2.718. Professor Dave shows a series representation for e^x and proves that its derivative is itself by taking the derivative term-by-term.
💡factorial
The factorial of a number is that number multiplied by every positive integer less than it. Professor Dave uses factorials in the series representation of e^x. The factorials cancel out when taking the derivative of this series.
💡natural logarithm
The natural logarithm has a base of e. Professor Dave states rules for finding derivatives of natural logs like ln(x) and extends it to logs of other bases using change of base formula.
💡power rule
The power rule gives a formula for differentiating functions with exponential powers, like x^n. Professor Dave uses this to find the derivative of each term in the series for e^x.
💡calculus
Calculus is the mathematical study of continuous change. Differentiation and finding derivatives are core concepts and skills in calculus covered by Professor Dave in this video.
💡cotangent
Cotangent is the reciprocal of tangent, i.e cos(x)/sin(x). Professor Dave shows that the derivative of ln(sin(x)) simplifies to cotangent x, as an example of applying the chain rule.
Highlights

The derivative of the natural log of x is equal to one over x

The derivative of any logarithm of x with some other base is one over (the natural log of that base times x)

The derivative of the natural log of a function g(x) is g'(x) over g(x)

The derivative of an exponential function A^x is equal to the natural log of A times A^x

The derivative of e^x is just e^x

A series representation of e^x can be differentiated term by term to show the derivative of e^x is itself

If a function equals its own derivative, every point on the function equals its slope at that point

The derivative of the natural log of sine x is cotangent x, by applying the chain rule

Exponential functions have the variable in the exponent, unlike polynomial functions

If the exponent of an exponential function has x, multiply the derivative by the derivative of the exponent

Log and exponential derivative rules extend differentiation to more function types

The chain rule is key for differentiating composite functions with logs and exponents

Memorizing key derivative rules saves work differentiating logs and exponents later

Derivatives of exponentials require distinguishing cases based on if x is the lone exponent

Understanding why e^x equals its own derivative leads to deeper insight about integration

Transcripts

Browse More Related Video

Derivatives of Log Functions

Derivatives of Logarithmic Functions - More Examples

Derivatives of Exponential Functions

The Derivative of ln(x) via Implicit Differentiation

Basic Derivative Rules - Part 2: Combining the Rules

Log and Exponent Derivatives | MIT 18.01SC Single Variable Calculus, Fall 2010

Rate This

5.0 / 5 (0 votes)

Thanks for rating: