Derivatives of Polynomial Functions: Power Rule, Product Rule, and Quotient Rule
TLDRThe video explains techniques for taking derivatives in calculus. It starts by reviewing the power rule and introducing notation for taking derivatives. It then covers derivatives of polynomial functions using the power rule and sum/difference rules. Next, it explains the product rule and quotient rule for finding derivatives of products and quotients of functions. Examples are provided to demonstrate application of these rules. The video emphasizes needing to memorize and practice these derivative rules diligently to be able to find the derivative of any polynomial function.
Takeaways
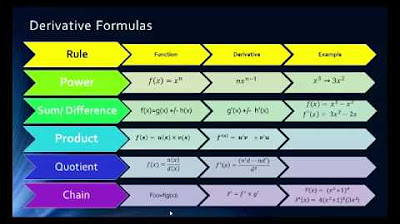
- 😀 The power rule allows us to take the derivative of a function with a positive integer exponent by pulling down the exponent as a coefficient and reducing the exponent by 1
- 😊 We can use the notation d/dx f(x) as an alternative way to represent taking the derivative of f(x) with respect to x
- 😎 The sum rule and difference rule allow us to take the derivative of a polynomial term-by-term
- 🧐 The product rule is used to take the derivative of a product of functions
- 🤓 The quotient rule, which must be memorized, is used to take the derivative of a quotient of functions
- 😕 The order of terms matters when using the quotient rule but not the product rule
- 🤩 With an understanding of these basic rules - power, sum, difference, product, and quotient - we can take the derivative of any polynomial
- 😀 Negative integer and non-integer exponents can also be handled by the power rule
- 😉 Products and quotients can get more complicated but the associated rules don't really change, just more steps
- 🥳 With practice, taking derivatives, even of complicated polynomials, is very achievable
Q & A
What is the power rule for taking derivatives?
-The power rule states that to take the derivative of a function involving a positive integer exponent, you pull the exponent down to become a coefficient and reduce the exponent by one.
How are the notations f'(x) and d/dx f(x) related?
-The notations f'(x) and d/dx f(x) are completely identical, both representing the derivative of the function f(x) with respect to x.
What is the sum rule when taking derivatives?
-The sum rule states that the derivative of f(x) + g(x) is equal to the derivative of f(x) plus the derivative of g(x), or (f+g)' = f' + g'.
What is the product rule for taking derivatives?
-The product rule states that the derivative of f(x)*g(x) is equal to f(x)*g'(x) + g(x)*f'(x).
Why can't you just multiply the derivatives when taking the derivative of a product?
-You can't just multiply the derivatives because fg' does not equal f'g'. You have to use the full product rule expression to get the correct derivative.
What is the quotient rule for taking derivatives?
-The quotient rule states that the derivative of f(x)/g(x) is equal to g(x)*f'(x) - f(x)*g'(x) all over [g(x)]^2.
Why is order important in the quotient rule?
-The order matters in the quotient rule because it involves subtraction rather than addition. Switching f'(x) and g'(x) will give an incorrect derivative.
How does the power rule apply for negative integer exponents?
-The power rule works the same for negative integer exponents - you reduce the exponent by 1 and pull the new exponent out front as a coefficient.
What makes the derivative of products and quotients more complicated?
-You can't just multiply or divide functions and use the power rule, you have to apply the specific product and quotient rules which involve more steps.
How can you become better at taking derivatives?
-Taking derivatives gets easier with diligent practice using the power, product, quotient and other rules. Identifying mistakes allows you to reinforce the proper techniques.
Outlines
😀 Introducing Power Rule for Derivatives
This paragraph introduces the power rule for taking derivatives, explaining how to use it to find the derivative of polynomial functions. It covers bringing the exponent down as a coefficient, reducing the exponent by 1, using the notations f'(x) and d/dx, and applying the power rule to examples like x^3 and 3x^4.
😊 Applying Power Rule to Polynomials
This paragraph explains how to use the power rule to take derivatives of polynomials with multiple terms, using the sum and difference rules. It provides examples of applying these rules to find derivatives term-by-term for more complex polynomial functions.
🤔 Product and Quotient Rules for Derivatives
This paragraph introduces the product rule and quotient rule for finding derivatives. It explains why fg' ≠ f'g' and provides the formulas for the product and quotient rules. Examples are shown for applying these rules to find derivatives of products and quotients of functions.
Mindmap
Keywords
💡Differentiation
💡Derivative
💡Power rule
💡Sum rule
💡Product rule
💡Quotient rule
💡Algorithm
💡Polynomial
💡Exponent
💡Calculus
Highlights
The power rule tells us that in order to take the derivative of some function involving a positive integer exponent, we just pull the exponent down to become a coefficient and then reduce the exponent by one.
d over dx followed by some function means to take the derivative of that function with respect to x.
The sum rule says that the derivative of the quantity f of x plus g of x, will be equal to the derivative of f of x plus the derivative of g of x.
No matter how many terms are in a polynomial, we will just take the derivative of one term at a time.
The product rule says that the derivative of f of x times g of x is equal to (f of x) times (g prime of x) plus (g of x) times (f prime of x).
To find the derivative of f of x over g of x, we find (g of x) times (f prime of x), minus (f of x) times (g prime of x), and all of that will be over g of x quantity squared.
For the product rule, the order of the terms didn't matter, since it involved a sum, but for the quotient rule it will matter.
If you switch the order for the quotient rule, you will get incorrect answers.
As long as we practice and become diligent, we will find that it’s not too difficult to take the derivative of any polynomial.
When using the power rule, this exponent can be a negative integer, or even a non-integer, but the rules don’t really change.
Even when products or quotients get more complicated, it’s not really any harder, just more steps, and therefore more opportunities to make a mistake.
If we practice and become diligent, we will find that it’s not too difficult to take the derivative of any polynomial.
Let's check comprehension.
Identify Highlights: Review the transcript to find the most significant findings, innovative methods, theoretical contributions, or any notable impact or practical applications.
Format into JSON: Structure the highlights and their corresponding start times into a JSON format.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: