Graphing Functions and Their Derivatives

Professor Dave Explains
5 Apr 201813:06
EducationalLearning
32 Likes 10 Comments

TLDRThe script discusses using derivatives to graph functions and get information about them. It explains how the first derivative indicates if a function is increasing or decreasing, while the second derivative shows concavity. An example plots local extrema and inflection points of a cubic polynomial using its derivatives, then sketches the function. Concepts are tied to physics of projectile motion. The goal is developing intuition for relating graphs of functions and their derivatives in order to graph and analyze functions more easily.

Takeaways
  • 😀 The derivative of a function at a point equals the rate of change of the function at that point.
  • 😯 We can sketch derivatives of functions using our understanding of rates of change, without doing algebra.
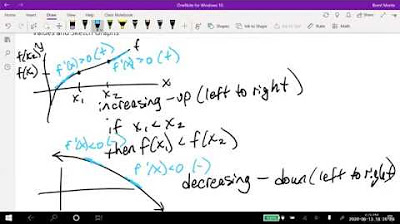
  • 📈 The sign of the first derivative tells us if a function is increasing or decreasing.
  • 😮 Zeroes of the first derivative indicate maxima and minima of the original function.
  • 📉 Zeroes of the second derivative indicate inflection points where concavity changes.
  • 👍 Positive second derivative means the function is concave up.
  • 👎 Negative second derivative means the function is concave down.
  • 🤓 We can use first and second derivatives to accurately sketch polynomials.
  • 😃 The motion of a tossed ball illustrates relationships between position, velocity and acceleration graphs.
  • 🧠 Understanding derivatives enhances our ability to analyze and graph functions.
Q & A

  • What is the derivative of a function at a particular point equal to?

    -The rate of change in the function at that point.

  • How can understanding derivatives help us graph functions?

    -It helps relate the graph of a function to the graph of its derivative. We can use information about the positive/negative values and zero crossings of the derivative to understand things like where the original function has local maxima/minima and inflection points.

  • Why is the value of a function unrelated to the rate of change of that function?

    -The value refers to the output of the function at a point, while the rate of change refers to how rapidly the output is changing. Shifting a function vertically does not change its rate of change.

  • How does the graph of position, velocity and acceleration for a ball tossed upwards relate to derivatives?

    -Position correlates with the original function, velocity is its first derivative, and acceleration is its second derivative. This shows how higher derivatives relate to the rate of change of lower derivatives.

  • What do intervals on the second derivative tell us about the original function?

    -Positive second derivative values indicate upward concavity of the original function. Negative values indicate downward concavity. Zero crossings indicate inflection points.

  • How can we find local maxima and minima of a function using derivatives?

    -By finding where the first derivative equals zero. These are points where the tangent line is horizontal.

  • What information do we need about a function to sketch its graph using derivatives?

    -The zeros of the first derivative to find extrema, zeros of the second derivative to find inflection points, end behavior, and potentially zeros of the function itself.

  • Why is a cubic function an odd function based on its first term being positive?

    -A cubic function with a positive leading coefficient will be positive for large positive x and negative for large negative x. This makes it an odd function, symmetric about the origin.

  • What changes in going from a function to its first and second derivatives?

    -The degree reduces by 1 each time we take a derivative. So a cubic function becomes quadratic, then linear, then constant for the second derivative.

  • When sketching a function using derivatives, why don't we find its zeros?

    -Finding the zeros can provide more precise graphing information, but the question says to skip this step for now since it involves older algebraic material.

Outlines
00:00
📚 Understanding Derivatives to Sketch Graphs

This paragraph explains how the derivative of a function at a point gives the rate of change, and how this concept along with concavity can be used to sketch graphs of functions and their derivatives just by reasoning about their behavior.

05:05
🏀 Relating to Projectile Motion

This paragraph provides an example relating the graphs of a quadratic function, its first derivative, and its second derivative to the position, velocity, and acceleration graphs of a ball tossed vertically, illustrating how derivatives relate rates of change.

10:11
💡 Putting it All Together

This paragraph works through finding critical points, inflection points, and end behavior of a cubic polynomial, and uses all this information along with reasoning about derivatives to accurately sketch the graph.

Mindmap
Keywords
💡Differentiation
Differentiation is the process of finding the derivative of a function. The video discusses using differentiation and derivatives to analyze and graph functions. For example, the derivative gives the rate of change of a function, which helps determine if the function is increasing or decreasing.
💡Rate of change
The rate of change refers to how rapidly a function's output value is changing with respect to its input value. Knowing the rate of change from the derivative helps analyze if a function is increasing or decreasing without needing to know if the output values themselves are positive or negative.
💡Concavity
Concavity refers to whether a curve is curved upwards (concave up) or downwards (concave down). By looking at the sign of the second derivative, you can determine concavity - positive second derivative means concave up, negative means concave down.
💡Inflection point
An inflection point is where the concavity of a curve changes from concave up to concave down or vice versa. On a graph, it's where the curve switches bend direction. It occurs when the second derivative equals zero, meaning the first derivative is changing sign.
💡Local extrema
Local extrema refer to the maximum and minimum points on a graph. By setting the first derivative equal to zero to find critical points and plugging them into the original function, you can locate local maximums where the function curves downwards and local minimums where it curves upwards.
💡End behavior
A function's end behavior refers to the trend of how it progresses as the input increases or decreases towards positive or negative infinity. Knowing end behavior contributes to sketching an accurate overall graph.
💡Tangent line
A tangent line touches a function's graph at only one point. The slope of the tangent line equals the value of the derivative at that point. Horizontal tangent lines indicate local maximums or minimums where the derivative is 0.
💡Polynomials
Polynomial functions involve terms with integer powers and coefficients. The video shows how analyzing derivatives helps graph higher degree polynomial functions beyond just basic algebraic methods.
💡Motion
The video relates position, velocity and acceleration graphs to visualizing differentiation. For example, velocity is the derivative of position. Knowing derivatives helps qualitatively analyze motion.
💡Curve sketching
Using information from derivatives, including rate of change, concavity, inflection points and local extrema, assists with accurately sketching the curve of a function by determining where it increases/decreases as well as changes convexity.
Highlights

The derivative of a function at a point is equal to the rate of change of the function at that point

The value of a function and the rate of change of that function are totally unrelated

The shape of the curve, not vertical shifts, determines the derivative

Graphs of derivatives illustrate motion concepts like position, velocity and acceleration

If the derivative is positive, the function is increasing; if negative, decreasing

Zeros of the derivative indicate maxima and minima of the original function

Inflection points occur where the second derivative is zero

Positive second derivative regions are concave up; negative regions are concave down

Find local extrema by finding zeros of the first derivative

Inflection points occur where the second derivative is zero

Use first and second derivative information to accurately graph polynomials

Cubic functions with positive leading terms rise from negative infinity to positive infinity

Passing through inflection points changes concavity of function graphs

Local extrema represent points where graphs change direction

Derivatives reveal graph details beyond typical algebraic graphing methods

Transcripts

Browse More Related Video

3.2 - Using Second Derivatives to Classify Max and Min Values

Calculus 1 Lecture 3.4: The Second Derivative Test for Concavity of Functions

Math 11 - Section 3.2

Concavity introduction | Using derivatives to analyze functions | AP Calculus AB | Khan Academy

Math 11 - Section 3.1

Business Calculus - Math 1329 - Section 3.2 - Concavity and Points of Inflection

Rate This

5.0 / 5 (0 votes)

Thanks for rating: