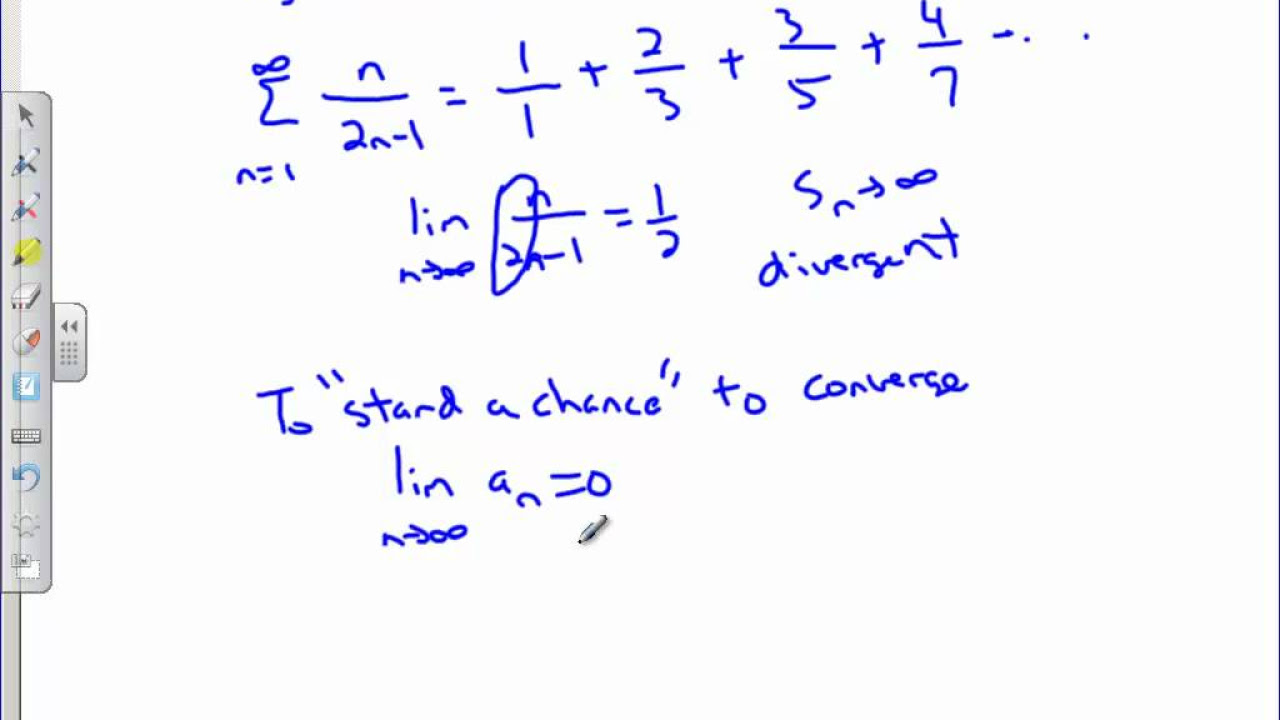Convergence and Divergence: The Return of Sequences and Series
TLDRThe script discusses mathematical sequences and series, explaining key concepts like convergence, divergence, and summation notation. It provides examples of different types of sequences, distinguishing between those that converge to a finite limit or diverge to infinity. Connections are then made to infinite series, assessing convergence based on the behavior of the sequence generating the series. Techniques like algebraic manipulation and theorems like the squeeze theorem are noted as tools for evaluating tricky series. Overall, the goal is to build an understanding of convergence to then apply to more advanced math topics.
Takeaways
- 😀 A sequence is a list of numbers that follows a particular pattern or rule.
- 😇 We can assess if a sequence is convergent or divergent by looking at its limit as N approaches infinity.
- 🧐 A sequence is convergent if its limit exists and is a finite number. It is divergent otherwise.
- 🤓 Techniques like L'Hospital's rule and the squeeze theorem can help determine convergence.
- 🤯 An infinite series is the sum of all terms in an infinite sequence.
- 😮💨 A series can also be convergent or divergent, based on whether the sequence terms add up to a finite sum.
- 😲 A necessary but not sufficient condition for convergence is that the sequence limits to 0.
- 😀 For geometric series, convergence depends on whether |R| is less than, equal to, or greater than 1.
- 🥳 Manipulating a series term into an equivalent form can help assess convergence by inspecting limits.
- 🤠 Understanding convergence/divergence of sequences and series sets the stage for more advanced series work.
Q & A
What is the definition of a convergent sequence?
-A convergent sequence is one that asymptotically approaches some finite number as N approaches infinity. If the limit exists, the sequence is convergent.
What is an example of a divergent sequence?
-The sequence A_N = N is a divergent sequence, since as N approaches infinity, the terms approach infinity as well, so there is no finite limit.
What is the squeeze theorem?
-The squeeze theorem states that if there are three sequences A, B, and C, where B is always between A and C, and if A and C both converge to the same limit L, then B must also converge to L.
What is the requirement for a series to be convergent?
-In order for a series to be convergent, the sequence that generates the terms in the series must have a limit of zero.
When is a geometric series convergent?
-A geometric series with first term A and common ratio R is convergent when the absolute value of R is less than 1. In that case, the sum of the series is A/(1-R).
How can you show a series is divergent without summing the terms?
-You can show a series is divergent by showing the sequence used to generate the terms does not converge to zero, since that is a requirement for convergence.
What is an example of a convergent infinite series?
-The series 1/2 + 1/4 + 1/8 + ... is a convergent infinite series. The sequence of partial sums approaches 1, so the series converges to 1.
What is the difference between a sequence and a series?
-A sequence is an infinite list of terms, while a series is the sum of the terms of an infinite sequence.
What is improper summation notation?
-Improper summation notation, like the upper case sigma, is used to represent infinite series as a compact summed expression rather than writing out all the terms.
What is the concept of a limit as it applies to sequences and series?
-We analyze the limit of a sequence as N approaches infinity to determine if the sequence converges. For series, we care about whether the sequence of partial sums converges to a finite limit.
Outlines
😊 Introducing Sequences and Convergence/Divergence of Series
This paragraph introduces the concept of sequences, including arithmetic, geometric, and Fibonacci sequences. It discusses how sequences can be represented with formulas and expanded into series with summation notation. The concepts of convergent and divergent sequences are explained - a convergent sequence approaches a finite limit, while a divergent one does not. Some techniques for assessing convergence are noted, like L'Hospital's rule and the squeeze theorem.
😮 Examples of Convergent and Divergent Series
This paragraph provides examples to illustrate convergent and divergent series. The series of positive integers is shown to be divergent. However, some infinite series like 1/2^N can converge to a finite value. Requirements for convergence of geometric series and general series are discussed. A test case of a series derived from a sequence that does not converge to 0 is analyzed to demonstrate divergence.
Mindmap
Keywords
💡sequence
💡convergent
💡divergent
💡series
💡limit laws
💡geometric series
💡summation notation
💡improper integrals
💡theorem
💡manipulation
Highlights
We want to assess whether a sequence is convergent or divergent.
If the limit exists, as a finite number, we call this sequence convergent.
Sometimes we can use special techniques, like L'Hospital's rule or the squeeze theorem.
If the sequence asymptotically approaches some finite number, it is convergent. If it does not do that, it is divergent.
When we try to add up all the terms in an infinite sequence, we get an infinite series.
We can talk about convergent and divergent series just like we did for sequences.
Different types of series will have different requirements for convergence.
In order for a series to be convergent, the sequence generating the terms must have a limit of zero.
Even if the limit of the sequence is zero, it is still not a guarantee that the related series will converge.
We can look at a series and state that it is divergent by showing the sequence it derives from does not converge to zero.
Now that we understand convergence and divergence for sequences and series, we are ready to move forward and learn more about series.
Let's apply this understanding to series. First we have to recall what a series is.
This makes sense, because if the limit were any other number, there would be no way for the terms in the series to add up to a finite value.
If equal to one, we are just adding up infinitely many A terms, which will also be divergent.
But if the absolute value of R is less than one, each term will get smaller, and the limit of the sequence will be zero.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: