Three-Dimensional Coordinates and the Right-Hand Rule
TLDRThe script introduces the concept of three-dimensional coordinate systems, building on the two-dimensional coordinate plane by adding a z-axis perpendicular to the x-y plane. It explains how points in 3D space are specified using ordered triples, with x, y, and z coordinates, and how the right-hand rule determines positive/negative directions. Key ideas covered include the three coordinate planes, division into octants, representing points algebraically, the distance formula generalized to 3D, and using 3D coordinates. The goal is to provide the mathematical foundation for working with three spatial dimensions as commonly experienced.
Takeaways
- 😀 We are moving from 2D coordinate planes to 3D coordinate systems by adding a Z-axis perpendicular to the X and Y axes
- 👍 A point in 3D space is described by an ordered triple giving the X, Y, and Z coordinates
- ✅ The right-hand rule helps determine the positive direction of each axis
- 💡 3D space has 3 coordinate planes (XY, XZ, YZ) and is divided into 8 octants
- 📏 The distance formula is extended to 3D by adding the difference in Z coordinates squared
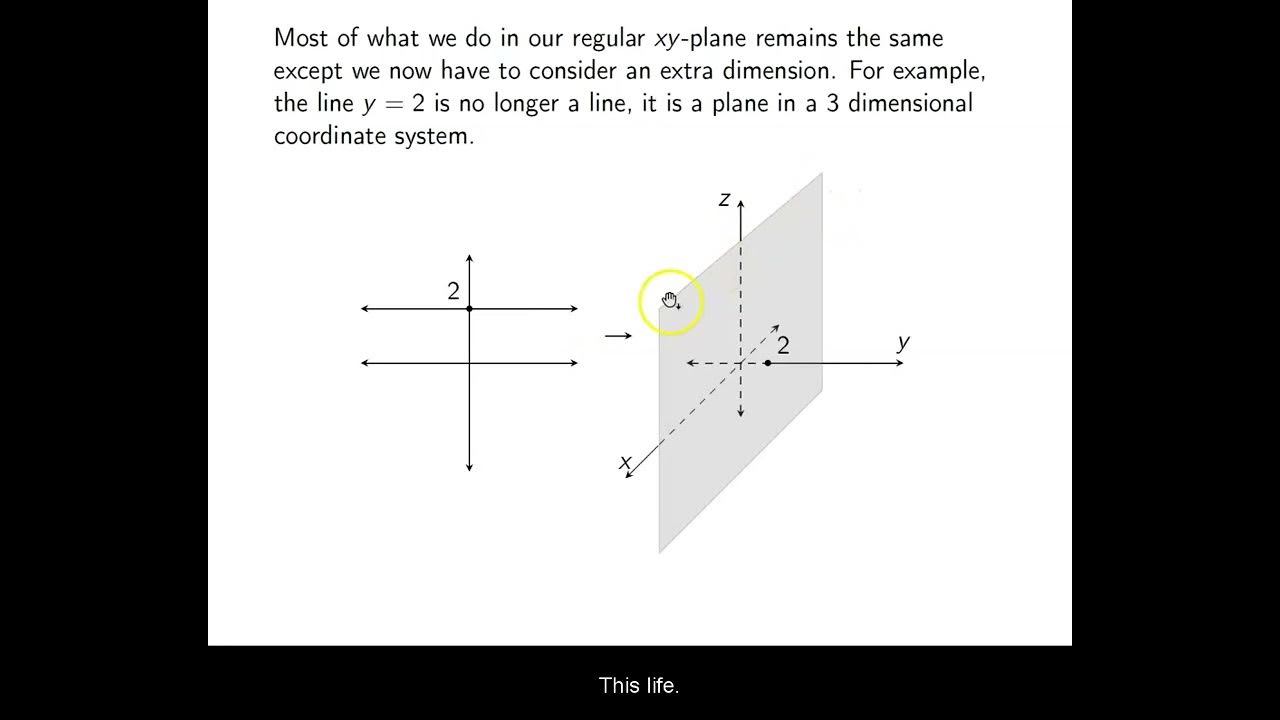
- 🔎 Planes in 3D space can be created by holding one variable constant
- 🚩 The intersection of two non-parallel planes gives a line
- 🤔 Lines in 3D space can be represented algebraically in various ways, including with vectors
- 🧮 We can still use the Pythagorean Theorem to derive formulas like the 3D distance formula
- 👽 Visualizing 3D structures in 2D can be tricky but is often possible using lines, boxes, etc.
Q & A
What is needed to generate a three-dimensional space from a two-dimensional coordinate plane?
-To generate a three-dimensional space, you simply have to add a third axis, a Z axis, which is perpendicular to the plane containing the X and Y axes.
How is a point described in two dimensions versus three dimensions?
-In two dimensions, a point is described with an ordered pair, giving the X and Y coordinates. In three dimensions, a point is described with an ordered triple, giving the X, Y, and Z coordinates.
What is the right-hand rule and how does it relate to setting up the axes?
-The right-hand rule tells us how to orient the three axes properly. If you curl your right hand around the Z-axis with your fingers going counterclockwise from the positive X to positive Y axis, then your thumb points in the positive direction of the Z-axis.
What are the three coordinate planes in three-dimensional space?
-The three coordinate planes in three-dimensional space are the XY plane, XZ plane, and YZ plane. Each plane contains the two axes listed.
How is space divided up in three dimensions?
-In three dimensions, space is divided up into eight octants, with the first octant being where the X, Y and Z values are all positive.
How can a constant value assigned to a variable represent geometrically?
-Assigning a constant value to one variable in two dimensions produces a line. In three dimensions, it produces a plane.
How can two non-parallel planes intersect?
-Two non-parallel planes intersect at a line.
What is the distance formula between two points in three dimensions?
-The distance formula is: sqrt[(X2 - X1)2 + (Y2 - Y1)2 + (Z2 - Z1)2]
How is the three-dimensional distance formula derived?
-It's derived by drawing a box between two points with the points as opposite corners, applying the Pythagorean Theorem to the triangles formed inside to get the diagonal distance.
What is the distance between the points (2, -1, 7) and (1, -3, 5)?
-Plugging the coordinates into the formula: sqrt[(2 - 1)2 + (-1 - -3)2 + (7 - 5)2] = sqrt[1 + 4 + 4] = sqrt[9] = 3
Outlines
📏 Introducing 3D Coordinate Systems
This paragraph introduces the concept of 3D coordinate systems by starting with the familiar 2D coordinate plane and adding a third perpendicular Z axis to create a 3D space. It explains that points in 3D space are described using ordered triples giving the X, Y, and Z coordinates. It also covers concepts like the right-hand rule for orienting the axes, coordinate planes in 3D, and division of space into octants.
😀 Calculating Distances Between Points in 3D
This paragraph presents the formula for calculating the distance between two points P1 and P2 in 3D space. By drawing a box between the points and applying the Pythagorean theorem, the formula is derived. An example calculating the distance between the points (2, -1, 7) and (1, -3, 5) is shown, resulting in an answer of 3.
Mindmap
Keywords
💡coordinate plane
💡three-dimensional space
💡ordered triple
💡right-hand rule
💡coordinate planes
💡octants
💡distance formula
💡planes
💡vectors
💡Pythagorean Theorem
Highlights
To generate a three-dimensional space, we simply have to add a third axis, a Z axis, which is perpendicular to the plane containing the X and Y axes.
Whereas a point on a plane can be described with an ordered pair, in space, we will need an ordered triple, where three numbers give us the X, Y, and Z coordinates of the point.
This tells us that if you have the three axes, but you want to determine which direction on each axis is positive or negative, simply curl your hand around the Z-axis.
First, there are now three coordinate planes instead of one. Those are the XY, XZ, and YZ planes, which each contain the two axes listed.
Space is divided up into eight octants, with the first octant being the one where X, Y, and Z values are all positive.
In addition, whereas assigning a constant value to one of these variables would produce a line in the two-dimensional coordinate plane, doing so in three-dimensional space will produce a plane.
The intersection of two planes, so long as they are not parallel, will give us a line, and there are a number of ways a line can be represented algebraically, including with vectors.
We can find the distance between two points in space using a formula analogous to the distance formula in two dimensions, with the addition of a term for the Z-coordinate difference.
The length of the diagonal line connecting two points, or the distance between them, is given by the 3D distance formula.
We can arrive at the 3D distance formula by applying the Pythagorean Theorem to triangles drawn between the points within an imaginary box.
Let's call these two points A and B. (P one P two) quantity squared is equal to (P one B) quantity squared plus B P two quantity squared.
(P one B) quantity squared, in turn, is equal to (P one A) quantity squared plus AB quantity squared.
So we can make the substitutions to get the final 3D distance formula.
To find the distance between two 3D points, plug their coordinates into this formula, evaluate the differences, square them, sum them, and take the square root.
3 is the distance between the example points (2, -1, 7) and (1, -3, 5) when calculated using the 3D distance formula.
Transcripts
Browse More Related Video

Calculus 3: Three-Dimensional Coordinate Systems (Video #1) | Math with Professor V
Ch. 9.3 Three Dimensional Coordinate Geometry

Midpoint in 3D Space (Calculus 3)

Calculus 3 Lecture 11.2: Vectors in 3-D Coordinate System
Engineering Mechanics: Statics Lecture 4 | Cartesian Vectors in 3D

Intercepts and Traces of Surfaces (in 3D Space)
5.0 / 5 (0 votes)
Thanks for rating: