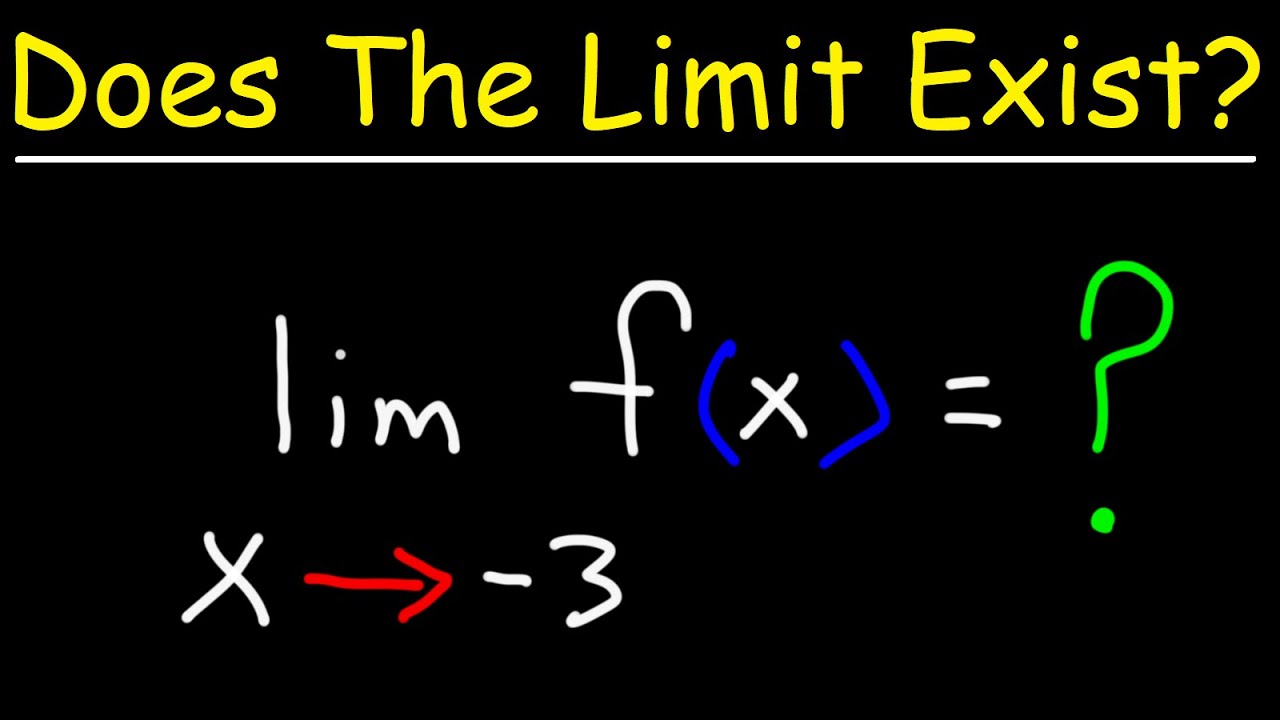Limits and Limit Laws in Calculus
TLDRThe video explains the concept of limits in calculus, including how to evaluate limits, where they are useful when functions have discontinuities, and important limit laws for manipulating expressions. It covers basic examples like limits of polynomial functions, more complex examples like sine of x over x as x approaches 0, and directional one-sided limits. After establishing this foundation, it transitions to a framework beyond limits to understand derivatives and integration.
Takeaways
- 😀 Limits describe the behavior of a function as its input approaches a particular value, even if the function is undefined at that value.
- 👉🏻 Limits help analyze functions with discontinuities or vertical asymptotes.
- 📈 Limit laws allow algebraic manipulation of limits, like sums, differences, products and quotients of limits.
- 🔢 The limit of a continuous function as x approaches a equals f(a).
- ⚠️ A limit may not exist if the left-hand and right-hand limits differ.
- 🤔 Even if a function is undefined at a point, its limit at that point may exist.
- 😮 The limit of sine(x)/x as x approaches 0 is 1, despite 0/0 being undefined.
- 📉 Limits characterize end behavior of functions as inputs trend to positive or negative infinity.
- ↔️ Context of limits gives way to more modern framework for understanding derivatives and integrals.
- 🏁 With limit fundamentals covered, it's time to move on to learning about derivatives.
Q & A
What is a limit in calculus?
-A limit describes the value that a function approaches as the input approaches some value. It allows us to analyze a function's behavior near discontinuities or asymptotes.
When are limits useful in calculus?
-Limits are useful when dealing with functions that have discontinuities or vertical asymptotes. They allow us to understand the function's behavior as it approaches these special points.
What is an example of a limit law in calculus?
-An example of a limit law is that the limit of a sum of functions equals the sum of the limits. So if f(x) approaches 3 and g(x) approaches 5 as x approaches 2, then f(x)+g(x) approaches 3+5=8 as x approaches 2.
What is the difference between a left-hand and right-hand limit?
-A left-hand limit describes the function's behavior as the input approaches some point from the left or from smaller values. A right-hand limit describes the behavior as the input approaches the point from the right or from larger values. The two can differ for functions with discontinuities.
What does it mean when a limit does not exist?
-When a limit does not exist at some point, it means the function's behavior differs depending on whether the point is approached from the left or from the right. The left and right handed limits are not equal.
What is an example of a function with an asymptote?
-An example would be f(x) = 1/x which has a vertical asymptote at x=0. The limit describes what 1/x approaches from both sides as x approaches 0, even though 1/0 is undefined.
How can limits help evaluate 0/0?
-If a function contains 0/0, limits allow you to understand what the function value approaches by substituting values closer and closer to but not equal to 0. This avoids actually dividing by 0 while revealing the behavior.
What does it mean for a function to be continuous?
-A continuous function is one where the limit of f(x) as x approaches a equals f(a) for all values of a in the domain. There are no jumps, asymptotes, or places where the function is undefined.
What is the advantage of using limit laws algebraically?
-The limit laws allow you to evaluate complex limits algebraically rather than by graphing. You can break the expression down into simpler pieces, evaluate the limits of those, then combine them using the rules.
How are derivatives related to limits?
-The derivative of a function at a point is defined as the limit of the slope of secant lines as the distance between points along the function approaches 0. So derivatives rely on limits.
Outlines
📘 Defining and Understanding Limits
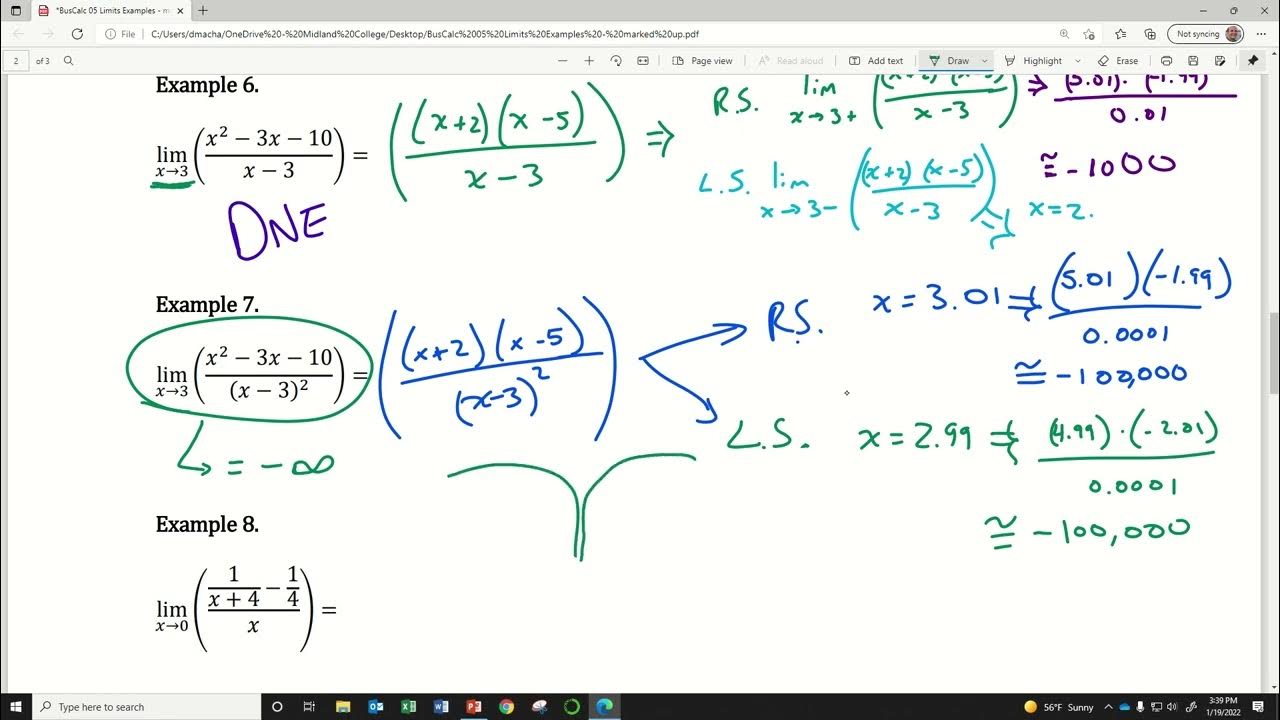
This paragraph introduces the concept of limits in calculus. It explains how limits describe the behavior of a function as the input approaches a particular value, especially values where the function is discontinuous or undefined. Examples of using limits are given, including finding vertical asymptotes, analyzing end behavior, and handling indeterminate forms like 0/0.
👆 Evaluating One-Sided Limits and Limit Laws
This paragraph discusses evaluating one-sided or directional limits, which can be different coming from the left or right. It then covers basic limit laws for sums, differences, products, quotients, powers, roots, and constants. These laws allow for manipulating and evaluating limits algebraically.
🧮 Applying Limit Laws to Complex Examples
This paragraph shows how to use the limit laws to evaluate the limit of a complex rational function as x approaches -2, without having to graph the function. This demonstrates how the laws allow limits to be found algebraically.
Mindmap
Keywords
💡limits
💡continuity
💡derivatives
💡integrals
💡asymptotes
💡discontinuities
💡end behavior
💡one-sided limits
💡limit laws
💡cancellation of terms
Highlights
Limits describe what a function does as it approaches a particular value, even if the function is undefined at that value.
Limits allow us to understand the end behavior of a function as x approaches positive or negative infinity.
Some functions have discontinuities where limits let us understand the function's behavior as we approach that point.
Limits help us evaluate more complex functions like 0/0 cases where simply plugging in values doesn't work.
A function's limit may depend on whether we approach from the left or right side.
We can manipulate and evaluate limits algebraically using laws like the limit of sums and quotients.
The limit laws allow us to break down complex limit problems instead of graphing the function.
Understanding limits prepared us for learning about derivatives in a modern framework.
Vertical asymptotes show why we need to understand limits instead of simply plugging in values.
Point discontinuities demonstrate cases where limits help assess function behavior.
Trigonometric functions like sine provide insightful limit evaluation cases.
Step functions have different one-sided limits approaching from left vs. right.
Sum and difference rules allow combining function limits using basic arithmetic.
Power rule relates limits and exponents for efficient evaluation.
The limit laws transform complex limits into more manageable forms.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: