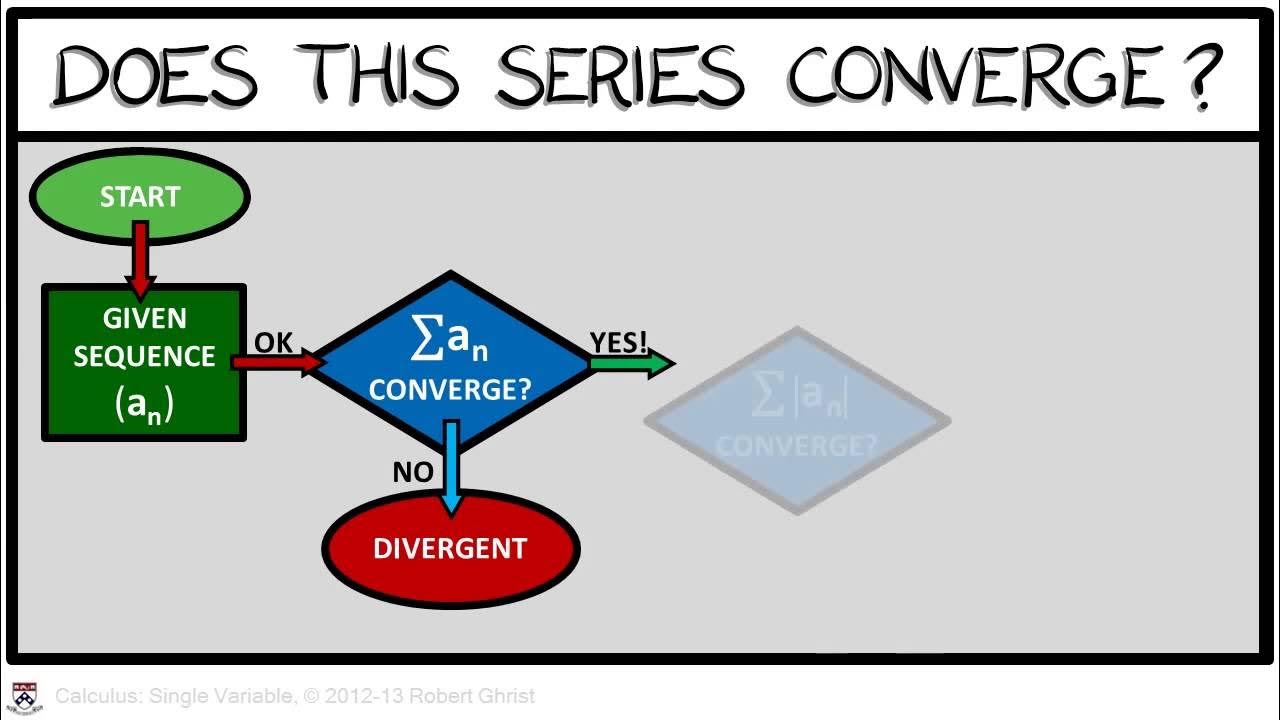
Alternating Series, Types of Convergence, and the Ratio Test

Professor Dave Explains
6 Jul 201812:08
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains alternating series, where the signs of terms alternate between positive and negative. It shows how to produce such series using expressions with negative one raised to a power involving n. It introduces the alternating series test to assess convergence. It also distinguishes between absolute convergence, where taking the absolute value results in a convergent series, vs conditional convergence. Finally, it demonstrates the ratio test to determine if a series is absolutely convergent.

Takeaways
  • 😀 An alternating series has positive and negative terms that alternate in sign.
  • 😮‍💨 An alternating series often involves (-1)^n or a similar term that alternates between +1 and -1.
  • 👍 The alternating series test helps determine if an alternating series converges.
  • 😊 An alternating series converges if the terms decrease in absolute value to 0.
  • 🧐 Absolute convergence means both the original series and its absolute value converge.
  • 😲 Conditional convergence means the series converges but its absolute value diverges.
  • 🔎 The ratio test helps determine if a series is absolutely convergent.
  • 🤓 Clever algebraic manipulation is needed with the ratio test.
  • 🤔 The ratio test says: if the limit < 1, absolute convergence. > 1, divergence.
  • 😕 Some series that seem like they should converge turn out to diverge.
Q & A

  • What is an alternating series?

    -An alternating series is one in which the signs of the terms alternate between positive and negative values.

  • How can you produce an alternating series?

    -You can produce an alternating series by including a term where negative one is raised to some exponent involving N, such as negative one to the N minus one power.

  • What is the alternating series test?

    -The alternating series test states that if each term in the series is smaller than the last, disregarding sign, and if the sequence goes to zero in the limit, then the alternating series will converge.

  • What is the difference between absolute convergence and conditional convergence?

    -If an alternating series and its absolute value series are both convergent, it is absolutely convergent. If the absolute value series diverges but the original series converges, it is conditionally convergent.

  • What is the ratio test?

    -The ratio test takes the limit as N approaches infinity of the absolute value of A_(N+1)/A_N. If the limit is less than 1, the series converges. If greater than 1, it diverges. If equal to 1, no conclusion can be made.

  • When using the ratio test, why did we take the reciprocal of the fraction?

    -Taking the reciprocal allowed us to flip the fraction so we could cancel out terms and simplify the expression.

  • Why did we use properties of exponents to break down (N+1)^(N+1)?

    -Using properties of exponents allowed us to separate the terms so we could cancel the N+1 terms in the numerator and denominator.

  • Why does an alternating series with 1/N diverge when taking the absolute value?

    -Taking the absolute value turns it into a p-series with p=1. Any p-series with p<=1 is divergent, so the absolute value diverges.

  • What happens when the ratio test gives a limit of 1?

    -If the ratio test limit equals 1, then the test is inconclusive and cannot determine convergence or divergence of the series.

  • In the last example, why did we recognize 1+1/N as e?

    -1+1/N is the mathematical definition of the constant e. Since e is greater than 1, the ratio test showed the series diverges.

Outlines
00:00
😃 Alternating Series and Convergence

Introduces alternating series where signs alternate between positive and negative. Mentions the alternating series test to assess convergence. Provides examples of alternating series and determines if they converge based on the test criteria.

05:02
😊 Absolutely and Conditionally Convergent Series

Distinguishes between absolutely convergent and conditionally convergent series. Absolutely convergent series have both the original and absolute value of series convergent. Uses ratio test to determine if a series is absolutely convergent.

10:06
🙂 Comprehension Check on Alternating Series

Summarizes key learnings on alternating series and prompts readers to check their comprehension.

Mindmap
Keywords
💡alternating series
An alternating series is a series where the terms alternate between positive and negative values. This makes assessing convergence tricky. An example is (-1)^(n-1)/n which alternates between 1, -1/2, 1/3 etc. This relates to testing different types of series for convergence.
💡absolutely convergent
A series that is convergent, and its absolute value is also convergent. This means taking the absolute value of each term does not affect convergence. An example is (-1)^(n-1)/n^2 which is absolutely convergent.
💡conditionally convergent
A series that is convergent, but taking the absolute value results in a divergent series. This means convergence depends on the alternating signs. An example is (-1)^(n-1)/n which is conditionally convergent.
💡alternating series test
A test to assess convergence of alternating series. States that if terms decrease in absolute value and limit to 0, the series converges. Used to show (-1)^(n-1)/sqrt(n) converges.
💡ratio test
A test for absolute convergence by taking the limit of the ratio of consecutive terms. If less than 1, absolutely convergent. If greater, divergent. Used to show n^n/n! diverges.
💡arithmetic sequence
A sequence where the difference between consecutive terms is constant. Contrasted with alternating and geometric sequences when introducing series.
💡geometric sequence
A sequence where each term after the first is obtained by multiplying the previous one by a constant. Contrasted with arithmetic and alternating sequences when introducing series.
💡convergence
When the limit of a series equals some finite number as n approaches infinity. Important concept for assessing different types of series.
💡divergence
When the limit of a series is infinity or does not exist. Important concept contrasted with convergence when assessing series.
💡p-series
A series with terms represented by 1/n^p. Used when taking the absolute value of (-1)^(n-1)/n to get a p-series with p=1 which diverges.
Highlights

An alternating series is one in which the signs of the terms alternate between positive and negative values.

In order to produce an alternating series, there will usually be a term whereby the number negative one is raised to some exponent.

The alternating series test provides criteria to assess convergence for alternating series.

If each term in the series is smaller than the last and the sequence goes to zero, the alternating series converges.

Slight changes in the exponent associated with the negative one term do not affect convergence.

If a series and its absolute value series are both convergent, the original series is absolutely convergent.

If a series converges but its absolute value diverges, the original series is conditionally convergent.

The ratio test helps determine if a series is absolutely convergent by taking the limit of the ratio of consecutive terms.

If the limit from the ratio test is less than 1, the series is absolutely convergent.

If the limit equals 1, the ratio test provides no information about convergence.

The ratio test involves creating a fraction with the n+1 term over the nth term and simplifying.

Factorial and power properties can help simply ratio test fractions.

Recognizing a simplified ratio as a known constant like e allows conclusions about convergence.

Now we can test alternating series for different types of convergence using several methods.

These tools help assess if an alternating series converges absolutely, conditionally, or diverges entirely.

Transcripts

Browse More Related Video

Absolute and Conditional Convergence

AP Calculus BC Lesson 10.9

Calculus Chapter 5 Lecture 53 Absolute & Conditional

Calculus 2 Lecture 9.6: Absolute Convergence, Ratio Test and Root Test For Series

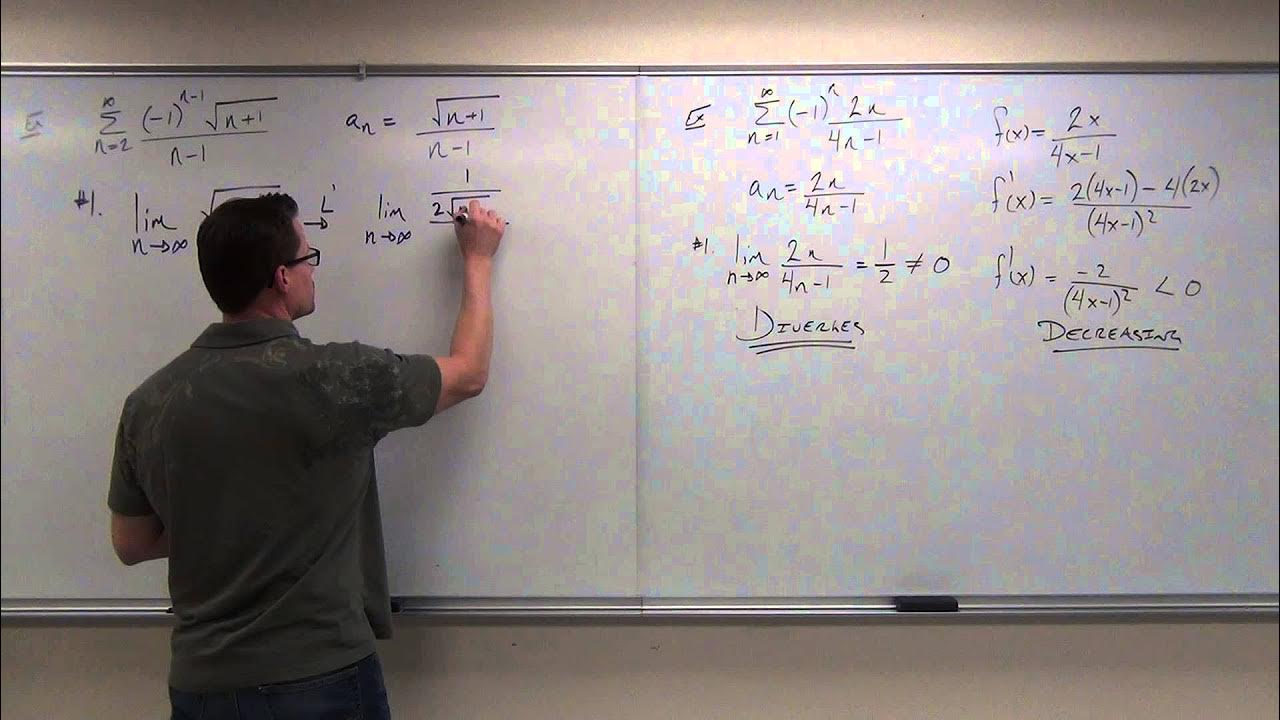
Calculus 2 Lecture 9.5: Showing Convergence With the Alternating Series Test, Finding Error of Sums

Unit VII: Lec 3 | MIT Calculus Revisited: Single Variable Calculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating: