Torque Introduction

Flipping Physics
7 Oct 201809:58
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the concept of torque is introduced and explained through the examination of translational and rotational motion. The discussion includes the definition of torque as rotational force, its relationship with force and the moment arm, and how it causes angular acceleration. The video uses relatable examples, such as opening a door, to illustrate how the position and angle of force application affect torque, emphasizing the importance of the moment arm and the sine of the angle in calculating torque. The units of torque are also clarified, distinguishing it from work and energy.

Takeaways
  • 📚 Torque is the rotational equivalent of force and is defined as the ability of a force to cause angular acceleration.
  • 🔩 The symbol for torque is the lowercase Greek letter tau (τ), which resembles a curly 't'.
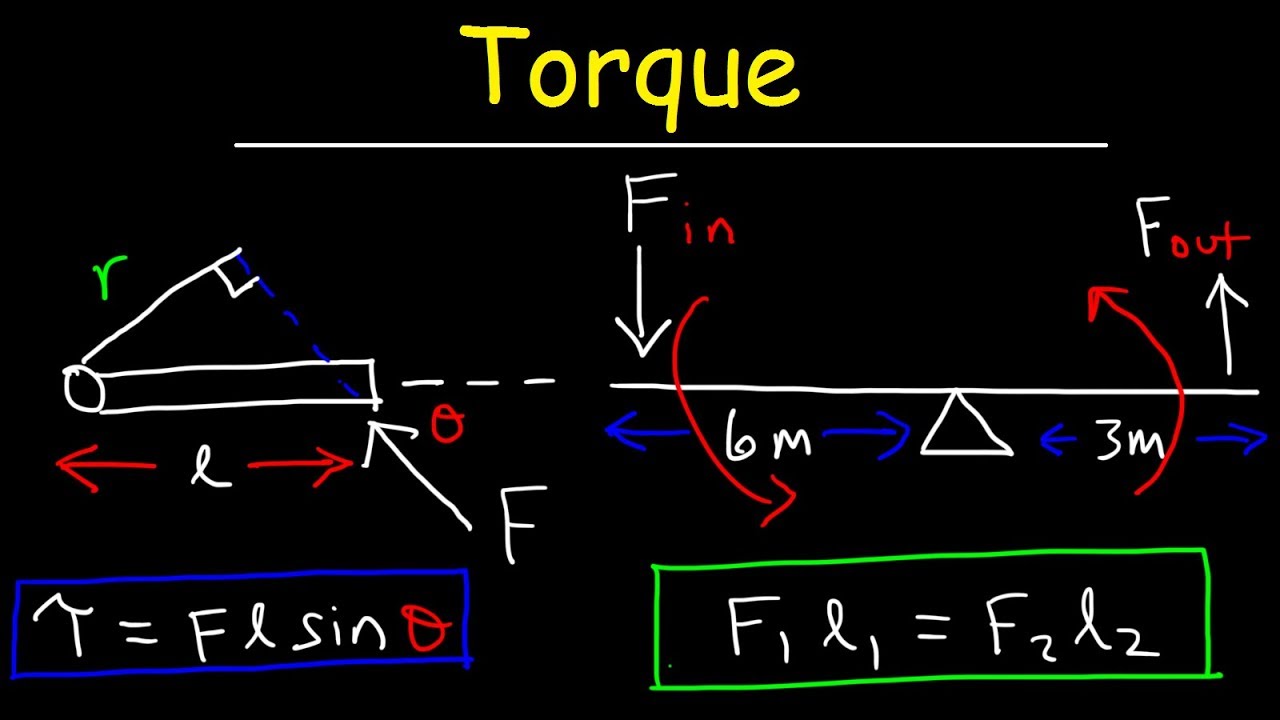
  • 📐 The formula for torque is τ = r * F * sin(θ), where 'r' is the moment arm, 'F' is the force, and 'θ' is the angle between the force vector and the moment arm.
  • 🚴 The bicycle wheel examples illustrate the differences between translational motion (center of mass moving), rotational motion (spinning around the center of mass), and when an object has both types of motion.
  • 🤸‍♂️ Translational motion is when the entire object moves from one place to another, as in the center of mass moving.
  • 🎡 Rotational motion is when an object moves in a circular path around its center of mass, like a spinning wheel.
  • 🚪 Understanding torque is related to everyday experiences, such as opening doors; pushing near the handle (far from the hinge) applies a larger torque, making it easier to open the door.
  • 🔄 The maximum torque is achieved when the force is applied perpendicular to the moment arm (90 degrees between the force vector and the moment arm).
  • 📐 The moment arm (or lever arm) is the perpendicular distance from the axis of rotation to the line of action of the force.
  • 🔢 The units for torque are newton-meters (Nm), which are different from the units for work and energy (joules, J), emphasizing that torque is a vector quantity, unlike work and energy which are scalars.
  • 🤔 The concept of supplementary angles is introduced to explain that the sine of angles that add up to 180 degrees (like 90+x and 90-x) have the same value, which is relevant when calculating torque with different angles.
Q & A

  • What is the main topic of the transcript?

    -The main topic of the transcript is the concept of torque, its definition, and its relation to translational and rotational motion.

  • What is translational motion?

    -Translational motion is when the center of mass of an object moves from one place to another.

  • What is rotational motion?

    -Rotational motion is when an object moves in circles around its center of mass.

  • Can an object have both translational and rotational motion at the same time?

    -Yes, an object can have both translational and rotational motion simultaneously.

  • What is the definition of torque?

    -Torque is the ability of a force to cause angular acceleration, which is essentially rotational force.

  • What is the symbol and formula for torque?

    -The symbol for torque is the lowercase Greek letter tau (τ), and the formula is τ = r × F × sin(θ), where r is the moment arm, F is the force causing the torque, and θ is the angle between the force vector and the r vector.

  • Why is it more effective to apply force near the handle when opening a door?

    -Applying force near the handle is more effective because it maximizes the moment arm (r), leading to a larger torque and thus a greater ability to cause angular acceleration, making it easier to open the door.

  • Why pushing at an angle is not effective in opening a door?

    -Pushing at an angle is not effective because the angle between the force direction and the r vector is not 90 degrees, resulting in a smaller sine value and therefore a smaller torque, reducing the ability to cause angular acceleration.

  • What happens when you push on the side of the door?

    -When you push on the side of the door, the angle between the r vector and the force is either 180 degrees (for a push) or 0 degrees (for a pull), both of which have a sine value of zero, resulting in no torque and no ability to cause angular acceleration of the door.

  • What is the moment arm in the context of torque?

    -The moment arm, also known as the lever arm, is the perpendicular distance between the line of action of the force and the axis of rotation. It is the component of the position vector (r) that is perpendicular to the extension line of the force.

  • What are the units for torque?

    -The units for torque are newton meters (Nm), which is different from the units for work and energy (joules) to distinguish torque as a vector quantity from work and energy, which are scalars.

Outlines
00:00
📚 Introduction to Torque and Motion

This paragraph introduces the concepts of translational and rotational motion, using a classroom setting with students Bobby and Bo, and teacher Mr. P. Translational motion is explained as the movement of an object's center of mass from one place to another, while rotational motion involves an object moving in circles around its center of mass. The paragraph further discusses how an object can exhibit both types of motion simultaneously. Torque, the rotational force causing angular acceleration, is introduced with its symbol (the lowercase Greek letter tau) and its calculation formula (tau equals r times F times sine theta). The importance of the moment arm or lever arm in calculating torque is highlighted, and examples involving a bicycle wheel and door handles are used to illustrate these concepts.

05:03
🔧 Understanding Torque and Moment Arm

This paragraph delves deeper into the understanding of torque and the moment arm. It starts with a discussion on the ineffectiveness of pushing a door at an angle due to the sine of the angle being less than one, which results in less torque. The concept of the sine curve and its maximum value at 90 degrees is explained. The relationship between the angle theta, the force vector, and the r vector is clarified. The moment arm is defined as the perpendicular distance from the axis of rotation to the line of action of the force, and its equivalence to r times sine theta is established. The units of torque (newton meters) are discussed, distinguishing it from work and energy (measured in joules). The summary ends with a reinforcement of the concepts learned and a thank you note from Mr. P to the students for their active participation.

Mindmap
Keywords
💡Torque
Torque is a measure of the rotational force that can cause an object to rotate around an axis. In the context of the video, it is described as the ability of a force to cause angular acceleration. The concept is illustrated by applying torque to a bicycle wheel to make it spin, demonstrating the rotational motion. Torque is calculated as the product of the force applied, the moment arm (distance from the axis of rotation), and the sine of the angle between the force and the moment arm. The symbol for torque is the lowercase Greek letter tau (τ), and it has both magnitude and direction, making it a vector quantity.
💡Translational Motion
Translational motion refers to the movement of an object from one place to another, where all parts of the object move the same distance and in the same direction. In the video, Bobby explains that translational motion occurs when the center of mass of an object moves from one location to another. This is contrasted with rotational motion, where the object spins around its center of mass.
💡Rotational Motion
Rotational motion is when an object moves in a circular path around a central point, known as the center of mass. In the video, Billy describes rotational motion as the spinning of an object around its center of mass, and it is exemplified by a bicycle wheel turning on its axis.
💡Center of Mass
The center of mass is the point at which the mass of an object, or a system of objects, is concentrated. It is the balance point of the object and is used to describe the motion of the object as a whole. In the video, the center of mass is used to differentiate between translational and rotational motion, with translational motion involving movement of the center of mass and rotational motion occurring around it.
💡Angular Acceleration
Angular acceleration is the rate of change of angular velocity, which is a measure of how quickly an object rotates or spins. In the video, Billy explains that when Mr. P applies torque to the bicycle wheel, he changes its angular velocity, thus causing angular acceleration. This concept is crucial in understanding how torque affects rotational motion.
💡Moment Arm
The moment arm, also known as the lever arm, is the perpendicular distance from the axis of rotation to the line of action of the force applied. It is a critical factor in calculating torque, as it multiplies with the force to produce torque. The moment arm maximizes the effectiveness of the applied force in causing rotation.
💡Sine Theta
In the context of torque, sine theta represents the sine of the angle between the force vector and the moment arm (or lever arm). The sine function is used in the torque equation to determine the component of the force that is effective in causing rotation. The sine of 90 degrees is 1, which means that the force is applied perpendicular to the moment arm, maximizing torque.
💡Vector
A vector is a quantity that has both magnitude and direction. In the video, torque is described as a vector because it has a specific size (magnitude) and a direction in which it acts to cause rotational motion. This is important because it means that torque can be added or subtracted according to the parallelogram rule, just like other vectors.
💡Work and Energy
Work and energy are scalar quantities related to the movement of objects. Work is the measure of energy transferred by a force acting over a distance, while energy is the capacity to do work. Although newton meters (Nm) are used as units for both torque and work/energy, they are fundamentally different. Torque is a vector that causes rotational motion, whereas work and energy are scalars related to linear motion and the capacity to do work.
💡Supplementary Angles
Supplementary angles are two angles whose sum is 180 degrees. The sine of supplementary angles has the same value, which is important in the context of torque calculation when considering the angle between the force vector and the moment arm. This property allows for flexibility in calculating torque, as using either angle results in the same sine value.
💡Joule
A joule is the unit of energy in the International System of Units (SI). It is used to measure work done or energy transferred. While newton meters (Nm) are commonly used as the unit for torque, they are equivalent to joules because torque is the rotational equivalent of force (newtons) applied over a distance (meters). However, to differentiate between torque and work/energy, the unit newton meters is typically used for torque.
Highlights

Torque is the ability of a force to cause angular acceleration.

Torque is represented by the lowercase Greek letter tau (τ).

The formula for torque is τ = r * F * sin(θ), where r is the moment arm, F is the force, and θ is the angle between the force and the moment arm.

The moment arm (r) is the perpendicular distance from the axis of rotation to the point where the force is applied.

The maximum torque is achieved when the angle (θ) between the force and the moment arm is 90 degrees, as sin(90°) = 1.

When the force is applied directly at the axis of rotation, the moment arm is zero, and no torque is produced.

The direction of torque is such that it tends to rotate an object about its axis of rotation.

In the context of doors, pushing near the handle (far from the hinge) creates a larger moment arm and thus greater torque, making it easier to open the door.

Pushing at an angle to the door reduces the moment arm and consequently the torque, making it less effective to open the door.

Pushing perpendicularly to the door (at a 90-degree angle) results in the most efficient torque for opening the door.

The sine function is crucial in calculating torque, as it accounts for the effective component of the force that contributes to rotation.

Torque is a vector quantity, having both magnitude and direction, which is why its unit is newton-meters (Nm), distinct from the unit for work and energy (joules).

The concept of translational and rotational motion is essential for understanding torque, as an object can have both types of motion simultaneously.

The bicycle wheel examples illustrate the differences between translational motion (center of mass moving), rotational motion (wheel spinning), and combined motion.

Applying and removing force to a spinning wheel are demonstrations of applying net torque to cause changes in angular velocity.

Understanding the relationship between the force applied, the moment arm, and the angle can optimize the application of torque in practical scenarios, like opening a door.

The discussion on the r vector and the moment arm provides a deeper understanding of how the position and direction of the applied force influence torque.

Supplementary angles and the sine curve explain why pushing at an angle or directly at the axis of rotation results in less or no torque, respectively.

Transcripts

Browse More Related Video

Torque, Basic Introduction, Lever Arm, Moment of Force, Simple Machines & Mechanical Advantage

torque explained

Rotational version of Newton's second law | Physics | Khan Academy

AP Physics 1 - Torque

AP Physics 1 Torque and Rotational Motion Review

Torque

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEducationTorqueConceptsRotationalMotionTranslationalMotionAngularAccelerationMechanicalPrinciplesBicycleWheelExamplesDoorMechanicsForceApplicationSineCurve