How to solve Rotational Equilibrium Problems
TLDRIn this educational video clip, Dan the Tutor explains the concept of rotational equilibrium in physics, a topic related to torques. He emphasizes that the net torque in a system at rotational equilibrium equals zero, meaning the torques acting in opposite directions are balanced. Using the formula for torque (force times distance), Dan illustrates how to solve problems involving rotational equilibrium by focusing on the forces acting on the bar or lever, rather than the individual masses. He works through two examples: one involving a balance beam with different masses and another more complex scenario with a bar of significant mass and a 10-kilogram box. In the first example, he calculates the position 'x' for balance using torques and in the second, he determines the normal forces on both sides of the bar. Throughout the explanation, Dan highlights the importance of choosing an appropriate pivot point to simplify the problem and emphasizes that in rotational equilibrium, the system does not rotate. He also touches on translational static equilibrium, showing how to calculate the normal forces on both sides of a lever system. The video is aimed at providing a clear understanding of rotational equilibrium and its applications in physics.
Takeaways
- 📚 The concept of rotational equilibrium is introduced as a topic within the study of torques, where the net torque equals zero, indicating a balance between counterclockwise and clockwise torques.
- 🔍 To solve rotational equilibrium problems, one can use the definition of torque (force times the distance from the pivot) along with the condition that the net torque is zero.
- 🤔 In problems where units are given in centimeters, it's acceptable to use them directly or convert to meters, as the choice of units does not affect the solution for rotational static equilibrium problems.
- 📐 When dealing with a balance beam problem, the force due to gravity (mass times gravity) acts on the objects, and the torque is calculated based on the distance from the pivot point.
- 📈 The torques from the two sides of the balance beam are set equal to each other to find the unknown distance (x), using the formula for torque and the given masses and distances.
- 🧐 The direction of the torque (clockwise or counterclockwise) is important, but the sign can be manipulated in the equations to avoid dealing with negatives, as the net torque is zero in equilibrium.
- 🔧 In more complex problems, such as those involving a beam with mass, additional forces like the normal force and the weight of the beam itself must be considered in the torque calculations.
- 🎯 Choosing the pivot point is a strategic decision that can simplify the problem by eliminating one of the unknown variables, often by placing the pivot at a point where the torque due to one of the forces becomes zero.
- 📝 When two unknown variables are present, it's common to use one equation that represents rotational equilibrium and another that represents translational static equilibrium (ΣFy = 0) to solve for both unknowns.
- 🤹♂️ The normal force on each side of a beam can differ, reflecting the distribution of mass and the distances from the pivot point, which is intuitively understood and confirmed by the problem's solution.
- 🌟 The video script provides a step-by-step approach to solving equilibrium problems, emphasizing the importance of understanding the principles of torque and the strategic selection of the pivot point.
Q & A
What is rotational equilibrium in the context of the video?
-Rotational equilibrium refers to a state where the net torque acting on an object is zero, meaning the object is not rotating and is perfectly balanced.
What is the basic equation Dan uses to solve for rotational equilibrium?
-The basic equation used is that the net torque is equal to zero, which means the torques acting counterclockwise are equal to the torques acting clockwise.
Why does Dan mention that the choice of the pivot point is an art?
-The choice of the pivot point is considered an art because it requires creative decision-making to select the point that simplifies the problem and allows for the cancellation of one of the unknown variables, making the problem easier to solve.
What is the significance of treating the mass of an object as a point source at the center of mass?
-Treating the mass as a point source at the center of mass simplifies the calculation of torques because it allows us to consider the entire mass as acting through a single point, making the torque calculations more straightforward.
How does Dan handle the conversion between centimeters and meters in the problem?
-Dan explains that for problems involving rotational static equilibrium, it doesn't matter whether you use centimeters or meters as long as you are consistent throughout the problem. However, in general, meters are preferred in physics.
What is the role of the normal force in the second example problem presented by Dan?
-In the second example, the normal force acts on the bar and is considered because the bar itself has mass and is subject to gravitational force. The normal forces on both sides of the bar are unknown variables that need to be solved for in the problem.
Why does Dan not include the normal force acting on the masses in the first example?
-Dan does not include the normal force acting on the masses in the first example because, for rotational equilibrium problems, the focus is only on the forces acting on the bar itself, not on the individual masses.
How does Dan solve for the normal force on the right side (nr) in the second example?
-Dan solves for nr by choosing the pivot point on the left side of the bar, which eliminates the torque from the left normal force (nl) since it acts at the pivot point. He then sets up an equation balancing the clockwise and counterclockwise torques and solves for nr.
What is the relationship between rotational equilibrium and translational static equilibrium as explained in the video?
-Rotational equilibrium refers to the absence of rotational motion (net torque equals zero), while translational static equilibrium refers to the absence of linear motion (net force in the y-direction equals zero). In the second example, after finding the normal force on the right side, Dan uses the concept of translational static equilibrium to find the normal force on the left side.
Why is the normal force on the left side slightly higher than the normal force on the right side in the second example?
-The normal force on the left side is higher because the 10-kilogram mass, which contributes to the normal force, is closer to the left side of the bar. This results in a greater moment arm and thus a greater normal force on the left compared to the right.
How does Dan manipulate the equation to avoid dealing with negative signs when calculating torques?
-Dan manipulates the equation by adding the clockwise torque to both sides, which eliminates the need for negative signs. This is possible because the net torque is zero in a state of rotational equilibrium.
Outlines
📚 Introduction to Rotational Equilibrium
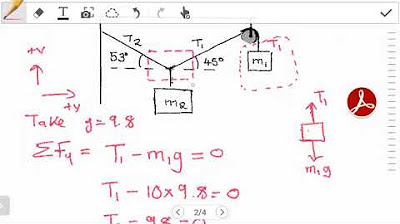
In this first paragraph, Dan the tutor introduces the concept of rotational equilibrium, a topic within the study of torques. He explains that when an object is in rotational equilibrium, the net torque is zero, meaning the torques acting in opposite directions are equal. He uses the definition of torque, which is force times distance, to show how to solve problems in this area. An example is provided involving a balance beam with masses on either side and the calculation to find the position 'x' where the beam is balanced.
🔍 Choosing Units in Static Equilibrium Problems
The second paragraph delves into the specifics of using units like centimeters or meters in static equilibrium problems. Dan clarifies that for such problems, the choice of units does not affect the outcome, as long as they are consistent throughout the calculation. He also discusses the importance of understanding the direction of torques and how to manipulate equations to eliminate the need for negative signs, simplifying the process. A more complex example is then introduced, involving a bar with a mass and forces acting on it.
🎭 Pivot Point Selection in Equilibrium Problems
In the third paragraph, Dan emphasizes the strategic selection of the pivot point in solving equilibrium problems. He illustrates that choosing the pivot point can eliminate one of the unknown variables, simplifying the problem. The paragraph continues with a complex example involving a bar with a mass and a 10-kilogram box, where the forces acting on the bar and the normal forces on either side are considered. Dan shows how to set up the equations and solve for the normal force on the right side of the bar.
🔧 Solving for Normal Forces in a Balanced System
The final paragraph focuses on finding the normal forces on both sides of a system in equilibrium. Dan explains that after finding the normal force on one side, the other can be found using the principle of translational static equilibrium, which considers all forces acting in the vertical direction. He calculates the normal force on the left side and discusses the physical intuition behind why the normal forces on either side of the beam are not equal. The paragraph concludes with a reminder to like and subscribe for more educational content.
Mindmap
Keywords
💡Rotational Equilibrium
💡Torque
💡Pivot Point
💡Normal Force
💡Counterclockwise and Clockwise
💡Fulcrum
💡Centimeters and Meters
💡Mass
💡Gravity
💡Free Body Diagram
Highlights
Rotational equilibrium is defined as a state where the net torque is equal to zero, indicating no rotation.
Torque is calculated as the force applied perpendicular to the axis multiplied by the distance from the axis.
In rotational equilibrium problems, objects are perfectly balanced and do not rotate.
The force acting on objects in the given example is gravity, with mass and gravitational acceleration used in the calculation.
Normal forces are not included in the free body diagram for the bar in rotational equilibrium problems.
The choice of pivot point in solving equilibrium problems can simplify the process by eliminating variables.
For the given balance beam problem, the torques from the masses on either side are calculated based on their distances from the fulcrum.
Units conversion from centimeters to meters is discussed, noting that it's not always necessary in rotational equilibrium problems.
An example problem demonstrates finding the position 'x' where a balance beam is in equilibrium with given masses and distances.
The solution process involves setting up an equation where counterclockwise torques equal clockwise torques.
In a more complex example, the bar itself has mass, and its gravitational force must be considered in the equilibrium calculation.
The pivot point can be chosen arbitrarily, but it's often beneficial to pick a point that simplifies the equation by eliminating a variable.
Translational static equilibrium is introduced as a condition where there is no net force in the vertical direction, leading to no vertical movement.
The normal force on the left side of the beam is found to be slightly higher than on the right due to the closer proximity of the mass to the left.
The process of solving for unknown variables in equilibrium problems is demonstrated through step-by-step algebraic manipulation.
The importance of understanding both rotational and translational equilibrium for solving complex physics problems is emphasized.
The tutor encourages students to practice choosing pivot points and solving equilibrium problems to build problem-solving skills.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: