Finding Local Maxima and Minima by Differentiation

Professor Dave Explains
3 Apr 201806:16
EducationalLearning
32 Likes 10 Comments

TLDRThis script discusses using differentiation to find the maxima and minima of functions. It explains that the derivative gives the slope of the tangent line, which is horizontal at local extrema. By finding where the derivative equals zero, you can locate these points. Examples show finding maxima and minima for polynomials and rational functions. The script also mentions absolute extrema, optimization problems, and how knowing local extrema allows better graph sketching. Overall, it demonstrates applications of differentiation for locating and analyzing extrema of functions.

Takeaways
  • 😀 Differentiation allows us to find maxima and minima of functions
  • 👍 The derivative gives the slope of the tangent line, which is 0 at maxima and minima
  • 📈 To find maxima/minima, take the derivative and find where it equals 0
  • 🔎 Some functions have no maxima/minima, absolute maxima/minima, or local maxima/minima
  • 📉 A function can change direction at maxima and minima points
  • 💡 Use the derivative to find inputs where the tangent line is horizontal
  • 🧮 Set the derivative = 0 and solve to find critical points
  • 😳 The quotient rule can find derivatives of rational functions
  • ☝ Finding zeros of the numerator gives maxima/minima
  • 📊 Adding maxima/minima points improves graphing accuracy
Q & A

  • What is the purpose of finding the maxima and minima of a function?

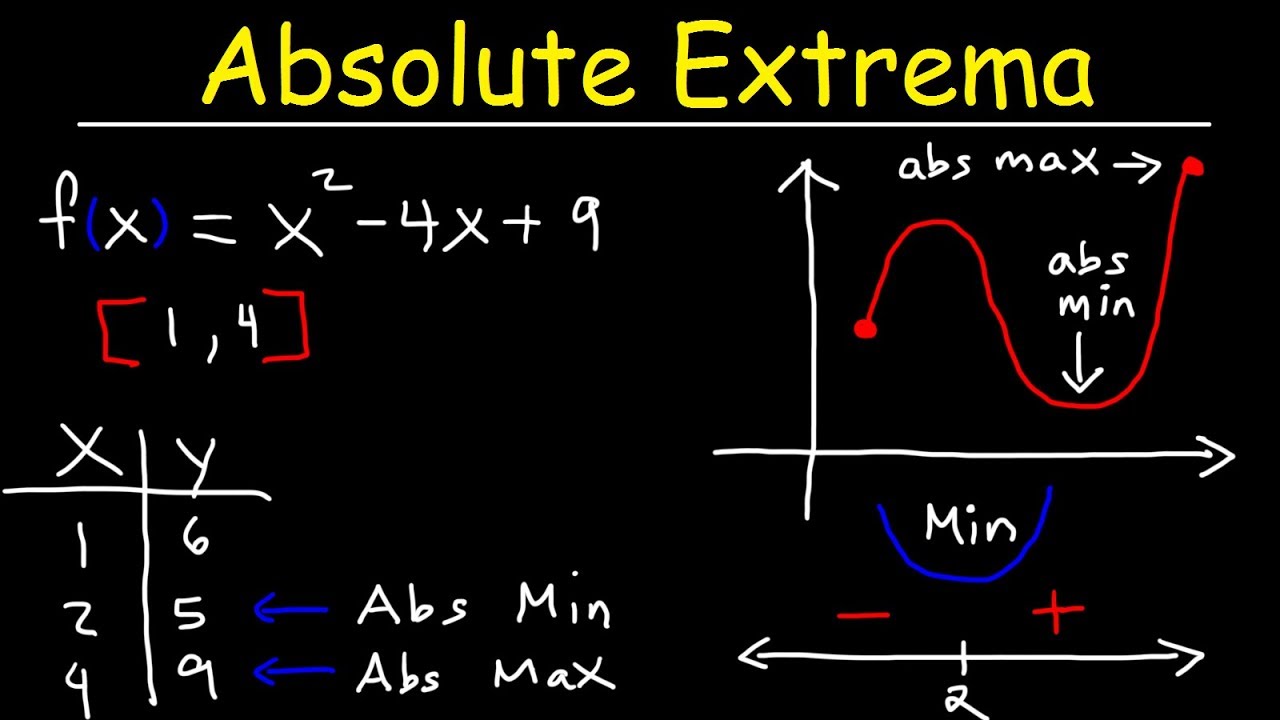
    -Finding the maxima and minima allows us to identify the highest and lowest points on a curve in a particular section. This helps us sketch accurate graphs of functions and solve optimization problems.

  • How do you locate the maxima and minima of a function?

    -You take the derivative of the function, set it equal to 0, and solve for the input values. The inputs that make the derivative 0 will be the locations of any maxima or minima.

  • What type of functions have absolute maxima and minima?

    -Functions like sine and cosine have absolute maxima and minima - these are the highest and lowest values the function can ever reach, regardless of the input.

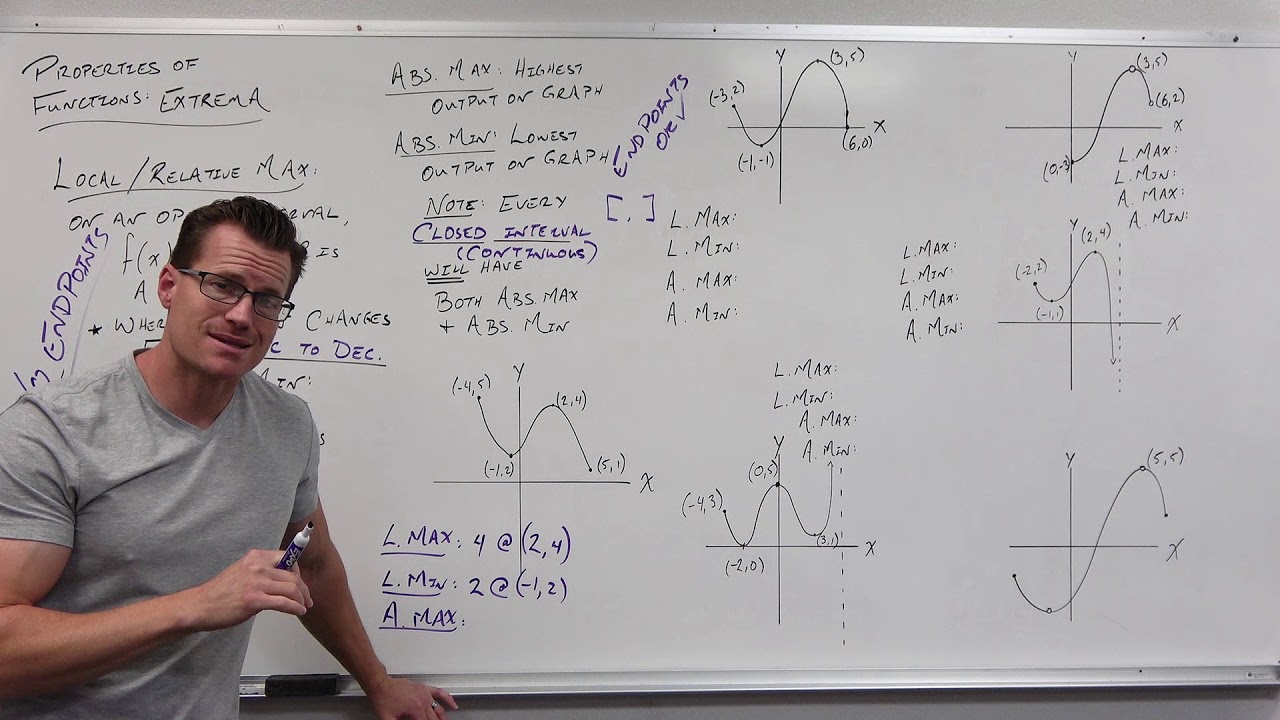
  • What is the difference between a local and an absolute extremum?

    -A local extremum is the highest or lowest point in a particular section of the curve, while an absolute extremum is the highest or lowest value the function ever reaches globally.

  • What polynomial function is analyzed to find maxima and minima?

    -The video analyzes the function f(x) = x^3 - 3x^2 + 1. It has one local maximum at x=0 and one local minimum at x=2.

  • What is the process used to find maxima and minima?

    -1. Take the derivative of the function 2. Set the derivative equal to 0 and solve 3. The inputs that make the derivative 0 are maxima and minima

  • What rule is used to take the derivative of x/(x^2+1)?

    -The quotient rule is used since the function is a rational function - you take the bottom times the derivative of the top, minus the top times the derivative of the bottom, all over the bottom squared.

  • Where are the maxima and minima located for f(x) = x/(x^2+1)?

    -There is a maximum at x=1 and a minimum at x=-1.

  • How do maxima and minima help graph functions?

    -Finding maxima and minima gives additional points on the curve of a function. This allows us to sketch more accurate graphs compared to just using end behavior and zeros.

  • What is an application of finding maxima and minima?

    -Maxima and minima have many applications in optimization problems - finding the optimum cost, profit, area, volume, etc. by locating the extremum points.

Outlines
00:00
😀 Finding Maxima and Minima Using Derivatives

This paragraph introduces the concept of using derivatives to identify maxima and minima of functions. It explains that horizontal tangent lines occur at these points, meaning the derivative is 0. So taking the derivative and finding its zeros reveals where maxima and minima are located. Some examples of functions with and without maxima/minima are shown.

05:01
📈 Revisiting Function Graphing

This paragraph mentions revisiting graphing functions in the context of calculus. It states that finding maxima, minima, and other key points allows drawing better function graphs compared to just using end behavior and zeros. It then says comprehension will be checked.

Mindmap
Keywords
💡Differentiation
Differentiation is the process of finding the derivative of a function. The derivative gives the slope of the tangent line to the function at a given point. Differentiation is a key concept in calculus that is useful for analyzing functions and solving optimization problems.
💡Local maxima and minima
A local maximum is the highest point on a function curve within a neighboring region, while a local minimum is the lowest point on the curve locally. Finding local extrema allows us to understand the shape of a function and critical points in its graph.
💡Horizontal tangent line
At any local maximum or minimum of a function, the tangent line will be horizontal, meaning it has a slope of 0. This property allows us to find maxima and minima by taking the derivative of a function and finding where it equals 0.
💡Absolute maxima and minima
Absolute maximum and minimum refer to the globally highest and lowest values of a function. For example, sine x has an absolute maximum of 1 and minimum of -1, as it never exceeds these bounds.
💡Quotient rule
The quotient rule for differentiation states: Given f(x)=g(x)/h(x), f'(x) = (h(x)·g'(x) - g(x)·h'(x))/h(x)^2. We apply this when differentiating rational functions to find critical points.
💡Higher-degree polynomials
Polynomial functions with degrees greater than 2 can have more complex and non-intuitive graphs. By finding local extrema through differentiation, we can sketch graphs of high-degree polynomials more accurately.
💡End behavior
A polynomial's end behavior refers to the trend its graph exhibits as x approaches positive or negative infinity. Knowing a polynomial's leading term tells us its end behavior, but finding local extrema gives more detail.
💡Critical points
The critical points or stationary points of a function are local maxima, local minima, and points of inflection. Differentiating reveals where the slope is 0, which locates these points that characterize the function's graph.
💡Optimization problems
Many applied problems involve optimizing or maximizing/minimizing some quantity. By finding local extrema, differentiation allows us to optimize functions and solve these types of problems.
💡Applications of differentiation
As illustrated in this video, differentiation and finding derivatives have many practical applications - analyzing functions, graphing, optimization, rates of change, etc. The power of calculus lies in how it can model real-world phenomena.
Highlights

Differentiation allows us to find maxima and minima of functions

At maxima and minima, the derivative of the function equals zero

Finding maxima and minima allows us to optimize problems later on

Some functions have no maxima or minima

Some functions have absolute maxima and minima

Local or relative maxima and minima are the highest or lowest points in a section

To find maxima and minima, take the derivative and find where it equals zero

Maxima and minima give additional points to sketch functions more accurately

The quotient rule can be used to find derivatives of rational functions

Set the numerator equal to zero to find maxima and minima

Maxima and minima allow better graphing of higher degree polynomials

Horizontal tangent lines occur at maxima and minima

Some functions like x^3 have a finite number of local maxima/minima

Derivative gives slope of tangent line, which is zero at maxima/minima

Need to find inputs where derivative equals zero to locate maxima/minima

Transcripts

Browse More Related Video

Relative Extrema

Finding Absolute Maximum and Minimum Values - Absolute Extrema

Finding Relative Extrema

Calculus AB Homework 4.4: Relative Extrema

Properties of Functions - Extrema (Precalculus - College Algebra 10)

Second Derivative Test Multivariable (Calculus 3)

Rate This

5.0 / 5 (0 votes)

Thanks for rating: