Calculating Volume by Cylindrical Shells
TLDRThe script explains and demonstrates the method of cylindrical shells for calculating the volume of a solid of revolution. It starts by deriving the formula for the volume of a hollow cylinder and then shows how this can be adapted to find the volume of a solid of revolution by treating it as made up of many cylindrical shells. The key advantage of this method over previous techniques is that it avoids having to rewrite functions in terms of the axis of rotation. An example applying the cylindrical shell method to find the volume when rotating the region between y=2x^2-x^3 and the x-axis around the y-axis is explained step-by-step.
Takeaways
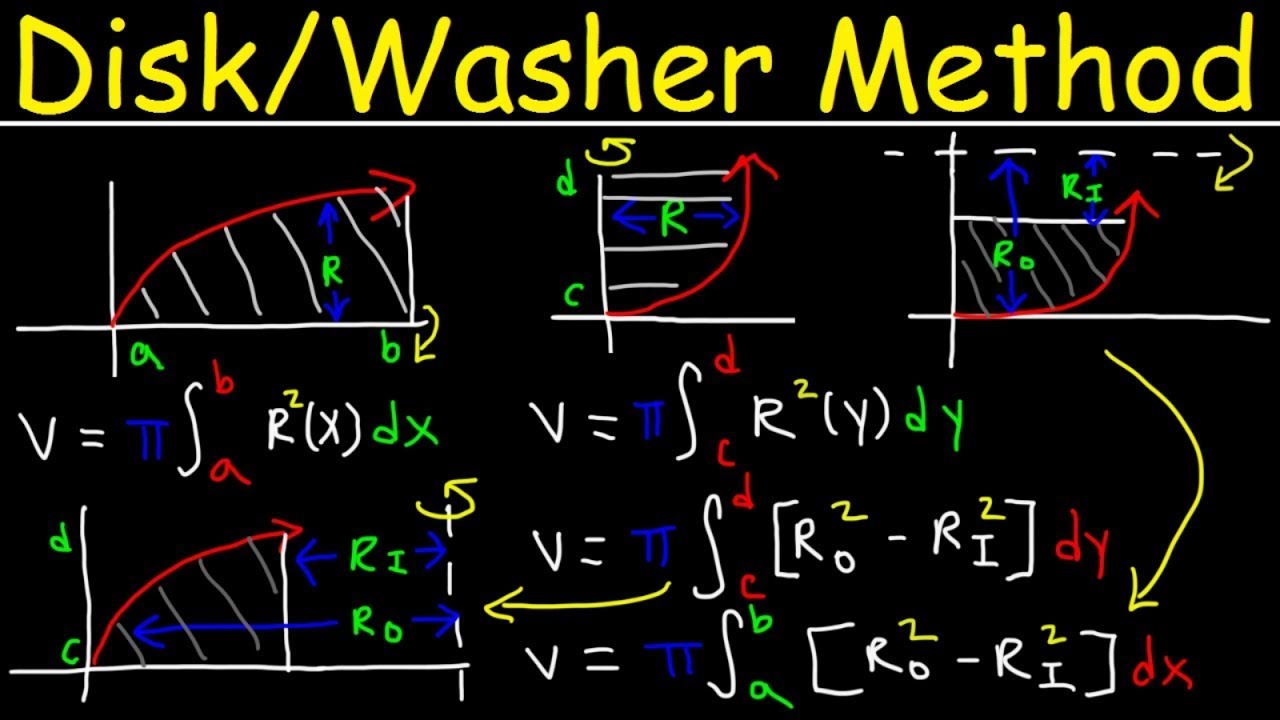
- 😀 The method of cylindrical shells is an alternative to the disk/washer method for computing volumes of revolution.
- 😮💨 The cylindrical shell method can be easier when solving the function for one of the radii is complex.
- 📏 The volume formula for a cylindrical shell is 2πrhΔr, where r is the average radius, h is the height, and Δr is the thickness.
- 😎 To use cylindrical shells, integrate 2πx*f(x) dx over the interval that spans the solid of revolution.
- 👀 Imagine wrapping the region around the axis of rotation to visualize the cylindrical shells.
- 🤓 The disk/washer method integrates cross sections perpendicular to the axis of rotation.
- 😉 Cylindrical shells integrate parallel to the axis of rotation.
- 🧐 Choose disk/washer vs cylindrical shell method based on which integrals are easier to set up.
- 🤔 The cylindrical shell method avoids solving the function for one of the radii.
- ☑️ For practice, apply both methods and compare the complexity of the integral setup.
Q & A
What is the method of cylindrical shells and when is it useful?
-The method of cylindrical shells is a technique to calculate the volume of a solid of revolution when it is difficult to directly calculate the area of cross sections. It involves modeling thin cylindrical slices of the solid and summing their volumes.
What is the formula used to calculate the volume of a cylindrical shell?
-The formula is: Volume = 2πrhΔr, where r is the average radius of the cylindrical shell, h is the height of the cylindrical shell, and Δr is the thickness of the shell.
Why was the washer method difficult to apply in this example?
-The washer method was difficult here because both the inner and outer radii of the washers depend on the same complex function. Solving this function for x in terms of y to integrate was not appealing.
What are the key parameters needed to evaluate the cylindrical shells method?
-The key parameters are: 1) the function f(x) that defines the height, 2) limits of integration spanning the solid, and 3) an expression for 2πx which is the circumference of each shell.
How do you determine the height and radius for each cylindrical shell?
-The height of each shell is given by the function f(x). The radius is simply the variable x, representing the horizontal distance from the axis of revolution.
What is the significance of 2πx in the integral?
-2πx calculates the circumference of each cylindrical shell. When multiplied by the height and thickness, it gives the lateral surface area of each shell.
What are the limits of integration in the final integral?
-The limits of integration span from 0 to 2, because the maximum value of the function f(x) = 2x^2 - x^3 is 2.
What is the advantage of the cylindrical shells method over washers or disks?
-The main advantage is avoiding having to rewrite the function(s) in terms of the radius/radii of the cross sections, which can be algebraically difficult.
For what types of solids would washers/disks be preferred over shells?
-Washers/disks tend to be easier when the function(s) allow the radii of the cross sections to be easily written in terms of the axis of revolution.
How can you decide which method to use for a given solid of revolution problem?
-Analyze the function(s) defining the solid and determine whether it is simplest to directly integrate cross sectional areas or model the solid with cylindrical shells.
Outlines
😐 Deriving the formula for volumes of cylindrical shells
This paragraph derives the formula for calculating the volume of a hollow cylindrical shell using the inner and outer radii. It shows that the volume can be expressed as 2πrΔr, where r is the average radius and Δr is the thickness. This allows calculating volumes without having to rewrite functions in terms of y.
😀 Applying cylindrical shells method to calculate volume
This paragraph applies the cylindrical shells method to calculate the volume of the solid of revolution formed by rotating the region between y=2x^2-x^3 and the x-axis about the y-axis. It shows this method avoids rewriting the function and is easier than the washer method used previously. It also provides some practice problems using this new method.
Mindmap
Keywords
💡solid of revolution
💡disk method
💡washer method
💡cylindrical shells
💡average radius
💡circumference
💡interval of integration
💡cross section
💡function substitution
💡simplifying assumptions
Highlights
Sometimes it won’t be so easy to use the disk/washer method, so let’s look at an example where another method will be a better approach.
The problem is that solving this function for x in terms of y is not a very appealing task.
This is the method of cylindrical shells.
To get the volume of this figure, we calculate the volume of the outer cylinder and subtract the volume of the inner cylinder.
The formula for the volume of a cylindrical shell is 2πrhΔr.
We no longer have to solve for x in terms of y.
The height of the shell is f(x) and the circumference is 2πx.
The volume is the integral of 2πx times f(x) dx over the interval spanning the solid.
For this example, the cylindrical shell method was easier than the washer method.
For any solid of revolution, think critically to figure out which method is best.
It depends on whether it's easy to express the radii with the given functions or if another way is easier.
The cylindrical shell is oriented vertically.
The volume equals the integral of 2πx times f(x) dx over the interval spanning the solid.
You have to figure out if it's easier to find the radii of the cross-section or express things another way.
Let's practice this new cylindrical shell method.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: