AP Physics 1 Torque and Rotational Motion Review
TLDRThis video script offers a comprehensive review of torque and rotational motion in the context of AP Physics 1. It explains the concept of torque, which causes an object to rotate around an axis, and differentiates it from linear force. The script delves into the mathematical relationship between torque, force, and the distance from the axis of rotation, highlighting the importance of the perpendicular component of force for generating torque. It also covers the principles of angular momentum, rotational kinetic energy, and the conservation of angular momentum, emphasizing the impact of an object's mass distribution on its rotational inertia and ease of rotation. The video uses practical examples, such as rolling objects and inclined planes, to illustrate these concepts, reinforcing the understanding of rotational dynamics.
Takeaways
- 🌀 Torque is the rotational equivalent of force, causing an object to rotate around an axis within the object.
- 📐 The equation for torque is τ = r * F, where r is the distance from the axis of rotation and F is the force applied.
- 🔽 The torque is maximized when the force is applied perpendicular to the lever arm (moment arm).
- 📊 The true torque equation is τ = r * F * sin(θ), accounting for the angle between the force and the lever arm.
- 🔄 Objects with mass distributed closer to the axis of rotation have less moment of inertia and rotate more easily.
- 🏎️ In problems of rotational motion, the moment of inertia (I) and angular acceleration (α) are related by the net torque (τ), as in τ = I * α.
- 📉 The conservation of angular momentum occurs when the net external torque on a system is zero.
- 🌪️ Angular momentum is given by L = I * Ω and is conserved when there is no net external torque, similar to linear momentum conservation.
- 🚀 The inclined plane demonstration shows that a block of ice (translational motion) will reach the bottom before a rolling sphere (rotational motion) due to energy distribution.
- 🔄 The direction of torque (clockwise or counterclockwise) is determined by the position of the force application relative to the axis of rotation.
- 📚 The video script serves as a comprehensive review of rotational motion concepts, including torque, moment of inertia, angular momentum, and their relationships with linear quantities.
Q & A
What is the primary difference between translational motion and rotational motion?
-Translational motion involves an object moving from one position to another, whereas rotational motion involves an object spinning or revolving around an axis of rotation.
What is torque and how is it related to force?
-Torque is a measure of the force's tendency to cause an object to rotate around an axis. It is related to force as it is the product of the force applied and the distance from the axis of rotation (moment arm).
What is the correct equation for torque?
-The correct equation for torque is tau (τ) equals the product of the force (F), the distance from the axis of rotation (R), and the sine of the angle (θ) between the force vector and the lever arm, written as τ = F * R * sin(θ).
What is the significance of the moment arm in calculating torque?
-The moment arm, which is the distance from the axis of rotation to the point where the force is applied, is significant because it determines the effectiveness of the force in creating torque. A longer moment arm results in a greater torque for the same amount of force.
How does the orientation of the force relative to the lever arm affect the torque?
-The torque is maximum when the force is applied perpendicular to the lever arm. If the force is parallel to the lever arm, it does not create any torque, as the sine of 0 or 180 degrees is zero.
What is the relationship between torque and angular acceleration?
-According to Newton's second law for rotation, the net torque (τ) is equal to the moment of inertia (I) times the angular acceleration (α), expressed as τ = I * α. This means that a larger torque results in a greater angular acceleration for an object with a given moment of inertia.
What is the role of the moment of inertia in rotational motion?
-The moment of inertia (I) is a measure of an object's resistance to rotational motion. It depends on the mass distribution relative to the axis of rotation and affects how easily an object can be set into rotation.
How does the distribution of mass affect the moment of inertia of an object?
-The moment of inertia is directly related to how mass is distributed in an object. Objects with mass distributed closer to the axis of rotation have a smaller moment of inertia and thus rotate more easily compared to those with mass distributed further away from the axis.
What is the relationship between linear and angular quantities?
-Linear and angular quantities are related but deal with different types of motion. Linear quantities (like force, velocity, and acceleration) are used for translational motion, while angular quantities (like torque, angular speed, and angular acceleration) are used for rotational motion. They can be converted into each other using appropriate factors like the radius of rotation.
How is the conservation of angular momentum demonstrated in real-life scenarios?
-The conservation of angular momentum can be observed when an ice skater spins. When the skater pulls their arms in, their moment of inertia decreases and their angular speed increases, conserving the angular momentum. Similarly, when they extend their arms, their moment of inertia increases and their angular speed decreases, again conserving angular momentum.
What is the difference between linear impulse and angular impulse?
-Linear impulse is the change in linear momentum due to an external force acting over a time interval, while angular impulse is the change in angular momentum due to an external torque acting over a time interval. Both are related through the principles of conservation of momentum and impulse, but they apply to different types of motion (linear vs. angular).
Outlines
📚 Introduction to Torque and Rotational Motion
This paragraph introduces the concept of torque and rotational motion in the context of AP Physics 1. It explains how forces can cause translational motion, moving an object from point A to point B, and contrasts this with rotational motion, where an object revolves around an axis within the object. The definition of torque is given, relating it to the force applied and the distance from the axis of rotation (R). The importance of the axis of rotation in understanding rotational motion problems is emphasized, and the generic equation for torque (tau = R * F) is introduced, highlighting the units of Newton meters.
📐 The Torque Equation and its Implications
The paragraph delves deeper into the torque equation, explaining that it is more complex than initially presented. The true equation is torque = R * F * sine(theta), where theta is the angle between the force and the lever arm (moment arm). The lever arm is the distance from the axis of rotation to the point where the force is applied. The paragraph clarifies that only forces perpendicular to the lever arm can generate torque, and it introduces the concept of the sine component, which is crucial when the force is applied at an angle. The distinction between the parallel and perpendicular components of a force is discussed, emphasizing that only the perpendicular component contributes to torque.
🔄 Balanced and Unbalanced Torques
This section discusses the concepts of balanced and unbalanced torques. It explains that if there are balanced torques acting on an object, the net torque is zero, and the object remains at rest or continues to rotate at a constant speed. The paragraph uses the example of a rod with forces applied at different points to illustrate how torques can balance out. Conversely, unbalanced torques result in angular acceleration of the object, as explained by Newton's second law for rotation. The relationship between net torque, moment of inertia, and angular acceleration is highlighted, emphasizing the impact of torque on an object's rotational motion.
🌐 Rotational Kinematics and Moment of Inertia
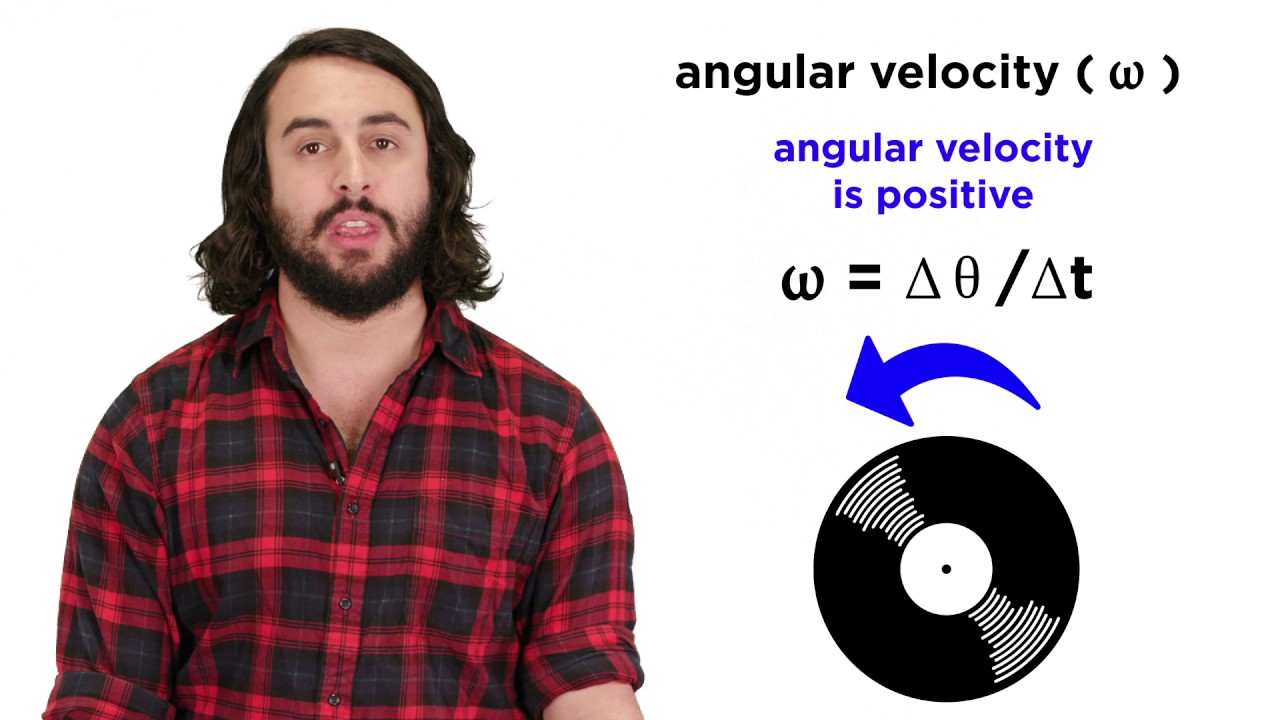
The paragraph covers rotational kinematics, redefining quantities from linear kinematics for rotational scenarios. It introduces the concepts of angular displacement (Delta Theta), angular speed, and angular acceleration. The rotational kinematic equations are presented, drawing parallels with their linear counterparts. The paragraph also touches on the importance of understanding the moment of inertia (I), which is analogous to mass in rotational dynamics, and its role in determining how easily an object rotates. The concept of work in the context of rotational motion is briefly mentioned, contrasting it with torque.
🏎️ Moment of Inertia and Its Effects on Rotation
This section focuses on the moment of inertia, explaining its significance in determining the ease with which an object rotates. It states that objects with mass distributed closer to the axis of rotation will rotate more easily. The moment of inertia is described as a quantity that depends on the mass distribution of the object and its axis of rotation. The paragraph provides examples of different objects (like a disc, hoop, and rod) and their respective moments of inertia, illustrating how the distribution of mass affects the ease of rotation. The concept is reinforced with a real-world example of rotating long rods with different mass distributions.
💫 Rotational Kinetic Energy and Angular Momentum
The paragraph introduces rotational kinetic energy, which is different from translational kinetic energy, and provides the equation for calculating it. It explains the concept of angular momentum, drawing parallels with linear momentum, and describes it as the product of the moment of inertia and angular speed. The conservation of angular momentum is discussed, stating that it is conserved when the net external torque on a system is zero. The paragraph also touches on the concept of angular impulse, which is related to changes in angular momentum due to external torques.
🔄 Directionality in Rotational Motion
This section addresses the concept of directionality in rotational motion, explaining that while linear quantities have positive or negative directions, rotational quantities are described as clockwise or counterclockwise. It emphasizes the importance of considering the axis of rotation when determining the direction of torque. The paragraph concludes with a discussion on how to determine whether a torque is positive or negative based on the direction of rotation it causes, highlighting that the force's effect on rotation depends on its application point relative to the axis of rotation.
Mindmap
Keywords
💡Torque
💡Rotational Motion
💡Axis of Rotation
💡Moment Arm
💡Moment of Inertia
💡Angular Acceleration
💡Angular Velocity
💡Rotational Kinetic Energy
💡Angular Momentum
💡Conservation of Energy
Highlights
Torque is a quantity similar to force but causes an object to rotate around an axis within the object.
The generic equation for torque uses the Greek symbol tau (τ) and is equal to R times F, where R is the distance from the force application to the axis of rotation and F is the force.
Torque's true equation is τ = R * F * sine(theta), accounting for the angle between the force and the lever arm.
Only forces perpendicular to the lever arm can generate torque, while parallel forces do not.
The moment of inertia is a measure of an object's resistance to rotational motion and depends on the mass distribution relative to the axis of rotation.
Objects with mass distributed closer to the axis of rotation have less moment of inertia and rotate more easily.
The conservation of angular momentum is observed when the net external torque on a system is zero.
Angular momentum is defined as L = I * Omega and has units of kilograms meters squared per second.
Angular impulse is related to the change in angular momentum due to an external torque and is given by L_F - L_I = torque * time interval.
Rotational kinetic energy is given by K_rot = 0.5 * I * Omega^2 and is measured in joules, similar to translational kinetic energy.
The inclined plane demonstration shows that a solid sphere rolling without slipping reaches the bottom later than a block of ice sliding without friction due to the energy distribution between translation and rotation.
For rotational motion, directions are described as clockwise or counterclockwise instead of positive or negative.
The moment of inertia varies depending on the object's mass distribution and the axis of rotation chosen.
Torque can be calculated by finding the perpendicular component of the force to the lever arm when the force is applied at an angle.
In static equilibrium, both the net force and the net torque on an object must be zero for the object to remain at rest.
The rotational kinematic equations are analogous to their translational counterparts, with rotational quantities replacing linear ones.
The conservation of energy principle applies to both translational and rotational motion, with potential, kinetic, and other forms of energy considered.
Linear impulse is related to the change in linear momentum and is given by ΔP = (P_F - P_I) = average force * time interval.
Transcripts
Browse More Related Video

2022 Live Review 7 | AP Physics 1 | Understanding Torque and Rotational Motion

2022 Live Review 6 | AP Physics C: Mechanics | Rotational Dynamics and Angular Momentum

College Physics 1: Lecture 25 - Moment of Inertia and Rotational Dynamics
Angular Motion and Torque
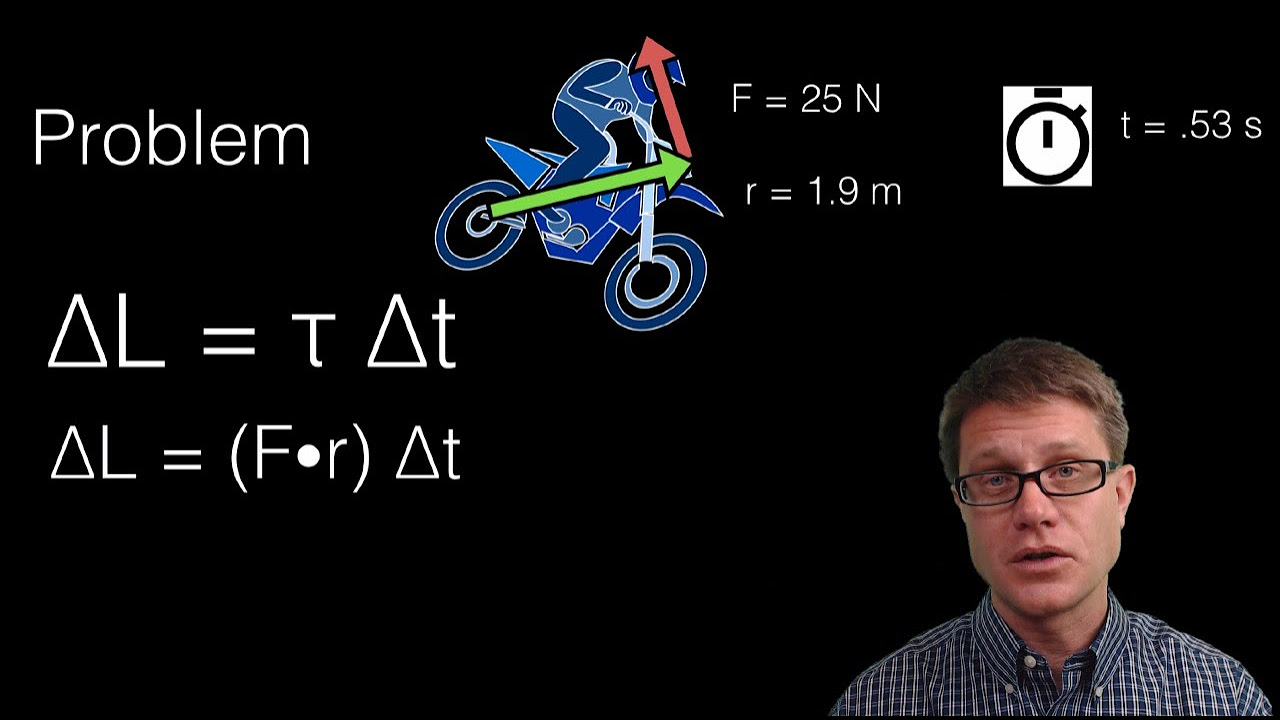
Angular Impulse

AP Physics 1: Rotational Dynamics Review
5.0 / 5 (0 votes)
Thanks for rating: