AP Physics Workbook 1.H Relationship between Position,Velocity and Acceleration

Mr.S ClassRoom
2 Apr 202014:35
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the relationship between position, velocity, and acceleration in physics, using the example of a car's motion. It explains how to derive the velocity equation from a velocity-time graph, highlighting that the slope of the graph represents acceleration. The video also addresses a common misconception about the car's motion, clarifying that the car slows down initially and then speeds up in the opposite direction. The constant acceleration of the car is emphasized, and a position-time graph is sketched to illustrate the car's motion. The concepts are explained with a focus on visual understanding and practical application of physics principles.

Takeaways
  • πŸ“ˆ The relationship between position, velocity, and acceleration is central to understanding the motion of the car.
  • πŸš— The car starts at position zero (X = 0) with a given velocity.
  • ⏱️ Time is the input in seconds, and velocity is the output.
  • πŸ“Š The velocity versus time graph is modeled with the equation y = mx + b, where y is velocity and x is time.
  • πŸ”„ The slope of the velocity-time graph represents acceleration, defined as the change in velocity (Ξ”v) over the change in time (Ξ”t).
  • πŸ…ΏοΈ The y-intercept of the velocity-time graph indicates the initial velocity of the car, which is 12 meters per second in this case.
  • πŸ”’ A general equation for the motion of the cart is derived using standard physics symbols: V = u + at, where V is velocity, u is initial velocity, a is acceleration, and t is time.
  • πŸ”„ The car's motion changes from slowing down in the positive direction to speeding up in the negative direction at around 3 seconds.
  • 🏁 The horizontal intercept of the velocity-time graph represents the time when the car's velocity is zero, indicating a stop.
  • πŸ“‰ The constant slope of the line in the velocity-time graph indicates a constant acceleration of 4 m/sΒ².
  • πŸ“ˆ The position versus time graph can be inferred from the velocity-time graph, showing the car's movement over time, with the graph curving to reflect the changing velocity.
Q & A

  • What is the relationship between position, velocity, and acceleration as described in the transcript?

    -The relationship between position, velocity, and acceleration is described using the equation of motion for a car starting at position zero. The velocity versus time graph is modeled using the equation y = mx + b, where the slope (m) represents acceleration and the y-intercept (b) represents the initial velocity.

  • How is the input and output defined in the context of the velocity versus time graph?

    -In the context of the velocity versus time graph, the input is time (in seconds) and the output is velocity. The graph shows how velocity changes with respect to time.

  • What is the slope of the velocity versus time graph as described in the script?

    -The slope of the velocity versus time graph is calculated as the change in velocity (Ξ”y) over the change in time (Ξ”x). In the script, Ξ”y is 16 and Ξ”x is 4, resulting in a slope of -4/1 or -4 m/s.

  • What is the general equation for the motion of the cart using standard physics symbols?

    -The general equation for the motion of the cart is given by vx = ax * t + vx0, where vx is the velocity in the x-direction, ax is the acceleration in the x-direction, t is time, and vx0 is the initial velocity in the x-direction.

  • How does the car's motion change at 3 seconds according to the script?

    -At 3 seconds, the car's motion changes from traveling in the positive direction to traveling in the negative direction. This is inferred from the velocity versus time graph, where the velocity crosses zero, indicating the car momentarily stops before changing direction.

  • What is the constant acceleration of the car as described in the script?

    -The constant acceleration of the car is described as -4 m/s^2. This is derived from the slope of the velocity versus time graph, which remains constant throughout the motion.

  • How can the position versus time graph be interpreted based on the given information?

    -The position versus time graph can be interpreted by considering the slope of the velocity versus time graph. The graph should start slow, then increase in speed, and finally slow down again as the velocity decreases from an initial positive value, crosses zero, and becomes negative.

  • What is the significance of the horizontal line in the velocity versus time graph?

    -The horizontal line in the velocity versus time graph represents the time when the car's velocity is equal to zero. This is the point where the car momentarily stops before changing its direction of motion.

  • How does the shape of the velocity versus time graph affect the position versus time graph?

    -The shape of the velocity versus time graph directly influences the position versus time graph. If the velocity graph is concave down, the position graph will start with a slow increase, then a faster increase, and finally a slower increase as the velocity decreases. The position graph's shape mirrors the velocity graph's rate of change.

  • What is the initial velocity of the car according to the script?

    -The initial velocity of the car, as indicated by the y-intercept on the velocity versus time graph, is 12 meters per second.

  • How does the acceleration graph (a vs. t) look like based on the information in the script?

    -The acceleration graph (a vs. t) would be a horizontal line because the acceleration is constant at -4 m/s^2 throughout the motion. This constant acceleration indicates that the car's velocity changes at a steady rate over time.

Outlines
00:00
πŸ“š Introduction to Physics Concepts

This paragraph introduces the AP Physics workbook and discusses the relationship between position, velocity, and acceleration. It uses the example of a car's motion, starting from position zero, and explains how this motion is modeled in a velocity versus time graph. The key concept explained here is the equation y = mx + b, where 'm' represents the slope (acceleration) and 'b' is the y-intercept (initial velocity). The paragraph also illustrates how to derive the general equation for the motion of the cart using standard physics symbols and emphasizes the importance of understanding the slope's meaning in terms of acceleration.

05:03
πŸš— Analysis of Car's Motion and Acceleration

In this paragraph, the analysis of the car's motion is continued, focusing on the car's velocity changes over time. It is explained that the car initially slows down, as its velocity decreases from 12 meters per second to 0, and then it speeds up in the opposite direction, with the velocity reaching -4 meters per second. The paragraph clarifies that the car's acceleration remains constant at 4 meters per second squared, as indicated by the unchanging slope of the velocity-time graph. The horizontal intercept on the graph represents the time when the car's velocity is zero, signifying a brief stop before the car starts moving in the opposite direction.

10:06
πŸ“ˆ Graphing Acceleration and Position

The final paragraph discusses the process of graphing the car's acceleration and position over time. It emphasizes that the acceleration is constant and should be represented by a flat line in the graph. The paragraph also explores two possible interpretations of the position-time graph, describing the shape and slope of the graph in both scenarios. The key takeaway is understanding the relationship between the slope of the velocity-time graph and the shape of the position-time graph, as well as the significance of the car's velocity being positive or negative in relation to its direction of motion.

Mindmap
Keywords
πŸ’‘Position
In the context of the video, position refers to the location of the car along a given axis, starting from an initial point, which is considered as position zero (X = 0). It is a fundamental concept in physics to describe the motion of an object. The video uses the position versus time graph to illustrate the car's movement, showing how the car's position changes over time.
πŸ’‘Velocity
Velocity is a physical quantity that describes the rate of change of an object's position with respect to time. It is a vector quantity, meaning it has both magnitude and direction. In the video, the velocity of the car is given in meters per second (m/s), and the velocity versus time graph is used to analyze the car's motion, showing how the car's speed changes over time.
πŸ’‘Acceleration
Acceleration is the rate of change of velocity with respect to time. It quantifies how quickly an object's velocity changes. In the video, the constant acceleration of the car is discussed, with a magnitude of -4 m/sΒ², indicating that the car is decelerating at a constant rate. The negative sign denotes that the acceleration is in the opposite direction to the initial positive velocity.
πŸ’‘Slope
The slope in the context of the video refers to the gradient of the line in the velocity versus time graph. It represents the change in velocity (Ξ”V) over the change in time (Ξ”T), which is essentially the acceleration of the car. A negative slope indicates that the velocity is decreasing over time.
πŸ’‘Graph
A graph is a visual representation of data or mathematical functions. In the video, graphs are used to illustrate the car's motion, with the position versus time graph and the velocity versus time graph being the primary tools to analyze the car's behavior. Graphs help in visualizing the relationships between different physical quantities.
πŸ’‘Time
Time is a fundamental physical quantity that refers to the progression of events. In the video, time is measured in seconds and is used as the independent variable in the graphs to analyze the car's motion. It is the 'x' axis in the position versus time graph and the 'x' axis in the velocity versus time graph.
πŸ’‘Delta (Ξ”)
Delta (Ξ”) is used in mathematics and physics to represent a change or difference in a quantity. In the video, Ξ”Y represents the change in velocity (Ξ”V), and Ξ”X represents the change in time (Ξ”T). These differences are used to calculate the slope, which in turn is used to determine the acceleration of the car.
πŸ’‘Direction
Direction refers to the path or way in which something moves or is oriented. In the video, the direction of the car's velocity is indicated by the sign (positive or negative) of the velocity value. Positive values indicate motion in one direction along the axis, while negative values indicate motion in the opposite direction.
πŸ’‘Intercept
In the context of the video, the intercept refers to the point where the graph of the velocity versus time or position versus time intersects with the axis. For the velocity versus time graph, the y-intercept represents the initial velocity of the car. The intercept is a key feature when analyzing linear relationships in graphs.
πŸ’‘Physics
Physics is the natural science that studies matter, its motion, and the forces that act on it. The video is a physics workbook and discusses concepts such as position, velocity, acceleration, and their relationships, which are all fundamental to understanding the motion of objects in physics.
πŸ’‘Equation
An equation in the context of the video refers to a mathematical statement that expresses the relationship between different physical quantities. The video derives equations to model the car's motion based on the data provided in the velocity versus time graph.
Highlights

The relationship between position, velocity, and acceleration is discussed.

The motion of a car is modeled using a velocity versus time graph.

The equation y equals mx plus b is used to determine the velocity versus time graph.

The input for the model is time in seconds, and the output is velocity.

The slope of the velocity versus time graph represents acceleration.

The y-intercept of the velocity graph indicates the initial velocity of the car.

A general equation for the motion of the cart is derived using standard physics symbols.

The car's motion is analyzed, showing it starts with an initial velocity of 12 m/s.

The car's velocity decreases for the first three seconds and then increases for the last second.

The car's acceleration is constant at -4 m/s^2, as indicated by the unchanging slope of the line.

The horizontal intercept of the velocity graph shows the time when the car's velocity is zero.

The position versus time graph for the car's motion is discussed with two possible interpretations.

The position graph should start slow, then speed up, and finally slow down again.

The velocity graph should be linear, and the acceleration graph should be flat.

The car's motion changes from positive to negative direction at around 3 seconds.

The car stops at exactly 3 seconds when its velocity reaches zero.

The car's acceleration remains constant throughout its motion.

Transcripts

Browse More Related Video

AP Physics Workbook 1.G Graphs of Velocity

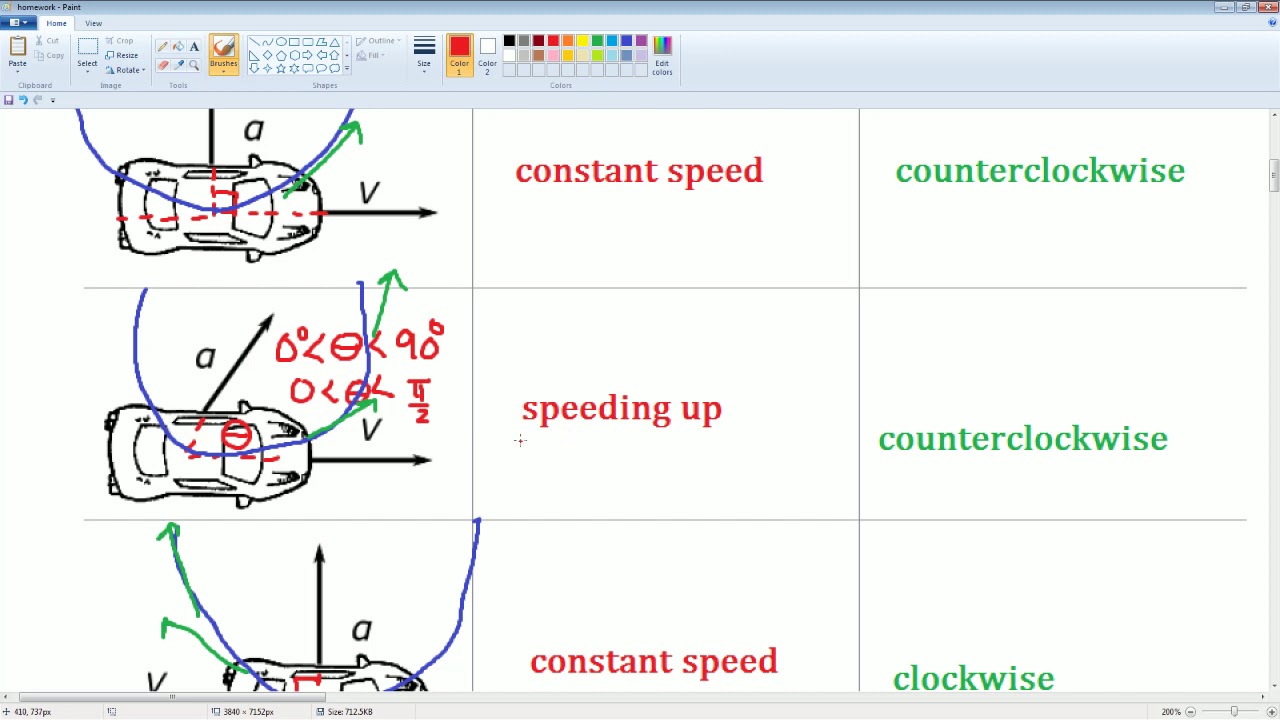
AP Physics Workbook 3.B Direction of Acceleration and Velocity

Motion Diagram for an Accelerating Car | Physics with Professor Matt Anderson | M2-02

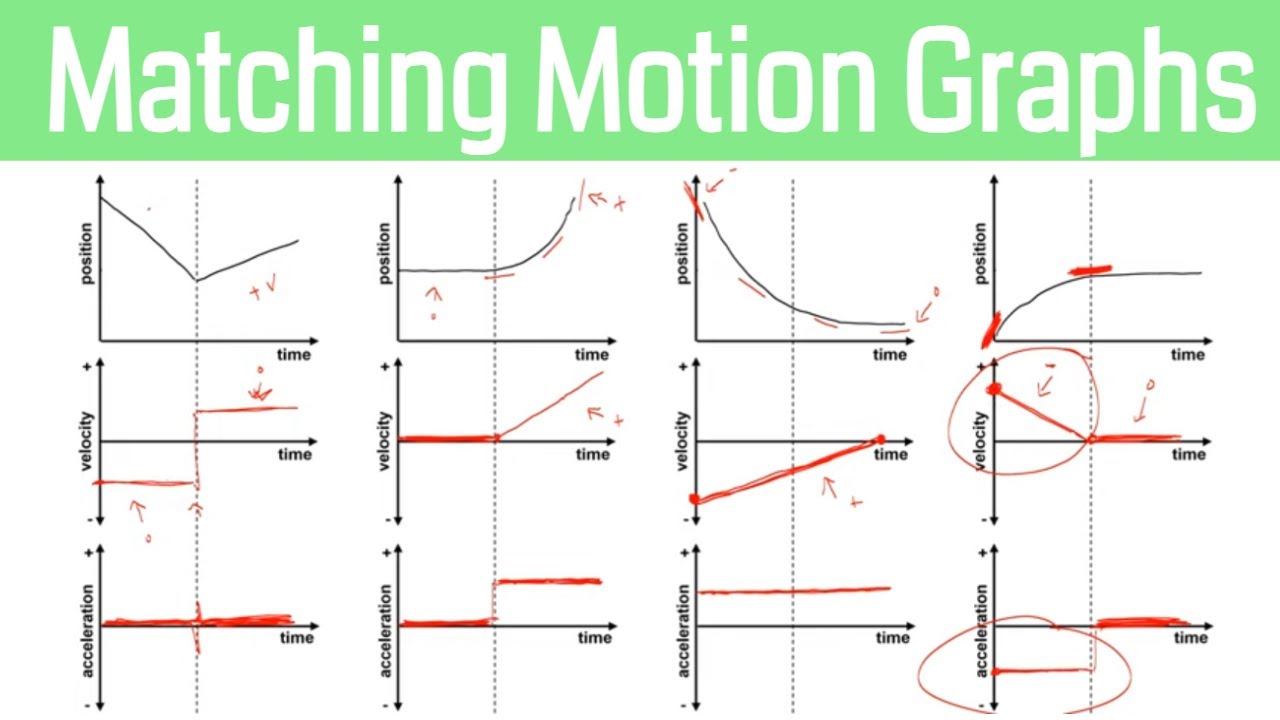
How to Match Motion Graphs in Physics

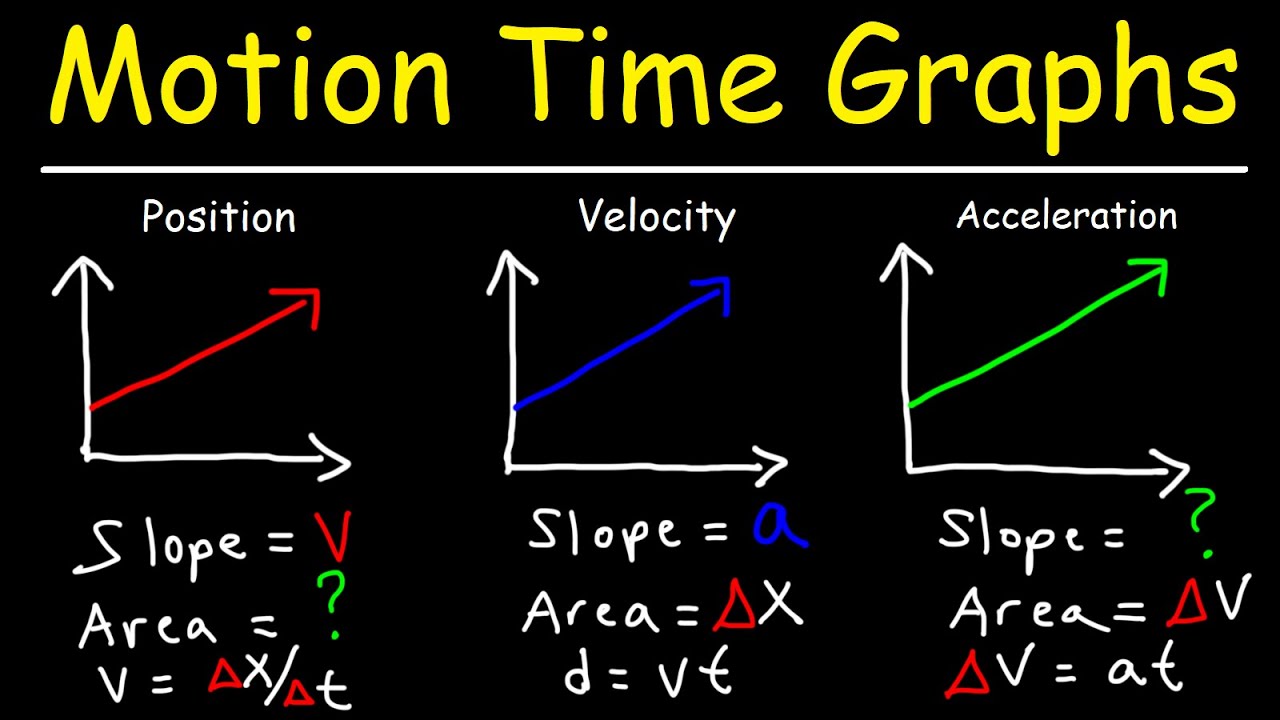
Velocity Time Graphs, Acceleration & Position Time Graphs - Physics

01 - Motion with Constant Acceleration in Physics (Constant Acceleration Equations)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEducationMotionAnalysisVelocityGraphAccelerationConstantCarMovementEducationalContentScienceLearningMathematicsIntegrationKinematicsWorkbookSolutions