01 - Motion with Constant Acceleration in Physics (Constant Acceleration Equations)
TLDRThis lesson delves into one-dimensional motion with constant acceleration, contrasting it with uniform motion and highlighting its complexity. The focus is on understanding the equations of motion for constant acceleration, which are derived and explained through intuitive examples. The velocity-time graph for constant acceleration is a straight line with a slope equal to the acceleration, while the position-time graph is a parabola. The three fundamental equations of motion are introduced, each applicable for solving different types of problems involving constant acceleration, such as calculating final position, final velocity, or relating velocity, acceleration, and displacement.
Takeaways
- 📚 The lesson focuses on one-dimensional motion with constant acceleration, introducing the equations of motion for such scenarios.
- 🏃 Constant acceleration motion is characterized by a change in velocity at a steady, unchanging rate over time.
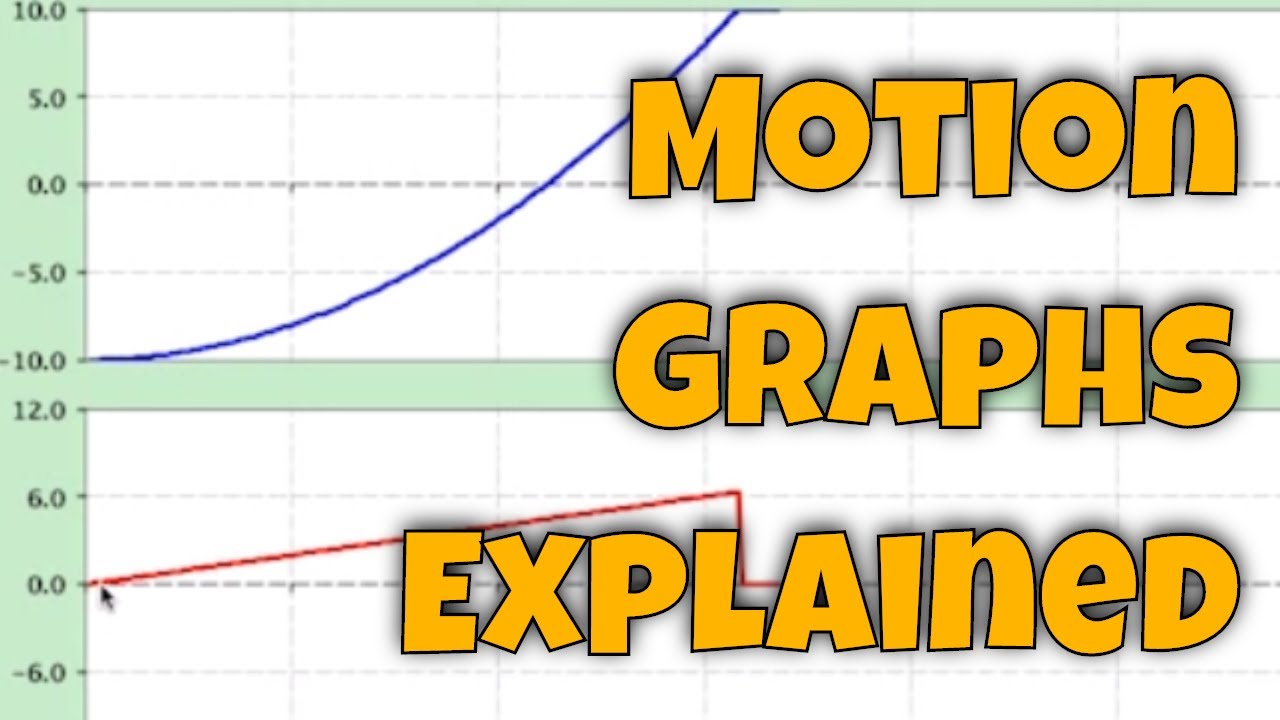
- 📈 In constant acceleration scenarios, the velocity-time graph is a straight line with a slope equal to the acceleration.
- 🚀 The position-Time graph for constant acceleration motion is parabolic, reflecting the varying distances covered at different speeds over time.
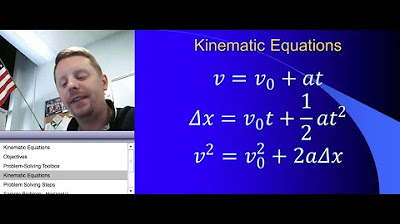
- 📌 The first equation of motion relates position (X) to initial velocity (V naught), time (T), and acceleration (a) as X = V naught T + 1/2 a T squared.
- 🛤️ The second equation of motion expresses velocity (V) as a function of time, given by V = V naught + a T.
- 🌐 The third equation of motion is derived from the first two, eliminating time and relating the final velocity squared to the initial velocity, acceleration, and distance traveled as V squared = V naught squared + 2aX.
- 🔍 These equations are fundamental in physics for solving a variety of problems involving motion, including those under the influence of gravity.
- 📊 The graphical approach to explaining the equations of motion provides an intuitive understanding of why they have the forms they do.
- 🎯 The equations of motion are versatile and can be used to solve for different variables depending on the information provided in a problem.
- 🔄 In practice, one may need to use a combination of the equations and algebraic manipulation to solve for the desired quantities in motion problems.
Q & A
What is the main topic of this physics lesson?
-The main topic of this lesson is the concept of one-dimensional motion with constant acceleration, including an introduction to the equations of motion with constant acceleration.
How does uniform motion differ from motion with constant acceleration?
-Uniform motion involves an object moving at a constant velocity with no acceleration, whereas motion with constant acceleration involves an object speeding up or slowing down at a constant rate, meaning the acceleration does not change throughout the motion.
What is the significance of the term 'constant acceleration' in physics?
-Constant acceleration means that the acceleration of an object remains unchanged throughout the motion. This implies that the object's velocity is increasing or decreasing at a known, steady rate every second.
How does the velocity of an object change over time with constant acceleration?
-With constant acceleration, the velocity of an object increases or decreases by a constant amount each second. This results in a linear relationship between velocity and time, represented by a straight line on a velocity-time graph.
What is the relationship between the slope of the velocity-time graph and acceleration?
-The slope of the velocity-time graph is equal to the acceleration. Since the slope represents the change in velocity over time, a constant slope indicates a constant acceleration.
What does the position-time graph look like for an object undergoing constant acceleration?
-The position-time graph for an object undergoing constant acceleration is a parabola. This is because the object covers smaller distances at the beginning of the motion and larger distances as its velocity increases over time.
What are the three fundamental equations of motion in physics?
-The three fundamental equations of motion are: (1) X = V₀T + 1/2 aT² for position as a function of time, (2) V = V₀ + aT for velocity as a function of time, and (3) V² = V₀² + 2aX for the relationship between final velocity, initial velocity, and displacement.
How can the equations of motion be used to solve problems in physics?
-The equations of motion can be used to solve problems involving constant acceleration, such as calculating the final position, final velocity, or displacement of an object given its initial conditions and acceleration. They are applicable in various scenarios, including straight-line motion and free-fall problems.
Why is it important to understand the equations of motion?
-Understanding the equations of motion is crucial as they form the basis for analyzing and predicting the behavior of objects in motion under constant acceleration. They are fundamental to solving a wide range of physics problems and are also used in more complex areas of physics, such as two-dimensional motion.
What is the role of algebra in applying the equations of motion?
-Algebra is used to manipulate the equations of motion to solve for unknown variables. It allows us to substitute known values into the equations and solve for quantities like acceleration, time, or displacement when they are not directly given in the problem statement.
Outlines
📚 Introduction to Constant Acceleration
This paragraph introduces the concept of constant acceleration in physics, contrasting it with uniform motion. It explains that while uniform motion involves constant velocity, constant acceleration involves a change in velocity at a steady rate, meaning the speed increases or decreases at a constant rate throughout the motion. The lesson aims to provide an intuitive understanding of the equations of motion with constant acceleration, emphasizing the importance of working through examples step by step.
📈 Visualizing Constant Acceleration with Velocity vs. Time Graph
The paragraph discusses the visualization of constant acceleration through a velocity versus time graph. It explains that when acceleration is constant, the velocity increases at a known steady rate every second, resulting in a straight line on the graph. The slope of this line represents the acceleration, and the graph demonstrates that the rate of velocity increase never changes. This understanding helps in grasping the equations of motion for constant acceleration problems.
🚀 Deriving Equations of Motion from Graphical Analysis
This paragraph focuses on deriving the equations of motion from a graphical analysis perspective. It explains that for constant acceleration, the velocity graph is a straight line with a slope equal to the acceleration, and the position graph is a parabola. The paragraph emphasizes the importance of understanding the graphical representation to intuitively grasp the equations of motion, which are fundamental in physics for solving problems involving motion.
🧮 Equations of Motion for Constant Acceleration
The paragraph presents the three fundamental equations of motion for constant acceleration. The first equation relates position to time, the second relates velocity to time, and the third relates the final velocity to the initial velocity, acceleration, and displacement. The explanation highlights how these equations can be used to solve various physics problems involving motion, and how they are derived from the principles of constant acceleration.
🔍 Application and Interpretation of the Equations of Motion
This paragraph discusses the application and interpretation of the equations of motion. It explains how to choose the appropriate equation based on the information provided in a problem and how to use algebra to solve for unknown variables. The paragraph also mentions that these equations are not only applicable to straight-line motion but also to problems involving gravity, such as objects falling from a height. The emphasis is on the practical use of these equations in solving a variety of physics problems.
Mindmap
Keywords
💡One-dimensional motion
💡Constant acceleration
💡Equations of motion
💡Velocity-time graph
💡Position-time graph
💡Initial velocity
💡Acceleration
💡Parabolic trajectory
💡Slope
💡Final velocity
Highlights
The lesson focuses on one-dimensional motion with constant acceleration, providing an overview of the equations of motion.
Uniform motion, with constant velocity, is contrasted with more complex motion involving constant acceleration.
Constant acceleration means the rate of change of velocity remains the same throughout the motion.
The introduction of equations of motion is approached through intuitive understanding rather than just memorization.
The concept of constant acceleration is explained with a real-life example of an object starting with an initial velocity and accelerating at a constant rate.
The velocity-time graph for constant acceleration is a straight line, indicating a linear relationship between velocity and time.
The slope of the velocity-time graph represents the constant acceleration, providing a visual understanding of the concept.
The position-time graph for constant acceleration is a parabola, reflecting the varying distances covered at different speeds.
The first equation of motion relates position to initial velocity, time, and acceleration, and is parabolic in form.
The second equation of motion expresses velocity as a function of initial velocity and time, forming a linear relationship.
The third equation of motion is derived from the first two, eliminating the time variable and relating final velocity, initial velocity, acceleration, and displacement.
These three fundamental equations of motion are essential for solving a wide range of physics problems.
The equations are not only applicable to horizontal motion but also to objects in free fall under gravity.
The lesson aims to provide a deeper intuitive understanding of the equations of motion through practical examples and problem-solving.
The importance of choosing the appropriate equation of motion based on the given information in a physics problem is emphasized.
The lesson concludes with a preview of the next section, where the equations will be further explored and applied to various problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: