Angular Impulse

Bozeman Science
20 Dec 201404:53
EducationalLearning
32 Likes 10 Comments

TLDRIn this informative video, Mr. Andersen explores the concept of angular impulse in physics, defining it as the application of a torque to a rotating system over a specific duration. He uses the example of tether ball to illustrate how a force applied perpendicular to the axis of rotation results in a change in angular momentum. The video further explains the relationship between torque, time, and angular momentum, and differentiates between translational and rotational motion. A practical example involving a motorcross person is used to demonstrate the calculation of angular momentum change, emphasizing the impact of force magnitude and duration. The video concludes with a suggestion to experimentally verify these concepts using a spinning disc and photo gates.

Takeaways
  • 🌀 Angular impulse in physics refers to the application of a force to a rotating system, resulting in a torque.
  • 🏐 Playing tether ball is an example of applying angular impulse, where hitting the ball exerts a torque that changes its angular momentum.
  • 🔄 The change in angular momentum is directly proportional to the torque applied and the duration for which it is applied, known as angular impulse.
  • 🧠 Understanding the difference between translational and rotational motion is crucial for applying the concepts of impulse and angular impulse correctly.
  • 📈 The equation for torque in rotational motion is similar to the equation for force in translational motion, but with rotational inertia and angular acceleration.
  • 🚀 The angular momentum of a rotating system can be changed by applying a torque, which is the product of force, radial distance, and time.
  • 📊 A greater force or applying the force for a longer duration results in a larger change in angular momentum.
  • 🧪 To test the relationship between torque, time, and change in angular momentum, one could use a spinning disc and measure the change with photo gates.
  • 🤔 The right-hand rule can be used to determine the direction of the change in angular momentum.
  • 📚 The concept of angular impulse is an essential part of understanding rotational dynamics in physics.
  • 🎯 The key to solving problems involving angular impulse is to know the torque, the time it is applied, and to be able to calculate the resulting change in angular momentum.
Q & A

  • What is the definition of angular impulse in physics?

    -Angular impulse is the application of a force to a rotating system for a given period of time, which results in the application of a torque.

  • How does playing tether ball illustrate the concept of angular impulse?

    -In tether ball, when you hit the ball, you apply a force perpendicular to the rope, which originates from the center of the rotating system, thus applying a torque and causing a change in the ball's angular momentum.

  • What is the relationship between torque and angular momentum?

    -Torque causes a change in angular momentum. The change in angular momentum is equal to the torque applied multiplied by the time it is applied.

  • How can you determine the direction of the change in angular momentum?

    -The direction of the change in angular momentum can be determined using the right-hand rule.

  • What is the difference between translational and rotational motion?

    -In translational motion, the object moves in a single direction, whereas in rotational motion, the object spins around a center of rotation.

  • How is the equation for torque in rotational motion different from the equation for force in translational motion?

    -In rotational motion, torque is equal to rotational inertia times angular acceleration, whereas in translational motion, force is equal to mass times acceleration.

  • What are the components of the equation for change in angular momentum?

    -The change in angular momentum is composed of torque times the time interval during which the torque is applied.

  • How would applying a greater force or a longer duration of force affect the change in angular momentum?

    -Applying a greater force or applying force for a longer duration would result in a greater change in angular momentum.

  • What is an example of a laboratory setup to test the relationship between torque, time, and change in angular momentum?

    -A laboratory setup could involve a large spinning disc with a force applied perpendicularly to it, and photo gates to measure the change in angular momentum.

  • What is the significance of understanding the relationship between torque, time, and change in angular momentum?

    -Understanding this relationship is crucial for predicting and calculating the effects of forces on rotating systems, which is essential in various applications from sports to engineering.

  • How can the concept of angular impulse be applied in real-world scenarios?

    -The concept of angular impulse can be applied in scenarios like motorcross stunts, where a rider applies force to perform flips, or in machinery where understanding the forces involved in rotation is necessary for design and function.

Outlines
00:00
🌟 Introduction to Angular Impulse in Physics

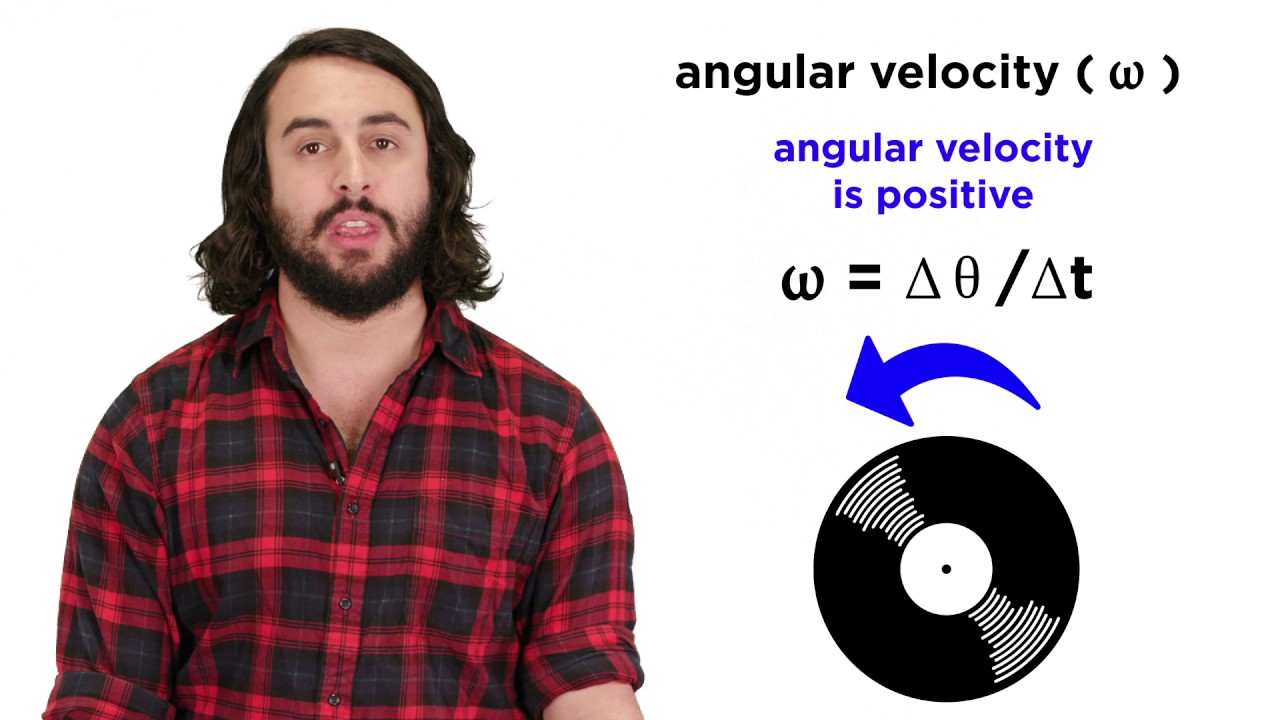
This paragraph introduces the concept of angular impulse in the context of physics, specifically within the realm of AP Physics essentials. Mr. Andersen explains that an impulse in physics is a force applied over a certain duration, and by extension, an angular impulse involves applying a force to a rotating system, effectively applying a torque. The example of tether ball is used to illustrate how a force applied perpendicular to the axis of rotation results in a change in angular momentum. The paragraph emphasizes the relationship between torque, the time it's applied, and the resulting change in angular momentum, setting the stage for a deeper exploration of these principles.

Mindmap
Keywords
💡Angular Impulse
Angular impulse refers to the application of a force to a rotating system over a period of time, resulting in a change in the system's angular momentum. In the context of the video, it is exemplified by applying a force to a tether ball or a motorcross person performing a flip. The concept is integral to understanding how forces affect rotational motion and is calculated as the product of torque and the time over which it is applied.
💡Torque
Torque is the rotational equivalent of linear force and is the cause of angular acceleration. It is defined as the product of the force applied and the perpendicular distance from the axis of rotation to the point where the force is applied. In the video, torque is used to explain how a force can change the angular momentum of a rotating system, such as when a motorcross person applies a force to perform a flip.
💡Angular Momentum
Angular momentum is a measure of the rotational motion of an object and is related to the object's moment of inertia, angular velocity, and the direction of rotation. It is a vector quantity that is conserved in the absence of external torques. In the video, the change in angular momentum is central to understanding the effects of angular impulse, as it is the quantity that changes when a torque is applied over a certain time.
💡Impulse
Impulse in physics is the product of a force and the time over which it acts. It is a measure of the change in momentum of an object and is a vector quantity. In the context of the video, the concept of linear impulse is contrasted with angular impulse to highlight the difference between translational and rotational motion.
💡Rotational Inertia
Rotational inertia, or moment of inertia, is a measure of an object's resistance to changes in its rotational motion. It depends on the mass distribution of the object and its shape. In the video, rotational inertia is used in the equation for torque to show how it relates to angular acceleration and, consequently, to changes in angular momentum.
💡Angular Acceleration
Angular acceleration is the rate of change of angular velocity per unit time. It is a vector quantity that describes how quickly the rotational speed of an object changes. In the video, angular acceleration is a key component in understanding how torque affects the change in angular momentum, as it is the result of a torque being applied to a rotating system.
💡Right Hand Rule
The right-hand rule is a convention used in physics to determine the direction of vectors such as angular momentum and torque. It involves using the right hand to point the fingers in the direction of one vector (like torque) and then curling the fingers to indicate the direction of the associated vector (like the direction of angular momentum).
💡Translational Motion
Translational motion refers to the movement of an object where all parts of the object move in the same direction and at the same speed. It is contrasted with rotational motion in the video to clarify the difference between how impulse affects linear momentum versus how angular impulse affects angular momentum.
💡Momentum Change
Momentum change, or impulse, is the difference in momentum of an object before and after the application of a force. It is calculated as the product of the force applied and the time over which it acts. In the context of the video, the concept is extended to angular momentum, where the change is referred to as angular impulse.
💡Conservation of Angular Momentum
The conservation of angular momentum states that in the absence of external torques, the angular momentum of a system remains constant. This principle is fundamental in understanding the behavior of rotating systems and is central to the discussion in the video about how angular impulse affects the system's angular momentum.
💡Experimental Verification
Experimental verification involves testing a scientific theory or principle through controlled experiments to confirm or refute its validity. In the video, the concept of angular impulse and its effect on angular momentum is suggested to be verified through laboratory experiments involving a spinning disc and photo gates to measure changes in angular momentum.
Highlights

Angular impulse is defined as a force applied to a rotating system over a period of time, which is equivalent to applying a torque.

Torque is a force applied perpendicular to the axis of rotation, such as hitting a tether ball, which results in a change in angular momentum.

The change in angular momentum due to torque is calculated as the product of torque and the time it is applied.

The right-hand rule can be used to determine the direction of the change in angular momentum.

Understanding the difference between translational and rotational motion is crucial for applying the concepts of impulse and momentum correctly.

In translational motion, the impulse is equal to the change in momentum, which is mass times the change in velocity over time.

In rotational motion, torque is related to the rotational inertia and angular acceleration, and the change in angular momentum is the product of torque and time.

A specific problem involving a motorcross person applying a force to perform a flip illustrates the calculation of change in angular momentum.

The torque in the example is calculated as the product of the force, radial distance from the center of rotation, and the time the force is applied.

Applying a greater force or applying it for a longer period of time results in a greater change in angular momentum.

A laboratory test could involve a spinning disc and applying a force to measure the change in angular momentum using photo gates.

The video aims to teach the use of appropriate mathematics to calculate angular impulse and its effect on angular momentum.

The relationship between torque, time, and change in angular momentum can be experimentally tested to verify the theoretical equations.

The concept of angular impulse and its impact on angular momentum is essential for understanding rotational dynamics.

The video provides a clear explanation of how to apply and calculate torque in the context of rotational systems.

Practical applications of angular impulse include sports, such as tether ball, and motorcross stunts.

The video emphasizes the importance of distinguishing between the effects of impulse on translational versus rotational systems.

Transcripts

Browse More Related Video

AP Physics 1 Torque and Rotational Motion Review

Conservation of Angular Momentum

Angular Motion and Torque

Angular Momentum

Angular momentum | Moments, torque, and angular momentum | Physics | Khan Academy

Impulse

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AngularImpulsePhysicsConceptsTorqueExplanationAngularMomentumTetherBallExampleMotorcrossFlipForceApplicationImpulseVsMomentumLabExperimentsEducationalContent