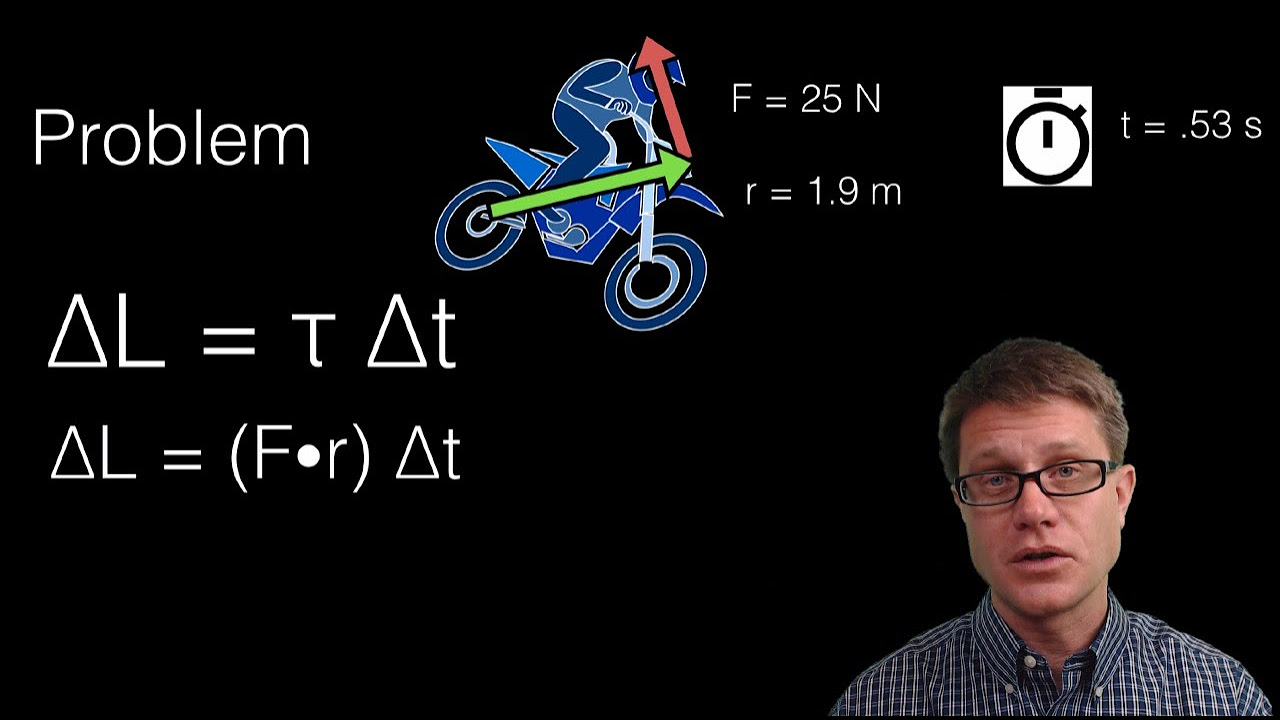Angular Motion and Torque
TLDRIn this engaging video, Professor Dave delves into the intricacies of angular motion, distinguishing between spin and orbital motion, such as the Earth's rotation on its axis and its orbit around the Sun. He introduces key concepts like angular displacement, measured in radians, and its relation to positive or negative rotation. The video also covers angular velocity, defined as the rate of change of angular displacement over time, and angular acceleration, the rate of change of angular velocity. Professor Dave explains how rotational kinematics mirrors linear kinematics but with angular components. He further explores how torque, represented by the Greek letter tau, is the force that sets an object into rotational motion and is maximized when the force is perpendicular to the object's plane. The video concludes with a nod to Archimedes, emphasizing the impact of leverage in generating torque. It's an informative and insightful presentation that brings the principles of angular motion to life.
Takeaways
- 🌀 Angular motion is distinguished into two types: spin (rotation around an internal axis) and orbital motion (rotation around an external axis).
- 🌟 Tangential speed in a rotating object like a Ferris wheel varies with distance from the axis of rotation, but the entire wheel spins at the same speed.
- 📐 Angular displacement (θ) is the angle swept by a line intersecting the axis of rotation and is measured in radians, with one full revolution equaling 2π radians.
- ⏱️ Angular velocity (ω) is the rate of change of angular displacement over time and is measured in radians per second (rad/s).
- ⏰ Angular acceleration (α) is the rate of change of angular velocity over time and is measured in radians per second squared (rad/s²).
- 🔧 Torque (τ) is the force's ability to cause rotational motion around an axis and is calculated as the applied force times the distance (lever arm) times the sine of the angle between the force and the plane of rotation.
- 📏 The longer the lever arm, the greater the torque produced, making it easier to rotate an object.
- ⚖️ Torque is positive for counterclockwise rotation and negative for clockwise rotation, and its sum must be zero for no net rotation.
- 🔄 Rotational kinematics uses equations analogous to linear kinematics, but with angular components replacing linear ones.
- 🌐 The context of rotation (like a solid wheel) may require using angular motion concepts rather than varying tangential speeds.
- 📐 The magnitude of torque is maximized when the force is perpendicular to the plane of the rotating object, as the sine of 90 degrees is one.
- 🌐 Archimedes' quote about moving the Earth with a long enough lever and fulcrum illustrates the principle of torque and the potential for immense rotational force.
Q & A
What is the difference between spin and orbital motion?
-Spin refers to an object rotating around an internal axis that passes through its center of mass. Orbital motion, on the other hand, is when an object orbits around some external axis, such as the Earth spinning on its axis and orbiting around the Sun.
Why is angular motion preferred over translational motion when discussing a rotating rigid object like a Ferris wheel?
-Angular motion is preferred because it allows us to consider the entire rigid object as spinning at the same speed, rather than dealing with varying tangential speeds at different distances from the axis of rotation.
What is angular displacement and how is its direction determined?
-Angular displacement, represented by theta, is the angle swept out by any line passing through a rotating body that intersects the axis of rotation. Its direction is positive if the motion is counterclockwise and negative if clockwise.
What is the SI unit for angular displacement?
-The SI unit for angular displacement is the radian. One full revolution is equal to 2 pi radians.
How is angular velocity defined and what is its SI unit?
-Angular velocity is defined as the angular displacement over a time period, similar to how linear velocity is linear displacement over time. Its SI unit is radians per second.
What is the relationship between angular acceleration and angular velocity?
-Angular acceleration, represented by the Greek letter alpha, is the change in angular velocity over a time period, and is equal to the change in angular velocity (delta omega) over time (delta t), with units of radians per second squared.
How are the equations of rotational kinematics related to those of linear kinematics?
-Rotational kinematics utilizes equations that are direct analogs of those involved with linear kinematics, but with linear components swapped out for angular ones, such as displacement for angular displacement, velocity for angular velocity, and acceleration for angular acceleration.
What is torque and how does it relate to rotational motion?
-Torque is the ability of a force to rotate an object around some axis and is defined as the applied force times the distance over which the force is applied times the sine of the angle between the force vector and the plane of the rotating object. It is what sets a system into rotational motion.
What are the units of torque and when is it at its maximum?
-The units of torque are Newton meters. Torque is at its maximum when the applied force is perpendicular to the plane containing the object, because the sine of 90 degrees is one.
How does the length of the lever arm affect the magnitude of torque?
-The longer the lever arm, the easier it is to produce torque. This is why it is more difficult to push a door open if you press near the hinge compared to pressing further away, as the lever arm is extended.
What does the quote by Archimedes regarding a lever and a fulcrum imply about torque?
-The quote implies that with a long enough lever arm, one could generate a massive torque capable of moving the world, highlighting the principle that increased leverage can result in a significant increase in torque.
Why is it important to consider the direction of rotation when defining torque?
-The direction of rotation is important because it determines whether the torque is positive (counterclockwise rotation) or negative (clockwise rotation), which is crucial for understanding the net effect of multiple forces acting on an object.
Outlines
🌌 Angular Motion Concepts
Professor Dave introduces the topic of angular motion, distinguishing between spin and orbital motion. He explains that while objects can spin around an internal axis, they can also orbit around an external one, using the Earth's rotation and orbit around the Sun as examples. The concept of angular displacement (theta) is introduced as the angle swept out by a line passing through a rotating body that intersects the axis of rotation, with positive values for counterclockwise motion and negative for clockwise. The SI unit for angular displacement is radians, with one full revolution equaling 2 pi radians. Angular velocity (omega) is the rate of angular displacement over time, measured in radians per second. Angular acceleration (alpha) is the rate of change of angular velocity, with units of radians per second squared. The paragraph also covers how rotational kinematics mirrors linear kinematics, with a set of equations for calculating rotational motion under constant angular acceleration. Finally, torque (tau) is defined as the force's ability to rotate an object around an axis, calculated as the applied force times the distance over which the force is applied times the sine of the angle between the force vector and the plane of rotation, with units of Newton meters.
🔧 The Mechanics of Torque
The second paragraph delves into torque, which is the force's ability to cause rotational motion. It is represented by the Greek letter tau and is calculated as the product of the applied force, the distance over which the force is applied, and the sine of the angle (theta) between the force vector and the plane of the rotating object. Torque is maximized when the force is perpendicular to the object's plane, as the sine of 90 degrees is one. The paragraph explains that torque diminishes as the angle deviates from 90 degrees and becomes zero when the angle is zero, resulting in no motion. By convention, torque is considered positive for counterclockwise rotation and negative for clockwise. The concept of equal and opposite torques resulting in no net movement is also discussed. The magnitude of torque is further explained in relation to the length of the lever arm, which is the distance from the axis of rotation to the point where the force is applied. The longer the lever arm, the easier it is to produce torque, exemplified by the difficulty of opening a door when pushing near the hinge versus further out. The paragraph concludes with a nod to Archimedes' famous quote about the power of a lever and a fulcrum, encouraging further exploration of his wisdom.
Mindmap
Keywords
💡Angular Motion
💡Spin
💡Orbital Motion
💡Tangential Speed
💡Angular Displacement
💡Radian
💡Angular Velocity
💡Angular Acceleration
💡Torque
💡Lever Arm
💡Archimedes
Highlights
Angular motion can be categorized into spin and orbital motion. An object can spin around an internal axis and orbit around an external axis.
Uniform circular motion involves tangential speed varying with distance from the axis of rotation.
When analyzing a rotating rigid object like a Ferris wheel, it's more appropriate to discuss angular or rotational motion rather than translational motion.
Angular displacement (θ) is the angle swept out by a line passing through a rotating body that intersects the axis of rotation. Positive for counterclockwise, negative for clockwise motion.
One full revolution equals 2π radians. A counterclockwise quarter turn results in an angular displacement of π/2 radians.
Angular velocity (ω) is the rate of change of angular displacement over time, measured in radians per second.
Counterclockwise rotation results in positive angular velocity, while clockwise rotation results in negative angular velocity.
Angular acceleration (α) is the rate of change of angular velocity over time, measured in radians per second squared.
Rotational kinematics utilizes equations that are direct analogs of linear kinematics, but with angular components.
Torque (τ) is the ability of a force to rotate an object around an axis. It equals the applied force times the distance over which the force is applied, times the sine of the angle between the force vector and the plane of rotation.
Torque is measured in Newton meters and is maximized when the applied force is perpendicular to the plane containing the object.
Torque is positive if it results in counterclockwise rotation and negative if it results in clockwise rotation.
If two forces produce equal and opposite torques on an object, the object will not move and the net torque is zero.
The magnitude of torque equals the magnitude of the applied force times the length of the lever arm (distance from axis of rotation to point of force application).
A longer lever arm makes it easier to produce torque, as demonstrated by pushing a door open being easier the further away from the hinge you push.
Archimedes famously said, "Give me a lever long enough and a fulcrum to place it on, and I will move the earth." This highlights the concept of using a long lever arm to generate massive torque.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: