Conservation of Angular Momentum

Bozeman Science
6 Apr 201505:38
EducationalLearning
32 Likes 10 Comments

TLDRIn this informative video, Mr. Andersen explores the concept of angular momentum conservation, differentiating it from linear momentum. He explains that angular momentum is associated with rotation and remains constant unless acted upon by an external torque. The video delves into calculating angular momentum for point objects and extended objects, using equations involving radius, linear momentum, moment of inertia, and angular velocity. Mr. Andersen illustrates the conservation principle with examples like a tether ball and a figure skater, showing how changes in radius or moment of inertia affect rotational speed. The video concludes with a challenge problem, encouraging viewers to apply their understanding of angular momentum to real-world scenarios.

Takeaways
  • 🌐 Angular momentum is a principle that explains the rotation of objects, like Earth, due to conservation from the formation of the solar system.
  • 🔄 The conservation of angular momentum holds true as long as there is no net external torque acting on an object or system.
  • 🔺 Angular momentum differs from linear momentum as it is associated with rotation, while linear momentum is related to linear motion.
  • 📏 For a point object in rotation, angular momentum is calculated as the radius times the linear momentum of the object (mass times velocity).
  • 🔄 For an extended object, angular momentum is calculated using the moment of inertia (mass distribution) times the angular velocity.
  • ⚖️ Analogous to linear momentum in collisions, angular momentum can also be transferred between objects in a rotating system.
  • 🎢 When the radius of rotation decreases, the angular velocity increases to conserve angular momentum, causing the object to spin faster.
  • 🏆 Figure skaters demonstrate the conservation of angular momentum by increasing their spin speed when they pull their arms in, reducing their moment of inertia.
  • 🔢 Qualitative and quantitative calculations can be made to understand changes in angular momentum due to alterations in radius or moment of inertia.
  • 📌 The Earth is gradually slowing down due to the conservation of angular momentum, but this process is not a cause for concern in the near future.
  • 💡 Understanding the conservation of angular momentum is crucial for making predictions about the behavior of rotating or orbiting objects.
Q & A

  • What is the main concept discussed in the video?

    -The main concept discussed in the video is the conservation of angular momentum.

  • How is angular momentum different from linear momentum?

    -Angular momentum is due to rotation, whereas linear momentum is associated with the linear motion of an object.

  • Why does the Earth continue to rotate?

    -The Earth continues to rotate due to the conservation of angular momentum from the formation of the solar system.

  • What happens when the radius of rotation decreases while angular momentum is conserved?

    -When the radius decreases and angular momentum is conserved, the linear velocity (speed) of the object increases.

  • How is angular momentum calculated for a point object in rotation?

    -For a point object in rotation, angular momentum is calculated as the product of the radius, mass, and linear velocity (r * p).

  • How is angular momentum calculated for an extended object?

    -For an extended object, angular momentum is calculated as the product of the moment of inertia (I) and angular velocity (omega).

  • What is the effect of a figure skater pulling in their arms while rotating?

    -When a figure skater pulls in their arms, they decrease their moment of inertia, which results in an increase in angular velocity (speed) to conserve angular momentum.

  • What happens to the angular momentum of a rotating object when an external force is applied?

    -The angular momentum of a rotating object will change if an external torque is applied, as this will alter the net external torque acting on the object.

  • How does the conservation of angular momentum apply to a tether ball rotating with a shortened radius?

    -When the radius of a tether ball is shortened, the angular momentum remains constant, resulting in an increase in the ball's linear velocity (speed).

  • What is the relationship between the moment of inertia and angular velocity in an object with constant angular momentum?

    -If the moment of inertia decreases (or increases), the angular velocity must increase (or decrease) to conserve angular momentum, assuming no external torque is acting.

  • How can the conservation of angular momentum be used to predict the behavior of rotating objects?

    -The conservation of angular momentum can be used to predict that if the moment of inertia or radius of rotation changes, the angular velocity will adjust to maintain the same angular momentum, assuming no external torque.

Outlines
00:00
🌐 Introduction to Angular Momentum Conservation

This paragraph introduces the concept of angular momentum conservation, distinguishing it from linear momentum by focusing on rotation. It explains that the Earth's rotation is due to the conservation of angular momentum from the formation of the solar system, although it is gradually slowing down. The explanation continues with the calculation of angular momentum for point objects and extended objects, emphasizing that angular momentum is conserved in the absence of net external torque. Analogies are drawn between linear and angular momentum, particularly during collisions, and the calculation of angular momentum for a rotating disc is discussed using the equation L = I * omega. The paragraph concludes with a qualitative example of how changing the radius in a tether ball system affects speed, illustrating the conservation of angular momentum.

05:02
📚 Quantitative Analysis and Applications of Angular Momentum

The second paragraph delves into the quantitative aspect of angular momentum, encouraging viewers to understand the calculations related to angular momentum when no net external torque is acting on a system. It poses a question about the behavior of extended and point objects under the conservation of angular momentum. The paragraph uses the example of a figure skater to explain how reducing the moment of inertia by pulling in arms increases angular velocity, conserving angular momentum. A quantitative calculation is provided, demonstrating how halving the radius of a system doubles the final velocity, maintaining angular momentum. The paragraph ends with a challenge for the viewer to apply this knowledge to a rotating disc scenario, with a prompt to solve for changes in angular velocity when a disc is dropped on another spinning disc, with the solution provided in the video description.

Mindmap
Keywords
💡Angular Momentum
Angular momentum is a measure of the rotational motion of an object. It is a vector quantity that depends on the object's moment of inertia, its angular velocity, and the direction of rotation. In the context of the video, angular momentum is conserved when no net external torque acts on an object or system, such as the Earth's continued rotation due to the conservation of angular momentum from the formation of the solar system.
💡Conservation of Angular Momentum
The principle of conservation of angular momentum states that the angular momentum of a system remains constant if no external torque acts on it. This is a fundamental concept in physics that helps explain phenomena such as the spinning of a figure skater pulling in their arms or the tether ball increasing its speed when the radius is shortened.
💡Linear Momentum
Linear momentum is the product of an object's mass and its velocity in a straight line. It is a vector quantity and is conserved during collisions when no external forces are acting on the system. The video contrasts linear momentum with angular momentum, highlighting the difference in how they are calculated and conserved.
💡Moment of Inertia
The moment of inertia is a measure of an object's resistance to rotational motion about a particular axis. It depends on the mass of the object and how that mass is distributed relative to the axis of rotation. In the video, the moment of inertia is used in the calculation of angular momentum for extended objects, such as a rotating disc or a figure skater.
💡External Torque
An external torque is a force that causes or changes the rotational motion of an object. When no net external torque acts on an object or system, the angular momentum is conserved. The video emphasizes that the conservation of angular momentum is directly related to the absence of external torques.
💡Rotation
Rotation refers to the motion of an object turning around a fixed axis or point. In physics, rotation is a key concept for understanding angular momentum. The video discusses rotation in the context of both point objects, like a tether ball, and extended objects, like a figure skater or a rotating disc.
💡Point Object
A point object is an idealization in physics where an object with mass is considered to be concentrated at a single point. This simplification is used to calculate angular momentum for such objects in rotation by relating it to the object's mass, the radius of rotation, and its linear velocity.
💡Extended Object
An extended object is a physical body that takes up space and has a size and shape. In the context of the video, the angular momentum of an extended object is calculated differently than that of a point object, using the object's moment of inertia and angular velocity.
💡Angular Velocity
Angular velocity is the rate at which an object rotates around an axis. It is a scalar quantity and is measured in radians per second. The video links angular velocity to the calculation of angular momentum, especially for extended objects.
💡Tether Ball
A tether ball is a game in which a ball is attached to a string and players hit the ball, causing it to rotate around a vertical axis. In the video, the tether ball is used as an example to illustrate the conservation of angular momentum and the effects of changing the radius of rotation on the ball's speed.
💡Figure Skater
A figure skater is an athlete who performs on ice, executing various jumps, spins, and movements. In the context of the video, the figure skater is used to demonstrate how the conservation of angular momentum applies to extended objects, particularly when the skater changes the distribution of their mass during a spin.
Highlights

Angular momentum is different from linear momentum as it is due to rotation.

The Earth continues to rotate due to the conservation of angular momentum from the formation of the solar system.

Angular momentum is maintained as long as there is no net external torque acting on an object or system.

Angular momentum can be calculated in two ways: for a point object in rotation or for an extended object.

For a point object, angular momentum equals the radius times the linear momentum of the object.

For an extended object, angular momentum equals the moment of inertia times the angular velocity.

The conservation of angular momentum states that the angular momentum before equals the angular momentum after, if no external torque acts on the system.

Analogs of linear momentum apply to angular momentum, such as momentum transfer during collisions.

The formula for calculating angular momentum of a rotating disc is L = I times omega.

When the radius is shortened in a rotating system, the speed increases to conserve angular momentum.

A figure skater spinning faster when pulling in their arms is an example of conserving angular momentum by decreasing the moment of inertia.

The qualitative prediction of what happens to an object's angular velocity when its moment of inertia changes can be understood through the conservation of angular momentum.

Quantitative calculations can be made to determine the effects of changes in radius or moment of inertia on angular momentum.

An example calculation is provided where the radius is halved, and the resulting change in velocity is determined.

The video discusses the application of angular momentum principles to both point objects and extended objects like discs and figure skaters.

The conservation of angular momentum principle is fundamental to understanding the behavior of rotating objects and systems.

The video aims to help viewers understand qualitative predictions and quantitative calculations related to angular momentum under no net external torque.

Transcripts

Browse More Related Video

What Is Angular Momentum?

Angular Momentum

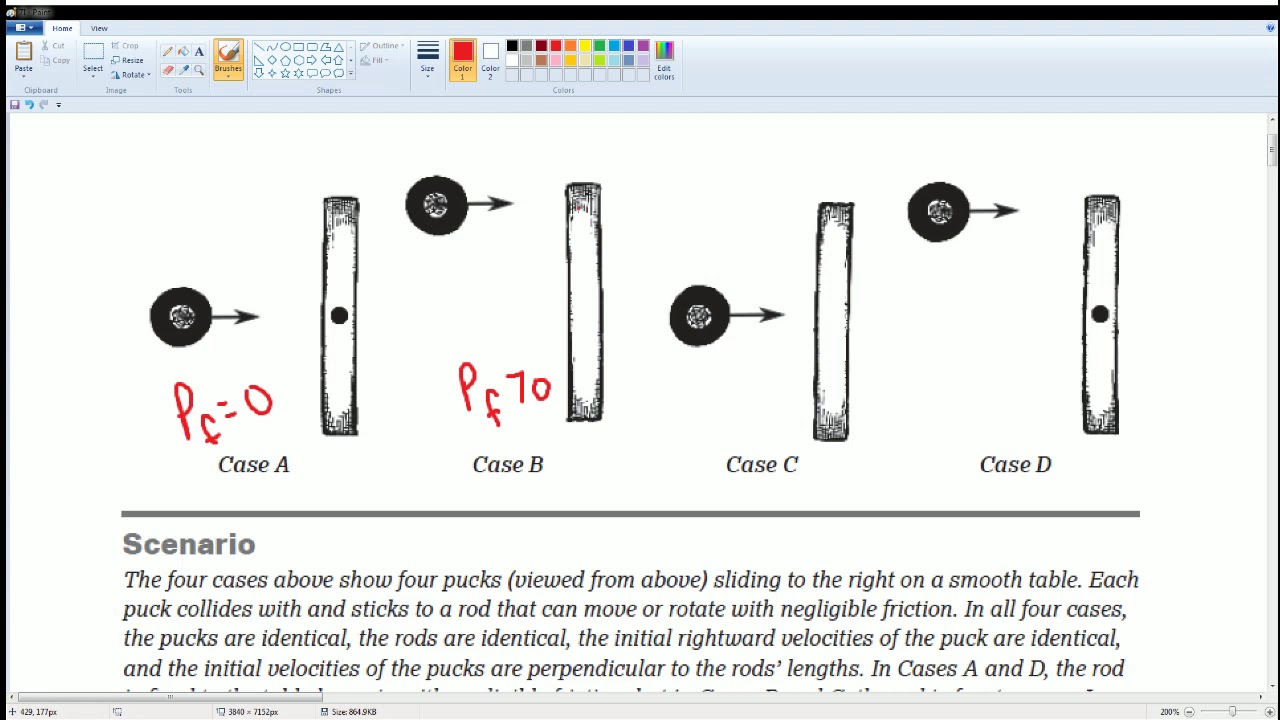
AP Physics Workbook 7.I Collisions "Old and Lack Full Explanation"

Rotation Free Response Paragraph Questions (AP Physics 1)

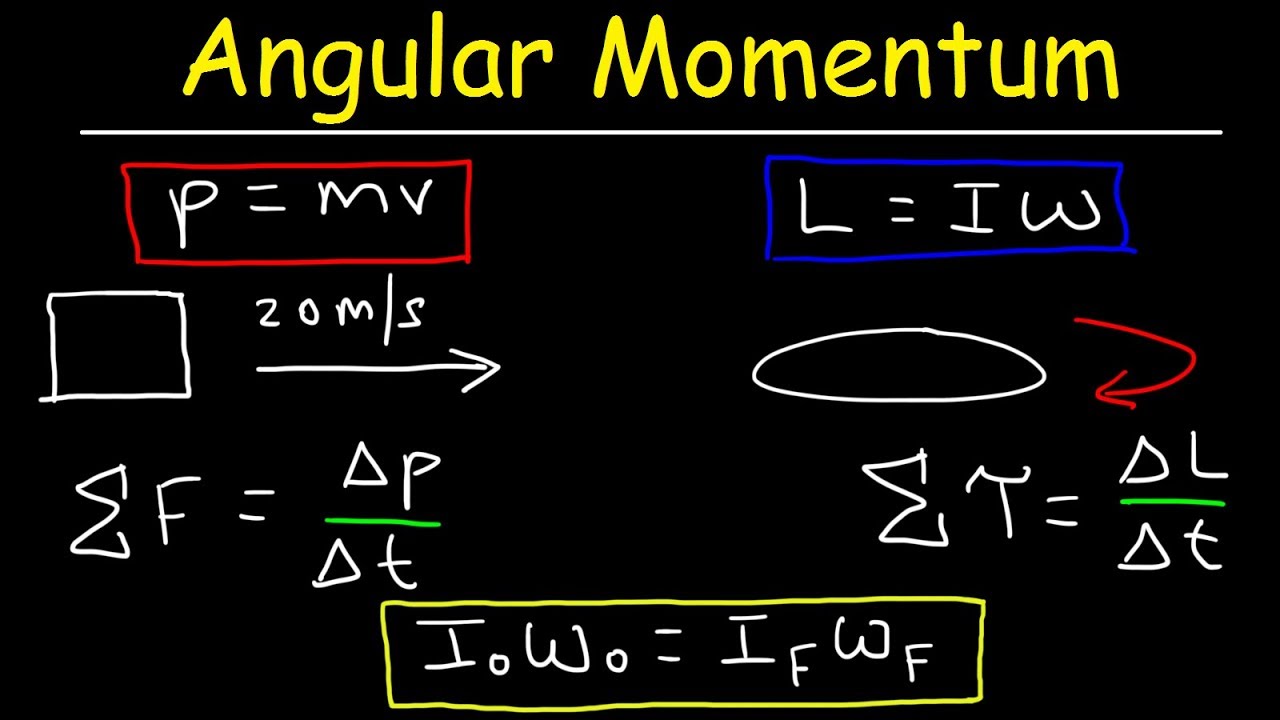
Angular Momentum - Basic Introduction, Torque, Inertia, Conservation of Angular Momentum

Conservation of Angular Momentum | Physics with Professor Matt Anderson | M12-18

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AngularMomentumPhysicsPrinciplesConservationLawsEarthRotationSkatingMotionMomentumAnalogsRotationalDynamicsMomentInertiaPhysicsEducationAPPhysics