Calculus grade 12: Exam

Kevinmathscience
28 Oct 202114:32
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a detailed walkthrough of solving a cubic equation to find its y-intercept, x-intercepts, and turning points. It begins by identifying the y-intercept as (0,1) and then demonstrates the process of finding x-intercepts using factors and synthetic division, revealing the values x = -1 and x = 1. The script humorously clarifies that the formula for the vertex of a parabola does not apply to cubics and proceeds to find the turning points by setting the first derivative to zero, resulting in x = 1 and x = -1/3. It concludes with a discussion on sketching the graph, indicating intercepts and turning points, and determining intervals where the first derivative is negative, both graphically and mathematically.

Takeaways
  • 📚 The script discusses finding the y-intercept of a cubic equation by setting x to zero and solving for y, resulting in the point (0, 1).
  • 🔍 To find the x-intercepts, the script suggests setting y to zero and using factors of the constant term to find potential x values that result in a zero value for the equation.
  • 🔢 The script mentions using synthetic division as a method to find x-intercepts, which is a technique often taught in algebra courses.
  • 📉 The x-intercepts are found to be at x = -1 and x = 1, indicating that the cubic function crosses the x-axis at these points.
  • 🔄 The script notes that when x-intercepts repeat, it indicates a turning point on the graph, which is an important aspect to consider when sketching the function.
  • 📈 The turning point of the cubic function is not found using the formula for parabolas (-b/2a) but by setting the first derivative equal to zero and solving for x.
  • 📝 The first derivative of the cubic function is calculated to be 3x^2 - 2x - 1, which is then set to zero to find the x-values of the turning points.
  • 📊 The script uses both the graph and the mathematical approach to determine where the first derivative is less than zero, indicating where the function is decreasing.
  • 📐 The turning points are found to be at x = 1 and x ≈ -1/3, with corresponding y-values calculated from the original equation.
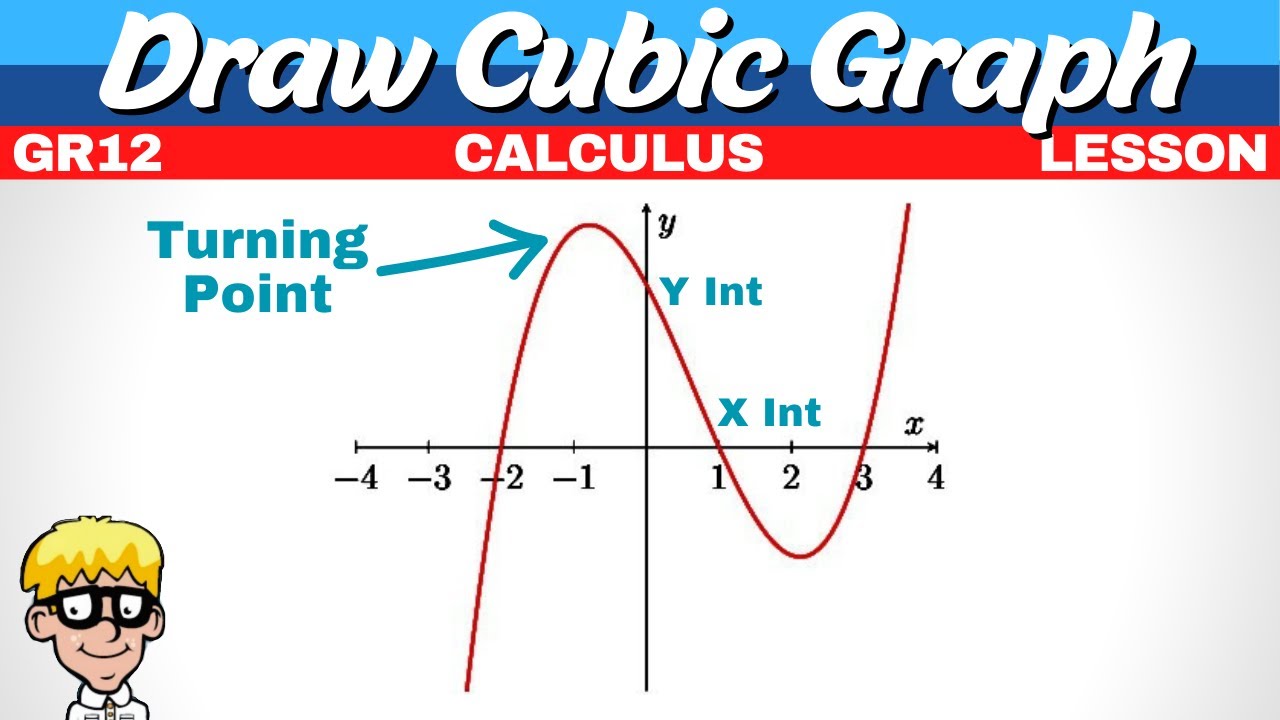
  • 🖋️ The script instructs to sketch the graph of the function, clearly indicating all intercepts and turning points, and to label the coordinates.
  • 📋 The final task in the script is to write down the values of x for which the first derivative is less than zero, which can be determined from the graph or by solving the inequality.
Q & A

  • What is the y-intercept of a cubic equation?

    -The y-intercept is found by setting x equal to zero in the equation. In the provided script, the y-intercept is at the coordinates (0, 1).

  • How do you find the x-intercepts of a cubic equation?

    -To find the x-intercepts, set y to zero and solve for x. The script suggests using factors of the constant term or synthetic division to find possible x values that result in zero.

  • What is the block method mentioned in the script?

    -The block method is a technique for finding x-intercepts of a cubic equation, though the script does not provide a detailed explanation of this method.

  • What is the first step in finding the x-intercepts of a cubic equation as described in the script?

    -The first step is to find an x value that works, which means finding a value of x that, when substituted into the equation, results in y being zero.

  • What is the significance of the repeating x-intercept in the context of the cubic equation discussed in the script?

    -A repeating x-intercept indicates a turning point in the graph of the cubic equation, which is an important feature to note when analyzing the graph.

  • How can you find the turning point of a cubic equation?

    -The turning point can be found by taking the first derivative of the equation, setting it equal to zero, and solving for x. Then, substitute the x value back into the original equation to find the corresponding y value.

  • What is the difference between the method to find the turning point of a cubic equation and that of a quadratic equation?

    -For a quadratic equation, the turning point can be found using the formula -b/(2a). However, for a cubic equation, the first derivative must be set to zero and solved for x, and then the x value is substituted back into the original equation to find the y value of the turning point.

  • What is the first derivative of the cubic equation discussed in the script?

    -The first derivative of the cubic equation, as mentioned in the script, is 3x^2 - 2x - 1.

  • How can you determine where the graph of a cubic equation is decreasing?

    -The graph of a cubic equation is decreasing where the first derivative is less than zero. This can be determined either by analyzing the graph or by solving the inequality formed by the first derivative.

  • What are the x values for which the first derivative of the cubic equation is less than zero, according to the script?

    -The x values for which the first derivative is less than zero are between the x values of the turning points, which are greater than -1/3 and less than 1.

  • How does the script suggest sketching the graph of the cubic equation?

    -The script suggests using the found intercepts and turning points to sketch the graph, ensuring all these points are clearly indicated and the graph's behavior is accurately represented.

Outlines
00:00
📚 Calculus Question - Finding Intercepts and X-Intercepts

The speaker begins by addressing a calculus question involving a cubic equation. They explain the process of finding the y-intercept by setting x to zero, resulting in the coordinates (0, 1). The focus then shifts to finding the x-intercepts, where the speaker mentions various methods, including the 'block method' and synthetic division, to find the roots of the equation. They demonstrate the basic approach by plugging in factors of the constant term to find x equals -1 as a solution. The speaker encourages students to review textbook material or online courses for a deeper understanding of factorizing cubic equations.

05:00
🔍 Factorizing the Cubic Equation and Finding Turning Points

Continuing from the previous explanation, the speaker outlines the steps to factorize the cubic equation after finding an x-intercept of -1. They use the factors of the constant term to deduce the coefficients a, b, and c, resulting in the trinomial being factorized into (x - 1)(x - 1). The speaker then discusses the concept of turning points in cubic equations, noting the incorrect application of the formula for the vertex of a parabola and instead using the first derivative set to zero to find the x-values of the turning points. They solve the derivative equation to find x equals 1 and x equals -1/3, and then calculate the corresponding y-values to determine the coordinates of the turning points.

10:02
📈 Sketching the Graph and Analyzing the Gradient

The speaker concludes the lesson by instructing how to sketch the graph of the function, emphasizing the importance of indicating all intercepts and turning points. They provide the coordinates for the y-intercept, x-intercepts, and turning points, and describe the general shape of the graph, including its increasing and decreasing intervals. The speaker also explains how to determine where the first derivative is less than zero, both graphically by identifying the decreasing sections of the graph and mathematically by solving the inequality formed by the first derivative. They highlight the importance of understanding the gradient's sign to determine the intervals of increase and decrease.

Mindmap
Keywords
💡Cubic Equation
A cubic equation is a polynomial equation of degree three. It is the main subject of the video script, where the host is explaining how to find the y-intercept and x-intercepts of such an equation. The script mentions a cubic equation as the starting point for the discussion, indicating that it is a fundamental concept in calculus and algebra.
💡Y-Intercept
The y-intercept is the point where a graph of a function intersects the y-axis. In the context of the video, the host explains that to find the y-intercept of a cubic equation, one must set x to zero and solve for y, resulting in the coordinates (0, 1) in this case. This concept is crucial for understanding the behavior of the function at the origin.
💡X-Intercept
The x-intercepts are the points where a graph of a function intersects the x-axis. The host discusses various methods to find x-intercepts, including synthetic division and factoring, and identifies the x-intercepts of the given cubic equation as (1, 0) and (-1, 0). This is an essential part of analyzing the function's roots.
💡Synthetic Division
Synthetic division is a method used for polynomial division, particularly useful for finding the roots of polynomials. The script mentions synthetic division as a potential tool for finding x-intercepts, although it does not demonstrate it in detail. It is an efficient technique for simplifying the process of dividing polynomials.
💡Factorizing
Factorizing, or factoring, is the process of breaking down a polynomial into a product of its factors. In the script, the host uses factorizing to simplify the cubic equation into a product of binomials, which helps in finding the x-intercepts and understanding the function's structure.
💡Turning Point
A turning point is a point on the graph of a function where the concavity changes. The host explains that the turning point of a cubic equation can be found by setting the first derivative equal to zero and solving for x. In the video, the turning points are identified as (1, 0) and (-1/3, 1.9), which are critical for sketching the graph's shape.
💡First Derivative
The first derivative of a function measures its rate of change or slope at a given point. The script discusses finding the first derivative of the cubic equation, which is 3x^2 - 2x - 1, to determine the turning points and where the function is increasing or decreasing.
💡Quadratic Formula
The quadratic formula is used to solve quadratic equations of the form ax^2 + bx + c = 0. Although the host mentions it in the context of solving for x when the first derivative is set to zero, the actual derivative in the script is not a quadratic equation, but the formula is a fundamental tool in algebra.
💡Gradient
In the context of the video, the gradient refers to the slope of the tangent to the graph of a function at a given point, which is the same as the first derivative. The host uses the term to explain how to find the turning points and where the function is decreasing, which is essential for graphing and analyzing the function's behavior.
💡Inequality
An inequality is a mathematical statement that relates expressions that are not necessarily equal, using symbols such as 'less than' or 'greater than'. The script suggests using an inequality to find the range of x values for which the first derivative is negative, indicating where the function is decreasing.
💡Interval Notation
Interval notation is a way to express a set of numbers with a lower and upper bound. The host uses interval notation to describe the range of x values where the first derivative is negative, providing a clear and concise way to communicate the intervals where the function's gradient is negative.
Highlights

Introduction to a calculus problem involving a cubic equation.

Explanation of finding the y-intercept by setting x to zero and obtaining a y value of 1.

Clarification that the y-intercept coordinates are (0, 1).

Discussion on calculating x-intercepts by setting y to zero and using the block method.

Mention of synthetic division as a method for finding x-intercepts.

Identification of x-intercept at x = -1 using trial and error with factors.

Use of brackets to simplify the cubic equation after finding an x-intercept.

Explanation of how to determine coefficients a, b, and c after factoring.

Identification of the cubic equation as factoring into (x - 1)(x - 1).

Note on the significance of repeating x-intercepts indicating a turning point.

Calculation of the turning point using the first derivative set to zero.

Solution of the first derivative equation using the quadratic formula.

Determination of the y-values for the turning points by plugging x-values into the original equation.

Sketching the graph of the function with all intercepts and turning points indicated.

Explanation of how to determine where the first derivative is less than zero using the graph.

Alternative mathematical approach to finding where the first derivative is less than zero.

Transcripts

Browse More Related Video

Draw Cubic Graph Grade 12

Draw Cubic Graph Grade 12

Calculus Grade 12 Exam Questions

Calculus Grade 12 Exam Questions

How To Find The Equation of a Secant Line

Calculus Grade 12: Practice

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Cubic EquationsY-InterceptX-InterceptsTurning PointGraph SketchingCalculus BasicsEducational ContentMath TutorialGradient AnalysisSynthetic DivisionQuadratic Formula