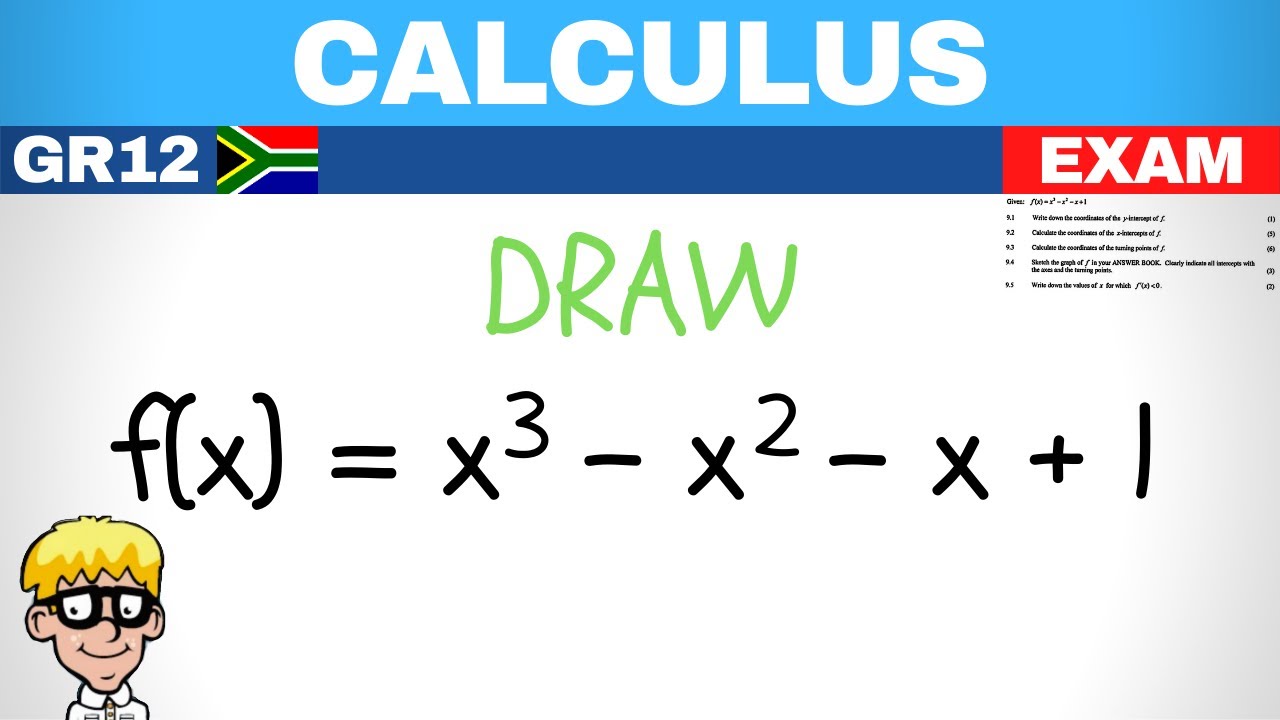Calculus Grade 12 Exam Questions
TLDRThis educational script discusses the process of determining the equation of a parabola given its first derivative and x-intercepts. It explains two methods for finding the parabola's equation: using x-intercepts and turning points. The script guides through calculating the equation, finding turning points, and graphing the function, including intercepts and tangents. It also explores the conditions for lines to be tangents to the parabola and how the intersection point's y-value affects tangency.
Takeaways
- 📚 The script discusses finding the equation of a parabola using x-intercepts and turning points, highlighting two methods from grade 11 knowledge.
- 🔍 It emphasizes the importance of not forgetting the 'a' value when using x-intercepts to derive the parabola equation.
- 📝 The process of finding the 'a' value involves substituting x-intercepts into the equation and solving for 'a', which in the example is found to be -3.
- 📉 The script explains how to graph the first derivative of a function and use it to determine turning points, which are also the x-values where the derivative equals zero.
- 📌 Turning points' coordinates are found by substituting the x-values back into the original function to find the corresponding y-values.
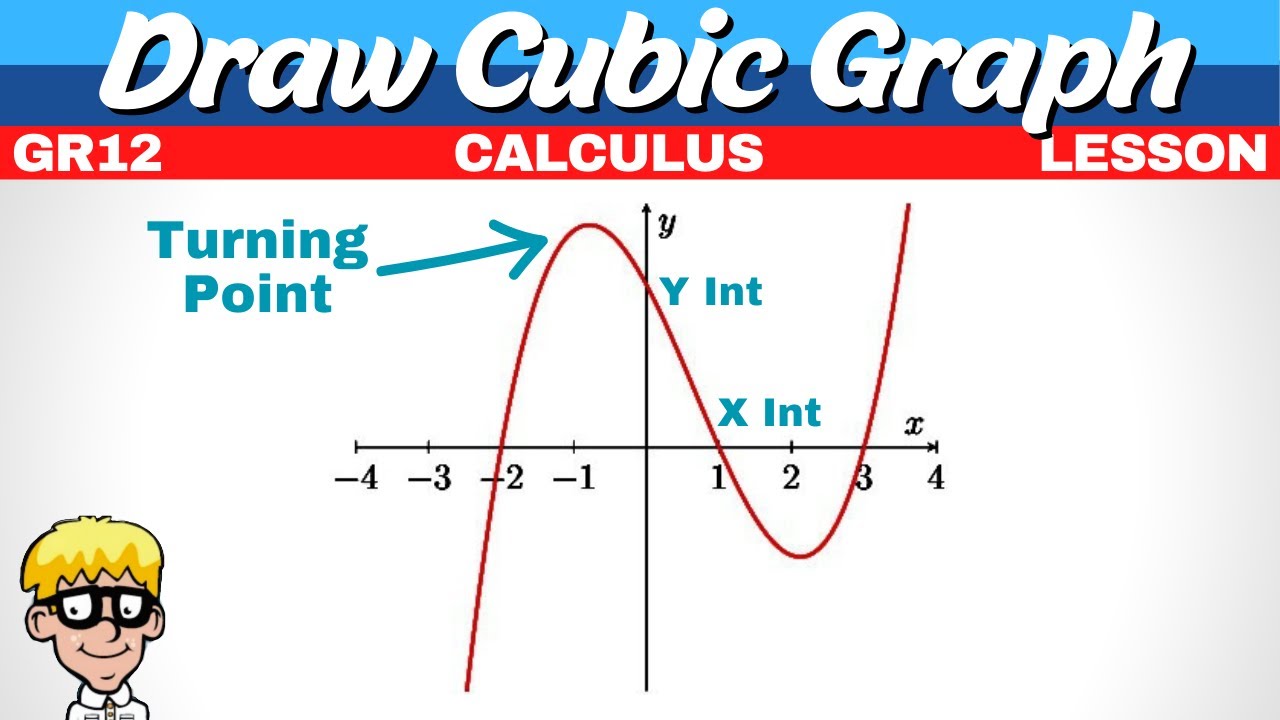
- 📈 The script covers how to graph a cubic function, including finding intercepts and turning points, and plotting them on the graph.
- 🔢 It demonstrates solving for x-intercepts by setting the equation to zero and using methods like synthetic division or factorization.
- 🤔 The script presents a scenario with variable points E and W on the parabola, which are on the same horizontal line, and tangents H and G at these points.
- 📐 It discusses the concept of tangents to a curve, explaining that they must touch the curve at exactly one point and have the same slope as the curve at that point.
- 🏁 The script concludes with a problem involving the conditions under which the lines H and G would no longer be tangents to the parabola, which is when they intersect below the turning point.
- 📝 Lastly, it provides a method to determine the value of 'B' for which the lines H and G would no longer be tangents by comparing it to the y-value of the turning point.
Q & A
What is the first step in finding the equation of a parabola given its x-intercepts?
-The first step is to set up the equation of the parabola in the form y = ax(x - x1)(x - x2), where x1 and x2 are the x-intercepts, and 'a' is a coefficient that will be determined later.
How do you determine the value of 'a' in the parabola equation when given x-intercepts?
-You can determine 'a' by substituting another point on the parabola into the equation and solving for 'a'. This typically involves substituting the x and y values of a point into the equation and simplifying to find the value of 'a'.
What is the significance of the first derivative in the context of the given script?
-The first derivative of a function gives the slope of the tangent to the curve at any point. In the script, the first derivative is used to find the turning points of the original cubic graph.
How can you find the turning points of a cubic graph?
-To find the turning points, you set the first derivative equal to zero and solve for the x-values where the slope of the tangent is zero, indicating a turning point.
What are the coordinates of the turning points if the first derivative is given by -3x^2 + 2x + 1?
-The x-values of the turning points can be found by solving -3x^2 + 2x + 1 = 0. The y-values are then found by substituting these x-values back into the original cubic equation.
How do you find the y-intercept of a cubic function?
-To find the y-intercept, set x = 0 in the equation of the cubic function and solve for y, which will give you the y-coordinate of the y-intercept.
What is the method to find the x-intercepts of a cubic function?
-To find the x-intercepts, set y = 0 in the equation and solve for x. This may involve factoring, using the quadratic formula if it simplifies to a quadratic, or numerical methods if it does not factor easily.
What does the script imply about the relationship between the x-intercepts and the turning point of a parabola?
-The script implies that the turning point of a parabola can be estimated by taking the midpoint of the x-intercepts, although the exact turning point is found by using the formula x = -b/(2a) for a parabola in the form y = ax^2 + bx + c.
How can you determine if a line is a tangent to a curve at a given point?
-A line is a tangent to a curve at a given point if it has the same slope as the curve at that point and intersects the curve at exactly one point.
What is the condition for two lines to be tangents to a parabola at two different points?
-Two lines are tangents to a parabola at two different points if they touch the parabola at those points without crossing it, and the slope of the parabola at each point matches the slope of the respective tangent line.
How does the script describe the process of finding the equation of a tangent line to a parabola at a given point?
-The script suggests using the first derivative to find the slope of the tangent at a given point and then using the point-slope form of a line to find the equation of the tangent line.
Outlines
🔢 Solving Parabolic Equations with X-Intercepts
This paragraph focuses on solving a parabolic equation by using X-intercepts. The first derivative is discussed, with emphasis on finding the values of M, N, and K by plugging in the X-intercepts into the standard equation format. The process involves multiplying the brackets, simplifying the expression, and eventually identifying the coefficients for M, N, and K. The paragraph also highlights common mistakes learners make, such as forgetting the 'a' value, and provides detailed steps for solving the equation.
📊 Calculating Turning Points on a Cubic Graph
This section delves into calculating the turning points of a cubic graph, starting with making the first derivative equal to zero. It explains how to determine the X-values at which the graph equals zero and the method to find the corresponding Y-values by substituting these X-values back into the original equation. The paragraph concludes with instructions on how to plot these points on the graph and emphasizes the importance of correctly identifying the turning points and intercepts for graph accuracy.
🧮 Finding X-Intercepts and Handling Complex Roots
In this paragraph, the focus shifts to finding the X-intercepts of a cubic function, specifically using synthetic division or block method for solving. The process begins by guessing values for X and applying the synthetic division method to simplify the equation. The paragraph explains that after finding one intercept, the remaining quadratic may not have real roots, indicating no further X-intercepts. This leads to the realization that the cubic graph has only one X-intercept, and it explains how to graph this function accurately.
📐 Tangent Lines and Their Intersection Points
The final paragraph discusses the properties of tangent lines at specific points on a parabola and their intersections. It explores the concept of two points on the same horizontal line and how tangents drawn at these points intersect above the parabola's turning point. The paragraph also explains how to determine the X-value of the intersection and the conditions under which the tangents will no longer meet, depending on the B-value of the intersection point. The explanation is detailed, providing insights into how tangent lines behave and the importance of their intersection points in graph analysis.
Mindmap
Keywords
💡First Derivative
💡Parabola
💡X-Intercept
💡Turning Point
💡Cubic Function
💡Equation of a Parabola
💡Y-Intercept
💡Tangent
💡Variable Points
💡Slope
Highlights
Introduction of a method to determine the values of M, N, and K using the graph of the first derivative and x-intercepts.
Explanation of two different ways to find a parabola equation: using x-intercepts or turning points.
Emphasis on not forgetting the 'a' value when using x-intercepts to find the parabola equation.
Demonstration of finding the equation of a parabola using the x-intercepts and a given point on the graph.
Process of solving for the value of 'a' by using the equation derived from the x-intercepts and a graph point.
Derivation of the final parabola equation using the calculated value of 'a'.
Identification of the values of M, N, and K from the derived parabola equation.
Introduction of a problem involving the original cubic graph and the determination of turning points.
Explanation of how to find turning points by setting the first derivative equal to zero.
Use of the graph to identify x-values of turning points without calculating y-values.
Process of finding y-values for the turning points by substituting x-values into the original graph equation.
Task of drawing the graph of 'f' with indicated turning points and intercepts for a comprehensive understanding.
Method for finding the y-intercept by setting x to zero in the equation of 'f'.
Approach to finding x-intercepts by setting y to zero and solving the derived equation.
Discussion of different methods to find x-intercepts, including synthetic division and the block method.
Explanation of the block method for solving the x-intercepts of a cubic equation.
Illustration of an alternative method to the block method for finding x-intercepts without synthetic division.
Identification of the single x-intercept for the given cubic equation and its location on the graph.
Introduction of a scenario involving variable points E and W on the same horizontal line and tangents H and G.
Analysis of the conditions under which H and G would no longer be tangents to the parabola.
Calculation of the x-value of the turning point using the formula B/2A for a parabola.
Determination of the y-value of the turning point by substituting the x-value into the equation of 'f'.
Conclusion on the conditions for H and G to be tangents based on their intersection point relative to the turning point.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: