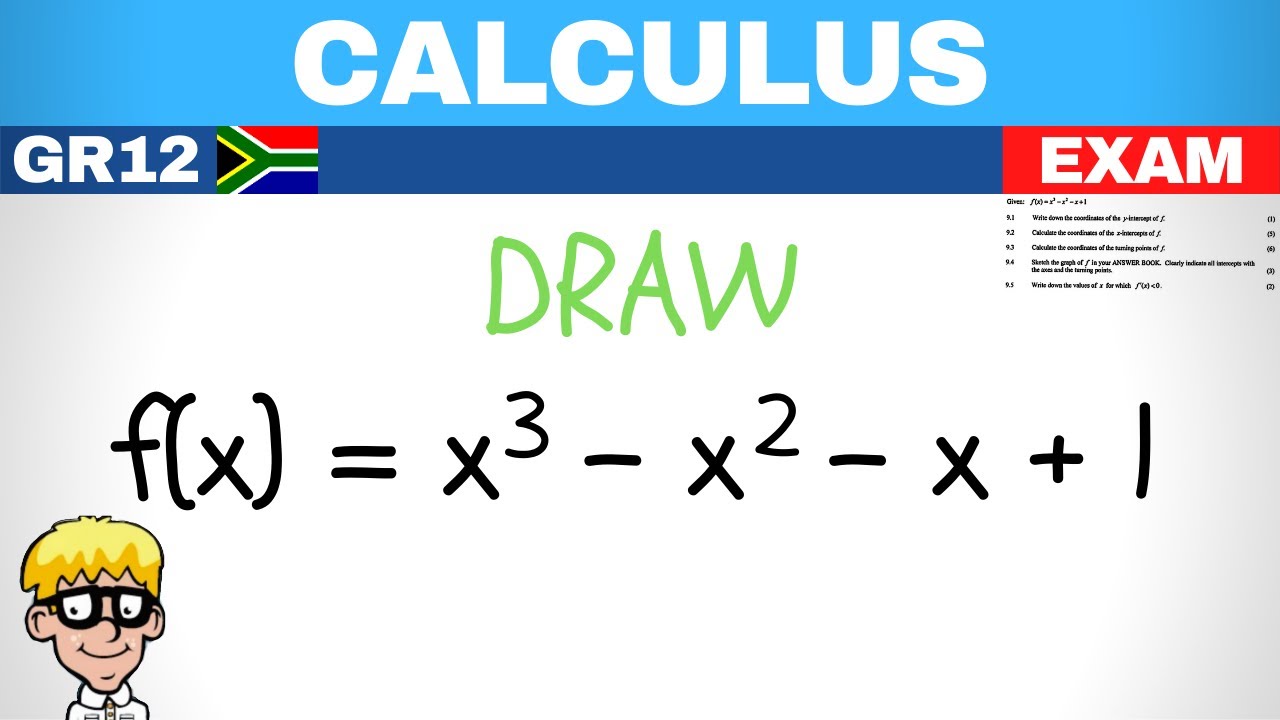Calculus Grade 12: Practice
TLDRThis educational video script discusses the analysis of a cubic function graph, h(x) = ax^3 + bx^2, with a turning point at the origin. It demonstrates how to find the coefficients 'a' and 'b' using given points and derivatives, resulting in a = -1 and b = 6. The script further explains how to determine x-intercepts, intervals of increase, and concavity, and explores the impact of horizontal shifts on the graph. It concludes with determining the range of values for 'k' that result in one negative and two distinct positive roots for the transformed equation.
Takeaways
- 🧮 The problem involves analyzing the graph of a cubic function h(x) = ax^3 + bx^2, with key points at the origin, a turning point at (4, 32), and x-intercepts at specific points.
- 🔍 To solve the problem, plug in the point (4, 32) into the equation to create the first equation: 32 = 64a + 16b, simplifying to 2 = 4a + b.
- 📝 To find turning points, take the first derivative of the cubic function: h'(x) = 3ax^2 + 2bx, and set it to zero to solve for x.
- 🤓 The first derivative at x = 4 is set to zero, leading to a second equation: 0 = 48a + 8b, simplifying to 0 = 6a + b.
- 🔗 With two equations in a and b, solve simultaneously to find a = -1 and b = 6, resulting in the cubic equation h(x) = -x^3 + 6x^2.
- 📍 The x-intercepts are found by setting h(x) = 0, leading to solutions at x = 0 (a double root, indicating a turning point) and x = 6.
- 📈 The graph is increasing where the derivative h'(x) is positive, which occurs between x = 0 and x = 4.
- 🌀 To find where the graph is concave down, take the second derivative h''(x) = -6x + 12 and set it to zero, finding the inflection point at x = 2.
- 🔢 For the cubic function to have one negative and two distinct positive roots, the value of k must lie between 7 and 32, ensuring the graph intersects the line y = k at the desired points.
- ⚙️ The transformation x → x - 1 shifts the graph right by one unit, keeping the y-values unchanged, which is essential in determining the values of k for the specified roots.
Q & A
What is the general form of the cubic function provided in the script?
-The general form of the cubic function is h(x) = ax^3 + bx^2.
How do you find the turning points of a cubic function?
-Turning points of a cubic function are found by taking the first derivative of the function, setting it equal to zero, and solving for the x-values.
What are the given conditions for the cubic function in this problem?
-The cubic function has turning points at the origin (0,0) and another point, with an x-intercept at point A. The coordinates of one point on the graph are provided as (4, 32).
How can you derive the values of 'a' and 'b' in the cubic function?
-To derive the values of 'a' and 'b', you substitute the given point (4, 32) into the function and use the condition that the derivative equals zero at the turning point to create a system of equations. Solving these equations simultaneously gives a = -1 and b = 6.
What does the equation h(x) = -x^3 + 6x^2 represent after finding 'a' and 'b'?
-After finding a = -1 and b = 6, the cubic function h(x) = -x^3 + 6x^2 represents the equation of the graph with the given turning points and x-intercept.
How do you calculate the x-intercept of the cubic function?
-The x-intercept is calculated by setting h(x) = 0 and solving the equation -x^3 + 6x^2 = 0, which can be factored to find the x-values where the graph intersects the x-axis.
What is the significance of the double root at x = 0?
-The double root at x = 0 indicates that there is a turning point at the origin, meaning the graph touches the x-axis at this point but does not cross it.
How can you determine the intervals where the graph is increasing?
-The graph is increasing where the first derivative (h'(x)) is positive. In this case, the graph is increasing on the interval 0 < x < 4.
How do you identify the concave down region of the graph?
-The concave down region is identified by finding where the second derivative (h''(x)) is negative. In this function, the graph is concave down when x > 2.
What is the condition for the graph to have one negative and two distinct positive roots?
-For the graph to have one negative and two distinct positive roots, the value of k must lie between the y-values of the turning points, specifically between 7 and 32.
Outlines
📚 Solving a Cubic Equation with Turning Points
The paragraph discusses a problem involving a cubic equation \( h(x) = ax^3 + bx^2 \) with a turning point at the origin and an x-intercept. The task is to determine the values of 'a' and 'b', given that the graph passes through the point (4, 32). By substituting this point into the equation, an equation in terms of 'a' and 'b' is derived. The turning point is used to find the first derivative and set it to zero, leading to a second equation. Solving these equations simultaneously reveals that \( a = -1 \) and \( b = 6 \). The resulting equation is \( h(x) = -x^3 + 6x^2 \). The x-intercepts are calculated by setting \( h(x) \) to zero, leading to \( x = 0 \) and \( x = 6 \). The paragraph also explains how to determine where the graph is increasing by considering the gradient of the graph.
📉 Analyzing Graph Behavior and Inflection Points
This paragraph continues the mathematical exploration by examining the concavity of the graph and determining the inflection point. The second derivative of the original equation is taken and set to zero to find the x-value of the inflection point, which is found to be 2. The paragraph then addresses the conditions for the graph to have one negative and two distinct positive roots by considering the graph's behavior relative to a horizontal line y=k. The discussion includes examples of different values of 'k' and how they relate to the roots of the equation. The key takeaway is that 'k' must be between the y-values corresponding to the turning points to satisfy the condition of having one negative and two distinct positive roots.
🔍 Determining the Range of 'k' for Specific Root Conditions
The final paragraph focuses on finding the range of values for 'k' that result in the graph having one negative and two distinct positive roots. It explains that 'k' must be between the y-values of the turning points, excluding the y-values themselves, to ensure the roots are distinct and meet the specified conditions. The original graph's y-value at the x-intercept is calculated to be 7, and after a horizontal shift, this value remains the same. The acceptable range for 'k' is thus between 7 and 32, but not including these endpoints, to ensure the graph intersects the line y=k at the correct number of points with the appropriate signs.
Mindmap
Keywords
💡Graph
💡Turning Point
💡X-Intercept
💡First Derivative
💡Second Derivative
💡Cubic Function
💡Inflection Point
💡Concave Down
💡Roots
💡Interval Notation
Highlights
The graph of h(x) = ax^3 + bx^2 has turning points at the origin and at point B.
Given the point (4, 32) on the graph, we can substitute it into the equation to create a system of equations.
Using the first derivative of the cubic function, 3ax^2 + 2bx, and setting it to zero helps find the turning points.
Solving the simultaneous equations derived from the original function and its derivative gives the values of a = -1 and b = 6.
The equation of the graph is then h(x) = -x^3 + 6x^2.
To find the x-intercepts, factorize the equation and solve for x, leading to the intercepts at x = 0 and x = 6.
The graph increases when x is between 0 and 4, where the first derivative is positive.
The concave down portion of the graph is identified using the second derivative and occurs when x > 2.
The graph is concave down where it looks 'sad,' specifically between x = 2 and a point we identify using the second derivative.
A point of inflection occurs at x = 2, where the concavity of the graph changes.
For the graph to have one negative and two distinct positive roots, the value of k must lie between 7 and 32.
When the graph is shifted right by 1 unit, the y-value remains the same, which is crucial for determining k.
If k is equal to 35, the graph only has one negative root.
At k = 10, the graph cuts the x-axis three times, providing one negative and two positive roots.
The correct range for k to satisfy the condition of one negative and two distinct positive roots is 7 < k < 32.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: