Total Internal Reflection and Critical Angle - A Level Physics
TLDRThis script explores the phenomenon of light dispersion and total internal reflection through various shapes, including rectangular, triangular, and semicircular blocks. It explains how white light is split into a spectrum and how light behaves at different interfaces, especially at the critical angle leading to total internal reflection. The script also highlights the practical applications of this principle in optical fibers for communication, demonstrating how signals can be transmitted over long distances with minimal loss, thanks to the refraction and reflection of light.
Takeaways
- 🌈 The script discusses the phenomenon of light dispersion, where white light is split into the colors of the rainbow and possibly infrared light that is not visible to the naked eye.
- 🔭 When light passes through a semicircular block at the correct angle, total internal reflection occurs, causing the light to be reflected within the block instead of passing through.
- 🐠 Total internal reflection is observable in everyday life, such as when looking at a fish tank and seeing fish reflections on the inside.
- 💡 Optical fibers utilize total internal reflection to transmit light signals over long distances, which is the basis for fiber-optic broadband communication.
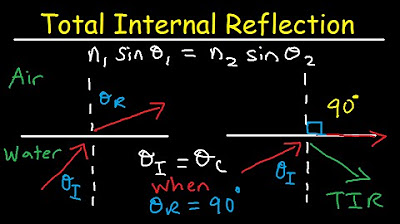
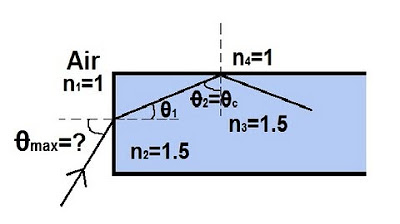
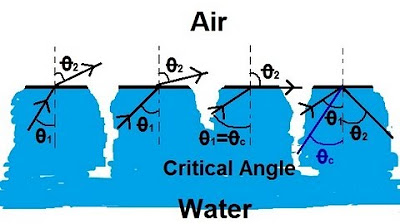
- 📐 The critical angle is defined as the angle of incidence at which the angle of refraction becomes 90°, leading to total internal reflection.
- 🔦 As the angle of incidence increases beyond the critical angle, light is no longer refracted but is instead reflected entirely within the medium.
- 🌟 The script uses a large model of an optical fiber to demonstrate how light travels through and is reflected within the fiber, showing the principle of total internal reflection.
- 🔬 The refractive index is a measure of how much the speed of light slows down when it passes from a vacuum to a different medium, such as air or glass.
- 🔢 The sine of the critical angle (sin C) is equal to the ratio of the refractive index of air (n_air) to that of glass (n_glass), which can be used to calculate the critical angle if the refractive indices are known.
- 🌍 The efficiency of optical fibers in long-distance communication is attributed to their ability to contain a large amount of light, minimizing loss and allowing for near-light-speed signal transmission.
- 🛠️ The script mentions that the curvature of the fiber can affect the amount of light that escapes, with a steeper curvature leading to more light loss due to less effective total internal reflection.
Q & A
What happens when a ray of light passes through a rectangular block?
-When a ray of light passes through a rectangular block, it can be dispersed into the colors of the rainbow, splitting white light into its constituent colors. This phenomenon is due to the different wavelengths of light bending by different amounts as they pass through the material.
What is the significance of a semicircular block in the context of light dispersion?
-A semicircular block is important for studying total internal reflection. If the light hits the curve at the right angle, the angle of incidence can be zero, allowing for the observation of how light behaves as it exits the block, including the point at which total internal reflection occurs.
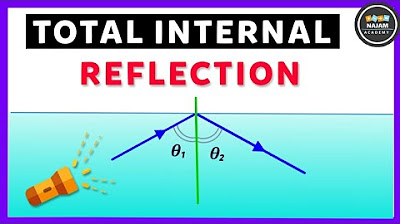
What is total internal reflection and how does it occur?
-Total internal reflection is a phenomenon where light is completely reflected back into the medium it is traveling through, rather than refracting out of it. This happens when the angle of incidence exceeds the critical angle for the medium, causing the light to reflect internally rather than escaping.
How does the angle of refraction compare to the angle of incidence when light passes from a denser to a less dense medium?
-When light passes from a denser medium to a less dense medium, the angle of refraction is always larger than the angle of incidence. This is due to the change in the speed of light as it enters the less dense medium, causing it to bend away from the normal.
What is the critical angle and how is it determined?
-The critical angle is the angle of incidence at which the angle of refraction becomes 90°, causing the light to travel along the boundary between the two media. It is determined by the refractive indices of the two media, being the ratio of the refractive index of the less dense medium to that of the denser medium.
Why is total internal reflection important in optical fibers?
-Total internal reflection is crucial in optical fibers because it allows light to be transmitted over long distances with minimal loss. The light is guided along the fiber by internal reflections, making it ideal for high-speed communication.
What is the role of the refractive index in the context of light dispersion and total internal reflection?
-The refractive index is a measure of how much the speed of light is reduced when it passes from a vacuum into a medium. It plays a key role in determining the bending of light (dispersion) and the critical angle for total internal reflection, which is the sine of the angle of incidence when light passes from one medium to another.
How does the shape of an optical fiber affect the total internal reflection?
-The shape of an optical fiber, particularly the radius of curvature, can affect the efficiency of total internal reflection. A steeper radius of curvature may cause some light to escape, reducing the efficiency of signal transmission.
What is the practical application of total internal reflection in everyday life?
-Total internal reflection has practical applications in various technologies, such as fiber optics for communication, endoscopes in medicine for internal examinations, and prisms in lighting and optical instruments.
How does the dispersion of light in a triangular block differ from that in a rectangular block?
-While the script does not provide specific details on the dispersion in a triangular block, the principle of light dispersion would remain the same as in a rectangular block, with light being split into its constituent colors. The shape of the block might affect the path and distribution of the dispersed light, but the underlying physics would be similar.
Can you provide an example of how total internal reflection is observed in nature?
-An example of total internal reflection observed in nature is the mirage phenomenon. It occurs when light bends while passing through layers of air with different temperatures and densities, creating the illusion of water or reflections on the road.
Outlines
🌈 Light Dispersion and Total Internal Reflection
This paragraph discusses the phenomenon of light passing through different shapes, such as rectangular, triangular, and semicircular blocks, and how it leads to dispersion, splitting white light into a spectrum of colors. The critical concept of total internal reflection is introduced, where light is entirely reflected within the medium at a certain angle, known as the critical angle. This effect is demonstrated using optical fibers, which utilize total internal reflection to transmit light signals over long distances. The paragraph also touches on the practical applications of this principle, such as in fiber optics for broadband communication.
🔢 Understanding the Critical Angle with Refractive Indices
The second paragraph delves into the mathematical relationship between the critical angle and the refractive indices of two media, such as air and glass. It explains how the sine of the critical angle (sin C) is equal to the ratio of the refractive index of air (n_air) to that of glass (n_glass). This relationship allows one to calculate the critical angle if the refractive indices are known. The summary emphasizes the importance of the critical angle in determining whether light will be totally internally reflected or not, which is key to the functionality of optical fibers.
Mindmap
Keywords
💡Rectangular Block
💡Dispersion of Light
💡Semicircular Block
💡Total Internal Reflection
💡Critical Angle
💡Optical Fibers
💡Refraction
💡Refractive Index
💡Infrared
💡Angle of Incidence
💡Angle of Refraction
Highlights
Rectangular block and light dispersion: The explanation of how a rectangular block can disperse white light into the colors of the rainbow.
Infrared and semicircular block: Mention of the presence of infrared light and the significance of a semicircular block in light experiments.
Total internal reflection: The phenomenon where light is completely reflected within a medium, causing no light to exit.
Optical fibers and signal transmission: The practical application of total internal reflection in optical fibers for signal transmission.
Critical angle and its definition: The angle at which the angle of refraction becomes 90°, leading to total internal reflection.
Optical fiber demonstration: A large model of an optical fiber is used to visually demonstrate total internal reflection.
Light loss due to curvature: The impact of the curvature of an optical fiber on light loss and signal attenuation.
Refractive index and its role: The importance of refractive indices in determining the critical angle for total internal reflection.
Calculation of critical angle: The mathematical relationship between the refractive indices of two mediums and the critical angle.
Practical use of optical fibers: The explanation of how optical fibers are used in broadband communication for fast signal transmission.
Dispersion of light in different shapes: The potential for different shapes, such as triangular, to disperse light in various ways.
Angle of incidence and refraction: The relationship between the angle of incidence and the angle of refraction in the context of light passing through different mediums.
Maximization of refraction angle: The point at which the angle of refraction is maximized, leading to total internal reflection.
Reflection within the medium: The observation of light reflecting within the medium instead of exiting, due to total internal reflection.
Optical fiber signal integrity: The discussion on how optical fibers maintain signal integrity over long distances.
Visual demonstration of optical fiber: The use of a torch to visually demonstrate light propagation within a large model of an optical fiber.
Light propagation in optical fibers: The explanation of how light travels through optical fibers and the concept of total internal reflection within.
Transcripts
Browse More Related Video
Total Internal Reflection of Light and Critical Angle of Refraction Physics
Total Internal Reflection and Critical Angle
Refraction & TIR - A-level & GCSE Physics (full version)
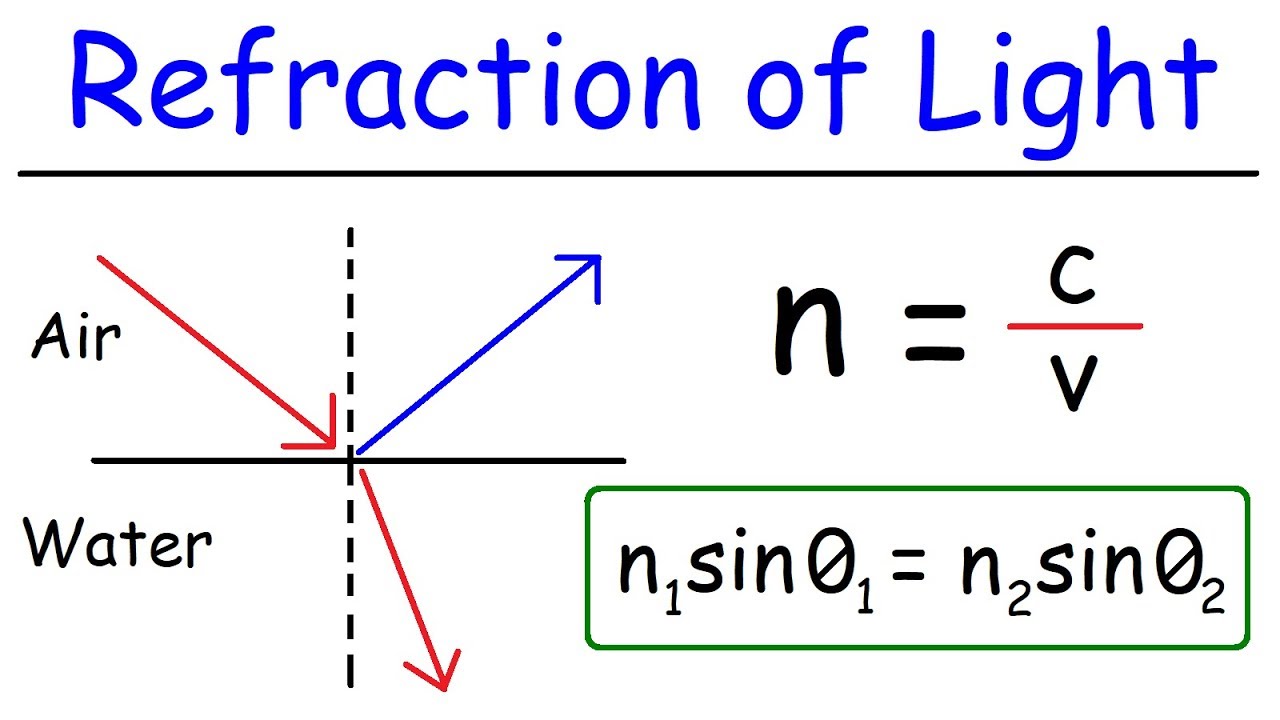
Refraction of Light
Physics 52 Refraction and Snell's Law (5 of 11) The Fiber Optic Cable
Physics 52 Refraction and Snell's Law (4 of 11) Total Internal Reflection: From Water to Air
5.0 / 5 (0 votes)
Thanks for rating: