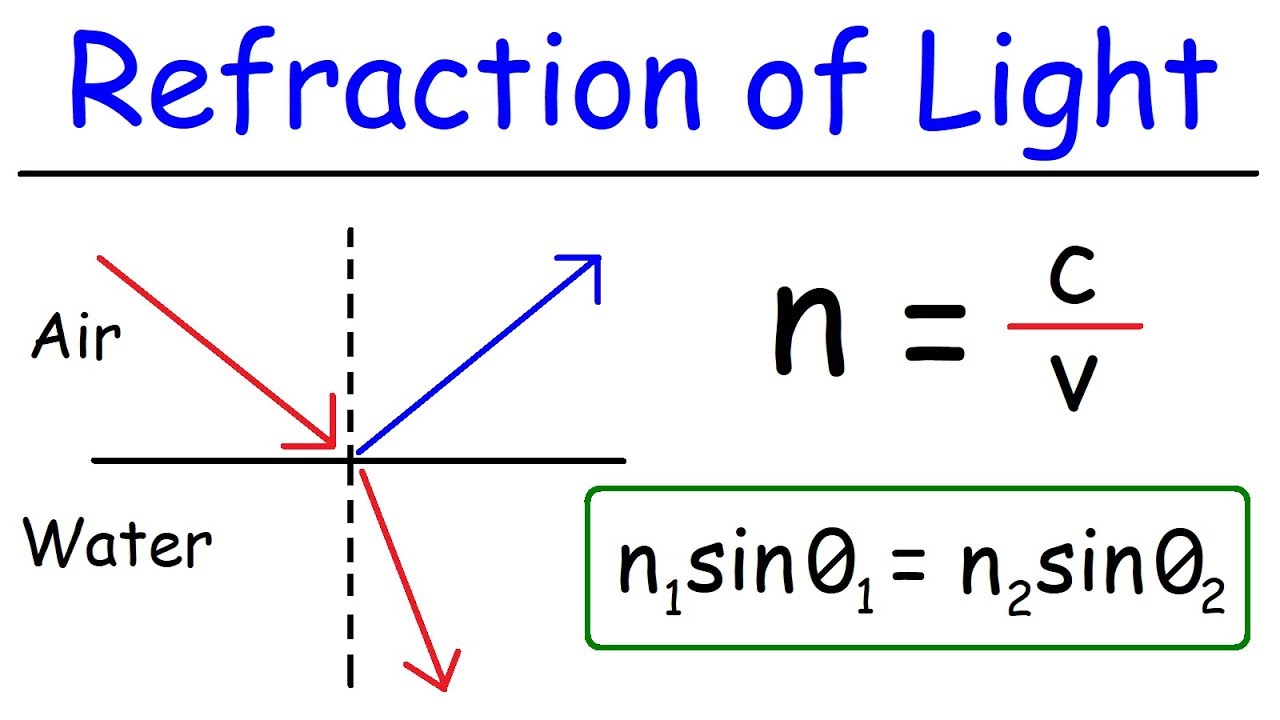Refraction & TIR - A-level & GCSE Physics (full version)
TLDRThe video script discusses the concept of refraction, explaining how the speed of a wave changes when it travels through different media. It clarifies that light, unlike sound, doesn't require a medium and uses the speed of light in a vacuum as a standard. The script delves into the principles of Snell's Law and the refractive index, using practical examples to illustrate how light changes direction when moving between media with different optical densities. It also explores total internal reflection and its application in fiber optic cables, highlighting the technology's ability to transmit multiple signals efficiently and the challenges of dispersion and signal clarity.
Takeaways
- 🌟 Refraction is the change in speed of a wave when it travels from one medium to another, causing a change in direction.
- 🌊 The medium for light is often considered to be space itself, as the concept of 'ether' was dismissed by the Michelson-Morley experiment.
- 💡 The speed of light in a vacuum is approximately 3 x 10^8 meters per second, and it slows down when it travels through other media like water.
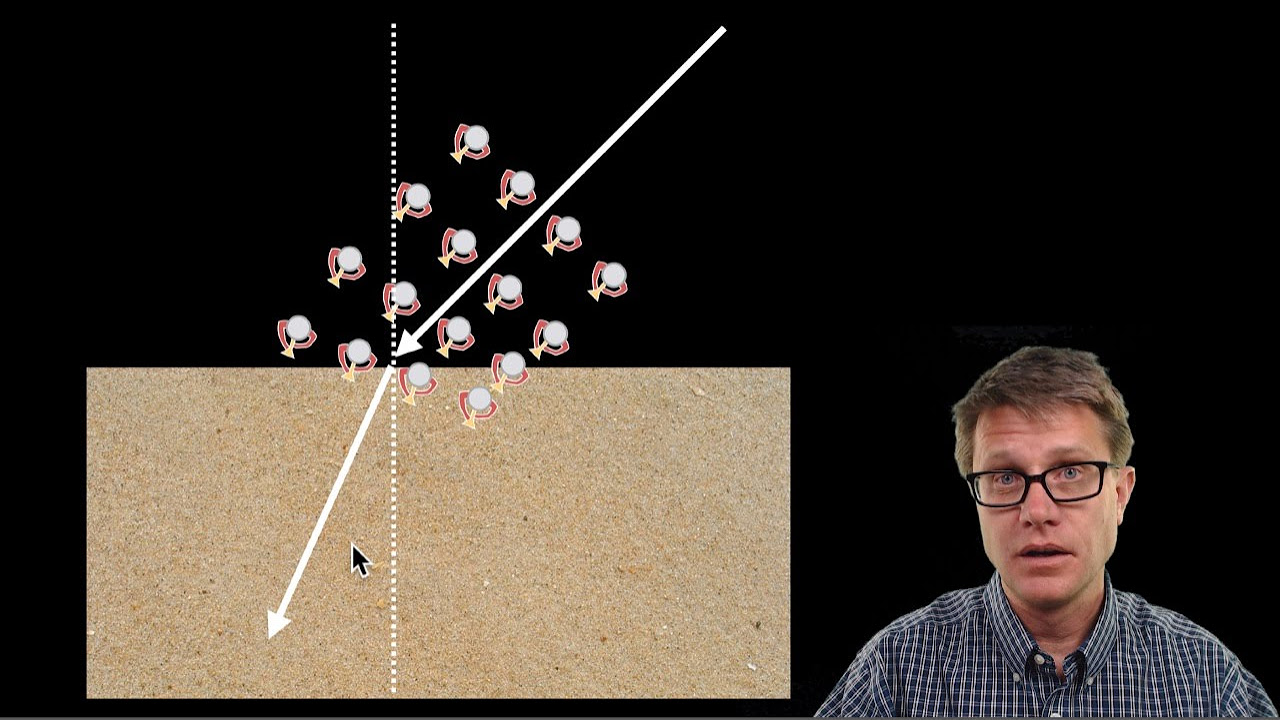
- 📐 When light enters a new medium at an angle, its wavelength shortens and its speed decreases, leading to a change in direction.
- 🔄 The frequency of a wave does not change during refraction, only its speed and wavelength are affected.
- 📐 The refractive index (n) is a ratio that quantifies how much slower light travels in a medium compared to air or vacuum, and is used to predict the degree of refraction.
- 🔄 Snell's Law (n1 sinθ1 = n2 sinθ2) relates the angles of incidence and refraction to the refractive indices of the two media involved.
- 🔍 The critical angle is the angle of incidence at which the angle of refraction becomes 90 degrees, resulting in total internal reflection.
- 🌐 Total internal reflection (TIR) occurs when light attempts to pass from a denser to a less dense medium at an angle greater than the critical angle, and all the light is reflected back.
- 🌐 Fiber optic cables utilize TIR to transmit light signals efficiently over long distances with minimal loss and interference.
- 🌐 Step index fibers are designed with a sudden change in refractive index between the core and cladding to ensure TIR and efficient signal transmission.
Q & A
What is refraction and how does it relate to the medium through which a wave travels?
-Refraction is the change in speed of a wave when it passes from one medium to another, resulting in a change in direction. The medium refers to the substance or space that the wave travels through, such as air, water, or a solid. Refraction occurs because different media have different refractive indices, which quantifies how much slower light travels in a medium compared to a vacuum or air.
What was the historical belief about the medium for light, and what experiment led to its dismissal?
-Historically, it was believed that light traveled through a physical medium called 'ether.' This concept was dismissed after the Michelson-Morley experiment, which provided no evidence for the existence of ether, indicating that light does not require a medium to propagate.
What is the speed of light in a vacuum, and how does it change in air and water?
-The speed of light in a vacuum is approximately 3 x 10^8 meters per second, denoted by the symbol C. In air, the speed of light is very similar to its speed in a vacuum. However, in water, light travels at about 3/4 the speed of its vacuum speed, which is roughly 2.3 x 10^8 meters per second.
Why does the frequency of a wave remain constant during refraction?
-The frequency of a wave remains constant during refraction because it is an intrinsic property of the wave that is determined by the source and is independent of the medium through which the wave is traveling. This constancy is a fundamental principle of wave behavior.
What happens to the wavelength of a wave when it enters a medium with a higher refractive index?
-When a wave enters a medium with a higher refractive index, its speed decreases. Since the frequency remains constant, the wavelength must decrease to maintain the relationship between speed (V), frequency (F), and wavelength (λ) as described by the equation V = λF. This results in the wave's path bending towards the normal to the interface between the two media.
What is the critical angle and how is it related to total internal reflection?
-The critical angle is the angle of incidence at which the angle of refraction becomes 90 degrees, causing the refracted light to travel along the boundary between the two media. Total internal reflection occurs when the angle of incidence exceeds the critical angle, meaning that no light is refracted into the second medium; instead, all the light is reflected back into the first medium.
How does Snell's Law relate to the refractive indices and angles of incidence and refraction?
-Snell's Law states that the ratio of the sine of the angle of incidence (θ1) to the sine of the angle of refraction (θ2) is equal to the ratio of the refractive indices of the two media (n1 and n2). Mathematically, it is expressed as n1 * sin(θ1) = n2 * sin(θ2). This law allows us to calculate the angles of incidence and refraction for a given pair of media and their refractive indices.
What is the significance of the refractive index in the context of fiber optic cables?
-The refractive index is crucial in fiber optic cables because it enables total internal reflection (TIR), which is essential for the efficient transmission of light signals along the cable. A higher refractive index in the core of the fiber optic cable compared to the cladding ensures that light signals are confined within the core and travel without escaping or being refracted into the cladding, leading to minimal signal loss and high transmission quality.
How do fiber optic cables address the issue of multipath dispersion?
-Multipath dispersion, where different light rays take different paths and arrive at the receiver at different times, can be mitigated by making the core of the fiber optic cable as thin as possible, reducing the time difference between the shortest and longest paths. Additionally, installing repeaters or amplifiers along the cable length can help to clean up and regenerate the signal, ensuring that the quality of the transmitted data is maintained.
What is the step index fiber optic cable, and why is it called so?
-A step index fiber optic cable is a type of cable where the refractive index changes abruptly from the core to the cladding. It is called 'step index' because of this sudden change in refractive index, which facilitates total internal reflection (TIR) and helps to keep the light signals confined within the core, resulting in efficient signal transmission.
How does the wavelength of light affect the transmission quality in fiber optic cables?
-In fiber optic cables, different wavelengths of light can be transmitted simultaneously without interfering with each other, a process known as wavelength division multiplexing (WDM). However, different wavelengths may experience slightly different amounts of dispersion, which can affect the transmission quality. To minimize this, the cables are designed to have a specific dispersion profile that ensures all the wavelengths travel at similar speeds, maintaining the integrity of the transmitted signal.
What is the practical application of understanding refraction and total internal reflection in the design of fiber optic communication systems?
-Understanding refraction and total internal reflection is fundamental in the design of fiber optic communication systems because it allows engineers to optimize the properties of the cables to ensure efficient and reliable transmission of light signals. By controlling the refractive indices and dimensions of the core and cladding, designers can achieve total internal reflection and minimize signal loss and dispersion, leading to faster and clearer data transmission.
Outlines
🌟 Understanding Refraction and the Medium for Light
This paragraph introduces the concept of refraction, which is the change in speed of a wave when it travels from one medium to another. It explains that the medium could be a solid, liquid, or gas, and poses the question about the medium for light. The historical notion of 'ether' as a medium for light is discussed and how it was debunked by the Michelson-Morley experiment. The script then explains that the speed of light in a vacuum is represented by the symbol C, and compares this speed to that in air and water. The paragraph also delves into the relationship between the speed of light (V), its frequency (F), and wavelength (lambda), emphasizing that frequency remains constant during refraction, leading to a change in wavelength. A scenario where light transitions from air to water is used to illustrate this concept, highlighting the change in wavelength and velocity.
📐 Exploring the Angle of Incidence and Refractive Index
This section builds upon the concept of refraction by discussing the angle of incidence and the refractive index. It explains that the angle of incidence (theta 1) is the angle at which light strikes the boundary between two media, and the refractive index (n) is a ratio that quantifies how much slower light travels in a medium compared to air. The paragraph introduces the concept of the normal, a line perpendicular to the boundary, which is used to measure the angles of incidence and refraction (theta 2). The refractive index for glass is given as an example, and the implications of a high refractive index are discussed. The paragraph then presents the relationship between the refractive indices of two media and the sine of the angles of incidence and refraction through Snell's Law. It also explains how the refractive index can be determined from the angles using this law and touches upon the concept of total internal reflection (TIR) when light travels from a denser to a less dense medium.
💧 Behavior of Light at the Critical Angle and Total Internal Reflection
This paragraph delves into the behavior of light at the critical angle and the phenomenon of total internal reflection (TIR). It explains that the critical angle is the angle of incidence at which the refracted light aligns with the boundary, and how this is dependent on the refractive indices of the two media. The text describes the transition from refraction to total internal reflection as the angle of incidence increases beyond the critical angle. It emphasizes that TIR occurs when light is in a more dense medium and the angle of incidence exceeds the critical angle. The paragraph also discusses the practical applications of TIR, particularly in fiber optic cables. It explains how TIR allows light to be efficiently transmitted along the cable with minimal loss, and how the design of fiber optic cables with a core, cladding, and protective sheath facilitates TIR. The challenges of multipath dispersion in fiber optics are also mentioned, along with solutions like using thin fibers and installing relays to mitigate this issue.
🌐 Applications of Total Internal Reflection in Fiber Optics
The final paragraph focuses on the real-world application of total internal reflection (TIR) in fiber optics. It explains how TIR enables the efficient transmission of light signals through optic fibers, which are thin strands of glass with a high refractive index core and a lower refractive index cladding. The text discusses the advantages of fiber optic cables, such as the ability to multiplex different wavelengths of light without interference and the speed of information transmission. Challenges like light loss into the cladding and multipath dispersion are also addressed, with the latter being a result of light taking different paths through the cable. To overcome these challenges, the paragraph describes the use of thin fibers and relays that clean and reproduce the signal to prevent signal degradation. The concept of step index fibers is introduced, explaining how the gradual change in refractive index from the core to the cladding ensures TIR and efficient signal transmission. The paragraph concludes by inviting viewers to ask questions or seek clarification in the comments section.
Mindmap
Keywords
💡Refraction
💡Medium
💡Wavelength
💡Frequency
💡Refractive Index
💡Snell's Law
💡Critical Angle
💡Total Internal Reflection
💡Fiber Optic Cables
💡Step Index Optic Fiber
💡Multipath Dispersion
Highlights
Refraction is the change in speed of a wave when it enters a new medium.
The medium for light is space itself, with the speed of light in a vacuum symbolized as C.
The speed of light in water is approximately 3/4 the speed of light in a vacuum.
When the speed of a wave changes, the frequency remains constant, leading to changes in wavelength.
At a 90-degree angle to the boundary (normal), light continues in a straight line with a reduced wavelength.
When light enters at an angle, it refracts, changing direction due to the different speeds in different media.
The refractive index (n) is a ratio that quantifies how much slower light travels in a medium compared to air.
A higher refractive index indicates that light travels slower in the medium, meaning it's more optically dense.
Snell's Law (n1 sinθ1 = n2 sinθ2) describes the relationship between the angles of incidence and refraction.
The critical angle is the angle of incidence that results in the refracted light traveling along the boundary.
Total internal reflection (TIR) occurs when all light is reflected within the denser medium, with no refraction.
For TIR to occur, light must be in the more dense medium and the angle of incidence must be greater than the critical angle.
Fiber optic cables utilize TIR to transmit information quickly, with the core having a higher refractive index than the cladding.
Step index fiber optics have a stepped change in refractive index to ensure TIR and reduce signal degradation.
Multipath dispersion, where different light paths result in signal stretching, can be mitigated by making fibers thin and using relays.
The ability to multiplex different wavelengths in a single fiber optic cable allows for efficient data transmission.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: