Physics 52 Refraction and Snell's Law (4 of 11) Total Internal Reflection: From Water to Air
TLDRThe script delves into the phenomenon of total internal reflection, a fascinating optical property. It explains how light bends when transitioning from a medium with a higher to a lower refractive index, using the example of an underwater observer shining light towards the water's surface. As the angle of incidence increases, the angle of refraction also increases until it reaches 90 degrees, causing the light to skim along the surface. Beyond a critical angle, determined by the refractive indices of the two media, light is completely reflected back into the denser medium, as demonstrated with the critical angle calculation for light traveling from water to air, which is approximately 48.8 degrees.
Takeaways
- 🌟 Total internal reflection is a phenomenon where light is completely reflected back into a medium instead of refracting out of it.
- 💧 This occurs when light travels from a medium with a higher index of refraction to one with a lower index, like from water to air.
- 🔄 Refraction causes light to bend away from the normal when it enters a medium with a lower index of refraction.
- 📏 As the angle of incidence increases, the angle of refraction also increases until it reaches a critical point.
- 🔢 The critical angle is when the angle of refraction is exactly 90 degrees, causing the light to skim along the surface.
- 🚫 Beyond the critical angle, light is no longer refracted but undergoes total internal reflection.
- 🔄 Snell's law (n1 * sin(theta1) = n2 * sin(theta2)) is used to understand the relationship between the angles of incidence and refraction.
- 🔢 To find the critical angle, use the formula: critical angle = arcsin(n2/n1), where n1 and n2 are the indices of refraction of the two media.
- 🌊 In the example given, light traveling from water (n1 = 1.33) to air (n2 = 1) has a critical angle of approximately 48.8 degrees.
- 🔭 At angles greater than the critical angle, light is reflected back into the water as if from a mirror, demonstrating total internal reflection.
- 🌈 This principle is fundamental in various applications, including fiber optics and gemstone brilliance.
Q & A
What is total internal reflection?
-Total internal reflection is a phenomenon where light, when traveling from a medium with a higher index of refraction to one with a lower index, reflects entirely back into the first medium instead of passing through the boundary, when the angle of incidence exceeds a certain threshold known as the critical angle.
Why does light refract when it crosses a boundary?
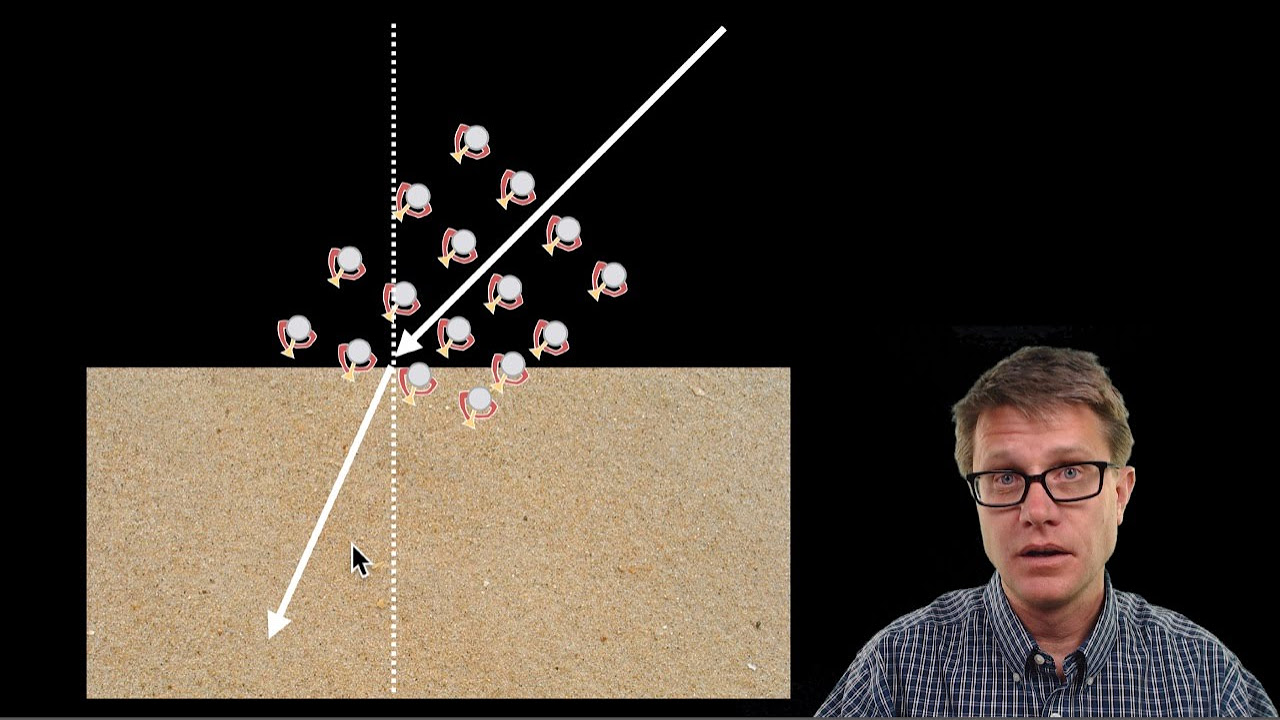
-Light refracts when it crosses a boundary because it changes speed as it passes from one medium to another with a different index of refraction, causing it to bend away from the normal line.
What happens when light travels from water to air?
-When light travels from water to air, it refracts away from the normal because it is moving from a medium with a higher index of refraction (water) to one with a lower index (air).
What is the critical angle?
-The critical angle is the angle of incidence at which the angle of refraction becomes 90 degrees, causing the light to skim along the boundary surface instead of passing through. Beyond this angle, total internal reflection occurs.
How is the critical angle related to the indices of refraction of the two media?
-The critical angle is determined by the ratio of the indices of refraction of the two media. It can be calculated using the formula: critical angle = arcsine(n2/n1), where n1 is the index of refraction of the first medium and n2 is that of the second.
What is the critical angle for light traveling from water to air?
-The critical angle for light traveling from water to air is approximately 48.8 degrees, given that the index of refraction for water is 1.33 and for air is 1.
Why does light skim along the surface when the angle of incidence is at the critical angle?
-When the angle of incidence reaches the critical angle, the angle of refraction becomes 90 degrees, causing the light to travel parallel to the surface, effectively skimming along it.
What occurs when the angle of incidence is greater than the critical angle?
-When the angle of incidence is greater than the critical angle, the light is completely reflected back into the medium with the higher index of refraction, resulting in total internal reflection.
How can total internal reflection be observed underwater with a light beam?
-Total internal reflection can be observed underwater by shining a light beam towards the water's surface from below. If the angle of incidence exceeds the critical angle, the light will reflect off the surface and not escape into the air.
What is Snell's law and how is it used to understand total internal reflection?
-Snell's law relates the angles of incidence and refraction to the indices of refraction of the two media. It is used to calculate the critical angle by setting the angle of refraction to 90 degrees and solving for the angle of incidence at which total internal reflection occurs.
Why is the sine of the critical angle equal to the ratio of the indices of refraction?
-According to Snell's law, when the angle of refraction is 90 degrees, the sine of the critical angle equals the ratio of the second medium's index of refraction to the first, because the sine of 90 degrees is 1, simplifying the equation to sine(critical angle) = n2/n1.
Outlines
🌟 Total Internal Reflection Explained
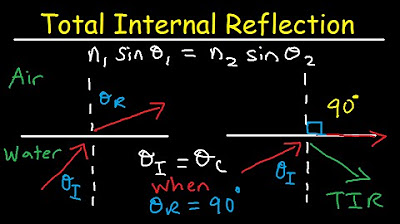
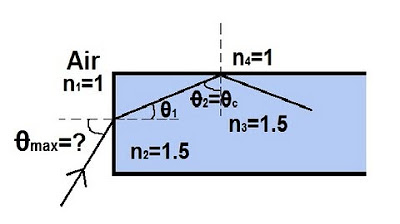
This paragraph introduces the concept of total internal reflection, a phenomenon where light is completely reflected back into a medium instead of refracting into another. It explains the process using the example of a scuba diver shining a light beam from underwater towards the surface. As the angle of incidence increases, the angle of refraction also increases until it reaches 90 degrees, at which point the light skims along the surface. If the angle of incidence is further increased beyond this point, the light no longer exits the medium but reflects back, akin to a mirror. This is known as total internal reflection and depends on the indices of refraction of the two media involved. The critical angle, where refraction becomes 90 degrees, is calculated using Snell's law and is specific to the indices of refraction of the media in question.
Mindmap
Keywords
💡Refraction
💡Total Internal Reflection
💡Critical Angle
💡Index of Refraction
💡Snell's Law
💡Normal
💡Scuba Gear
💡Angle of Incidence
💡Angle of Refraction
💡Arcsine Function
💡Medium
Highlights
Total internal reflection is an interesting property of light refraction when crossing a boundary.
Light bends away from the normal when traveling from a medium with a higher index of refraction to one with a lower index.
As the angle of incidence increases, the angle of refraction also increases.
At a certain critical angle, the angle of refraction becomes 90 degrees, causing the light to skim along the surface.
Beyond the critical angle, light undergoes total internal reflection and no longer leaves the surface.
Total internal reflection depends on the indices of refraction of the two media involved.
The critical angle can be calculated using Snell's law and the indices of refraction.
If the incident angle is greater than the critical angle, total internal reflection occurs.
The critical angle is the angle at which the angle of refraction is 90 degrees.
Snell's law can be rearranged to solve for the critical angle using the formula sin(critical angle) = n2/n1.
The critical angle is found by taking the arcsine of the ratio of the indices of refraction.
For air and water, the critical angle can be calculated using the indices of refraction 1 and 1.33.
The calculated critical angle for air and water is approximately 48.8 degrees.
When the angle of incidence exceeds the critical angle, light will reflect off the surface instead of passing through.
Total internal reflection has practical applications in various optical devices and systems.
Understanding total internal reflection is crucial for designing optical fibers and other light-guiding technologies.
The phenomenon of total internal reflection demonstrates the fascinating behavior of light at the boundary between two media.
Transcripts
Browse More Related Video

Total internal reflection | Geometric optics | Physics | Khan Academy
Total Internal Reflection of Light and Critical Angle of Refraction Physics
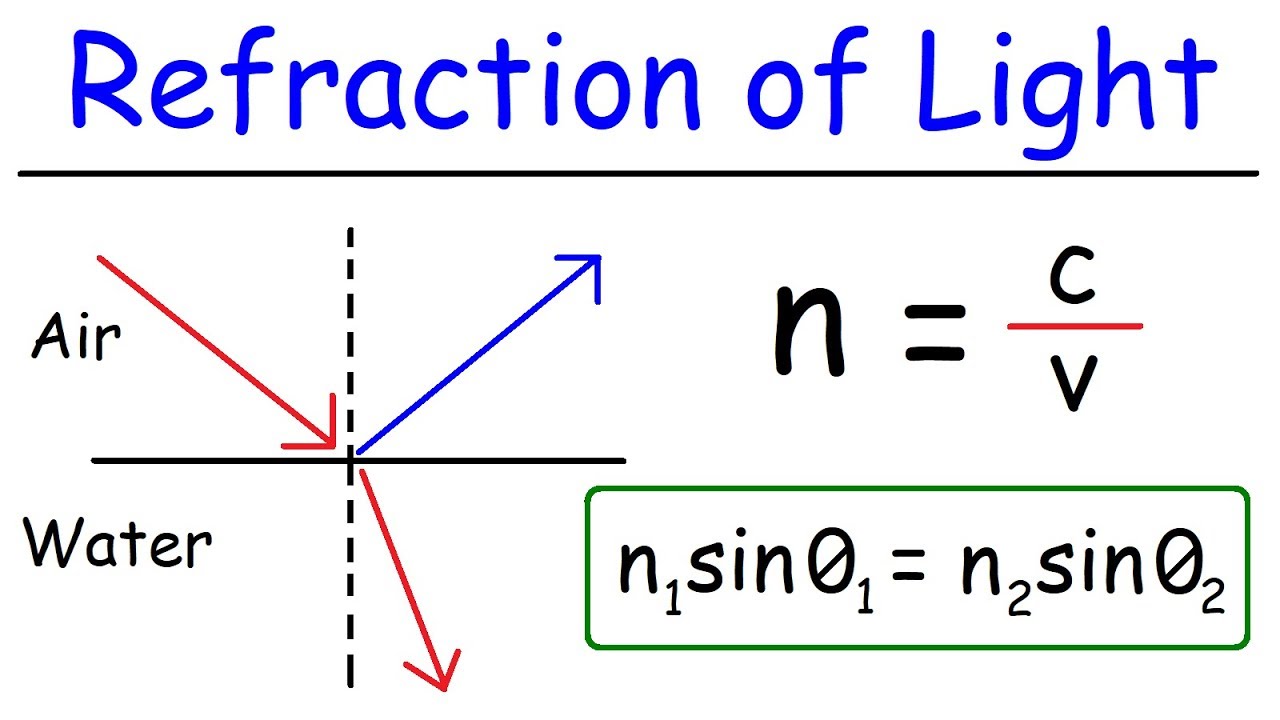
Refraction of Light
Physics 53 Polarization (5 of 5) Brewster's Angle
Refraction of Light
Physics 52 Refraction and Snell's Law (5 of 11) The Fiber Optic Cable
5.0 / 5 (0 votes)
Thanks for rating: