Total Internal Reflection of Light and Critical Angle of Refraction Physics
TLDRThis educational video explores the phenomenon of total internal reflection and the calculation of the critical angle. It explains how light behaves when transitioning between materials with different indices of refraction, such as air and water, or water and diamond. The video demonstrates that total internal reflection occurs when light moves from a material with a higher index to one with a lower index, and provides the formula for calculating the critical angle using Snell's law. Examples are given to illustrate the concept, including calculating the critical angle for the interface between glass and water, and determining the index of refraction of an unknown solid based on its critical angle with air.
Takeaways
- 🌟 Total internal reflection (TIR) occurs when light travels from a medium with a higher index of refraction to one with a lower index of refraction.
- 🔍 The critical angle is the angle of incidence at which the angle of refraction becomes 90 degrees, leading to TIR.
- 📐 Snell's Law, n_1 * sin(theta_1) = n_2 * sin(theta_2), is used to describe the relationship between the angles of incidence and refraction.
- 🌊 The index of refraction for air is approximately 1, and for water, it is 1.33.
- 💎 Diamond has a much higher index of refraction compared to air, at about 2.42, causing light to bend towards the normal line when traveling from water to diamond.
- 📉 As the index of refraction increases, the angle of refraction decreases when light travels from a denser to a less dense medium.
- 🚫 TIR will not occur between water and diamond because light is traveling from a less dense to a denser medium.
- 🔄 When the angle of incidence exceeds the critical angle, refraction no longer occurs, and only reflection happens, resulting in TIR.
- 📚 To calculate the critical angle, use the formula sin(theta_c) = 1 / n, where n is the index of refraction of the denser medium.
- 📈 The critical angle for the interface between air and water is approximately 48.75 degrees, as calculated using the index of refraction for water.
- 💡 The critical angle for the interface between a solid and air can be determined if the angle is known, as shown in the example with a 40-degree critical angle leading to an index of refraction of 1.56 for the solid.
Q & A
What is total internal reflection?
-Total internal reflection is a phenomenon where light traveling from a medium with a higher index of refraction to one with a lower index of refraction is completely reflected back into the first medium when the angle of incidence exceeds the critical angle, with no refraction occurring.
What is the critical angle and how is it related to total internal reflection?
-The critical angle is the angle of incidence at which the angle of refraction becomes 90 degrees. When the incident angle exceeds the critical angle, total internal reflection occurs because the light is no longer refracted but entirely reflected back into the medium with the higher index of refraction.
What is the law of reflection?
-The law of reflection states that the angle of incidence is equal to the angle of reflection (Theta I = Theta R). This law describes how light reflects off a surface, with the incident ray and the reflected ray forming equal angles with the normal to the surface.
What is Snell's law and how does it relate to the angles of incidence and refraction?
-Snell's law is the equation N1 sin(Theta1) = N2 sin(Theta2) that relates the angles of incidence (Theta1) and refraction (Theta2) to the indices of refraction (N1 and N2) of the two media involved. It explains how light bends when it passes from one medium to another.
What is the index of refraction and how does it affect the direction of light?
-The index of refraction is a measure of how much light slows down and bends when it enters a medium from a vacuum or another medium. A higher index of refraction means light will bend more towards the normal when moving from a medium with a higher index to one with a lower index, and vice versa.
Why does light bend away from the normal line when it travels from water to air?
-Light bends away from the normal line when traveling from water to air because air has a lower index of refraction than water. According to Snell's law, this causes the angle of refraction to be greater than the angle of incidence, resulting in the bending away from the normal.
How can you calculate the critical angle for a medium with an index of refraction of 1.33?
-To calculate the critical angle for a medium with an index of refraction (N) of 1.33, you would use the formula for the critical angle which is the inverse sine of the reciprocal of the index of refraction (sin^-1(1/N)). In this case, it would be sin^-1(1/1.33), which gives an approximate critical angle of 48.75 degrees.
What happens if the incident angle exceeds the critical angle?
-If the incident angle exceeds the critical angle, refraction no longer occurs because the sine of the angle of refraction would exceed 1, which is not possible. Instead, the light is completely reflected back into the medium with the higher index of refraction, resulting in total internal reflection.
Why is it not possible for total internal reflection to occur from water to diamond?
-Total internal reflection cannot occur from water to diamond because diamond has a higher index of refraction than water. Total internal reflection only happens when light travels from a medium with a higher index of refraction to one with a lower index of refraction, not the other way around.
How can you determine the index of refraction of a solid if the critical angle between the solid and air is 40°?
-If the critical angle between a solid and air is 40°, you can determine the index of refraction of the solid using Snell's law with the formula N2 = (sin 90) / (sin 40°). Since sin 90 is 1, the index of refraction of the solid would be approximately 1.56.
Outlines
🌟 Total Internal Reflection and Critical Angle Basics
This paragraph introduces the concept of total internal reflection and the critical angle. It explains the phenomenon of light striking the boundary between two materials, such as air and water, and the resulting behaviors of reflection and refraction. The law of reflection and Snell's law are discussed to describe how the angle of incidence relates to the angle of refraction. The paragraph emphasizes that total internal reflection occurs when light travels from a material with a higher index of refraction to one with a lower index, and it highlights the importance of the angle of incidence in relation to the normal line.
🔍 Calculating the Critical Angle and Total Internal Reflection
The second paragraph delves into the calculation of the critical angle, which is the angle of incidence at which the angle of refraction becomes 90 degrees. It explains that beyond this angle, total internal reflection takes place because there is no longer any refraction. The paragraph provides an example calculation using Snell's law for air and water, demonstrating how to find the critical angle by setting the refracted angle to 90 degrees and solving for the incident angle. It also illustrates the impossibility of refraction when the incident angle exceeds the critical angle, leading to a situation where reflection is the only outcome.
📚 Practice Problems and Determining the Index of Refraction
The final paragraph presents practice problems to calculate the critical angle between different materials, such as glass and water, and to determine the index of refraction of an unknown solid. It reinforces the concept that the critical angle is associated with the lower index of refraction and that light must travel from a higher to a lower index of refraction for total internal reflection to occur. The paragraph guides through the process of using Snell's law to find the critical angle for the glass-water interface and to solve for the index of refraction of a solid when given the critical angle for the solid-air interface.
Mindmap
Keywords
💡Total Internal Reflection
💡Critical Angle
💡Index of Refraction
💡Incident Angle
💡Reflected Ray
💡Refracted Ray
💡Snell's Law
💡Normal Line
💡Reflection
💡Refraction
Highlights
Introduction to the concept of total internal reflection and the calculation of the critical angle.
Explanation of the boundary between two materials with air on top and water on the bottom.
Definition of the normal line, incident ray, and incident angle.
Description of reflection and the law of reflection where the angle of incidence equals the angle of reflection.
Introduction of Snell's law and its relation between the angle of incidence and the angle of refraction.
Explanation of how light bends when traveling from a material with a high index of refraction to one with a low index.
Condition for total internal reflection to occur: light must travel from a high to a low index of refraction.
Demonstration of how increasing the incident angle leads to the critical angle and total internal reflection.
Calculation of the critical angle using Snell's law with the indices of refraction for air and water.
The critical angle is when the refracted angle is 90 degrees, and the incident angle exceeds this point.
Example calculation of the critical angle between air and water, resulting in approximately 48.75 degrees.
Illustration of the impossibility of refraction when the incident angle exceeds the critical angle, leading to total internal reflection.
Practice problem: calculating the critical angle between glass and water using their respective indices of refraction.
Explanation of the critical angle for the interface between a solid and air being 40° and how to calculate the solid's index of refraction.
Final summary of the process for calculating the critical angle and the conditions necessary for total internal reflection.
Conclusion and thanks for watching, highlighting the educational value of the video.
Transcripts
Browse More Related Video
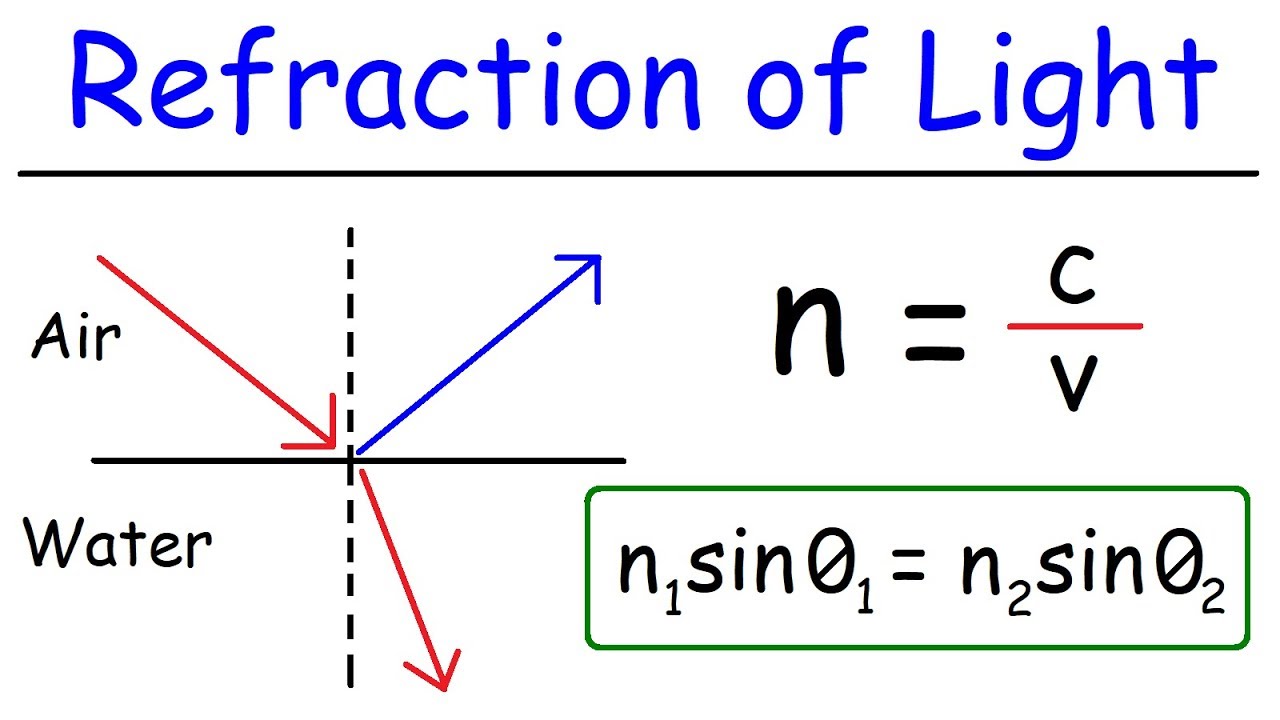
Refraction of Light
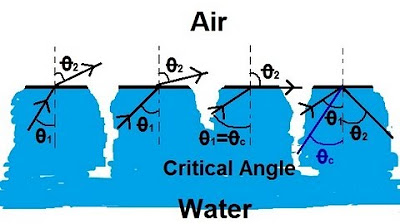
Physics 52 Refraction and Snell's Law (4 of 11) Total Internal Reflection: From Water to Air

Snell's Law & Index of Refraction Practice Problems - Physics

Total internal reflection | Geometric optics | Physics | Khan Academy
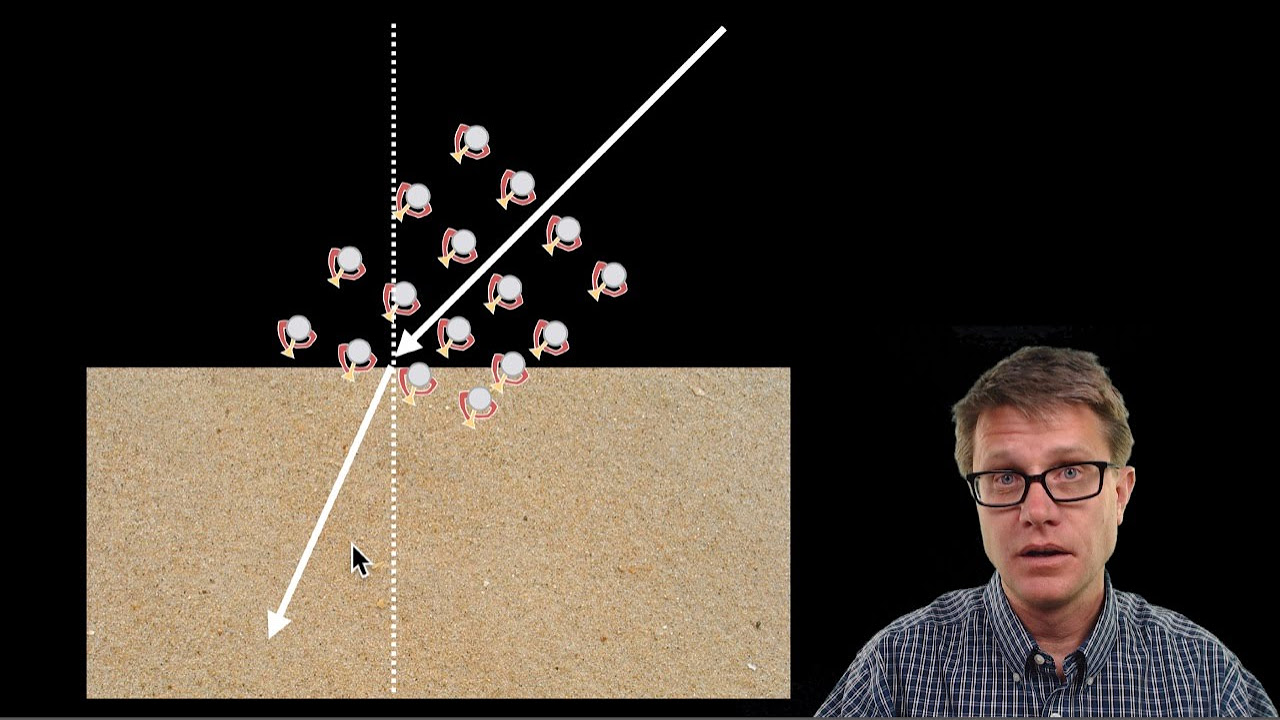
Refraction of Light
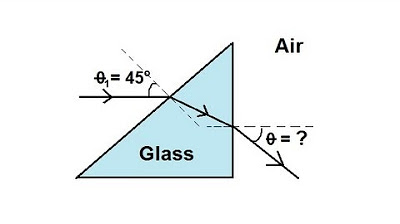
Physics 52 Refraction and Snell's Law (3 of 11) Light Ray Through A Prism
5.0 / 5 (0 votes)
Thanks for rating: