Physics 52 Refraction and Snell's Law (5 of 11) The Fiber Optic Cable
TLDRThis lecture explores the phenomenon of total internal reflection in fiber-optic cables, crucial for long-distance communication. It explains how light pulses are guided through these glass cables without escaping, by ensuring the angle of incidence is greater than the critical angle, calculated using Snell's law. The critical angle for a typical cable is 41.8 degrees, and surprisingly, there's no upper limit for the angle of incidence, as the light will always remain within the cable, demonstrating an intriguing aspect of fiber-optic technology.
Takeaways
- 🌟 Total internal reflection is a principle used in fiber-optic cables to transmit messages over long distances with light pulses.
- 🔍 Fiber-optic cables are made of glass and are used for communication in buildings and across oceans.
- 📐 The critical angle is essential for total internal reflection to occur within the fiber-optic cable, ensuring light does not escape.
- 🔄 When light enters the fiber-optic cable at an angle, it is totally internally reflected back into the cable if the angle of incidence is at least the critical angle.
- 💡 The lecture discusses the scenario where light enters the fiber-optic cable perpendicularly and seeks to determine the largest possible angle for total internal reflection.
- 📚 Snell's law is used to calculate the critical angle for total internal reflection, given the refractive indices of the materials involved.
- 🔢 The refractive index of the fiber-optic cable is given as 1.5, and calculations are based on this value.
- 🧭 The critical angle is calculated to be 41.8 degrees using the formula: critical angle = arcsine(n4/n3), where n3 is the refractive index of the cable and n4 is that of air (1).
- 📐 The angle of incidence (theta sub 1) can be varied, but the angle of refraction (theta sub 2) must be less than or equal to 48.2 degrees to maintain total internal reflection.
- 🔄 Regardless of the angle of incidence, as long as it is within the limits, the light will continue to propagate within the fiber-optic cable without escaping.
- 🔬 The lecture concludes that there is no maximum angle for the incidence of light into the fiber-optic cable, as long as it is less than 90 degrees, ensuring continuous transmission.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the principle of total internal reflection and its application in fiber-optic cables for long-distance communication.
What is a fiber-optic cable?
-A fiber-optic cable is a cable made of glass or plastic that transmits light signals for communication purposes, used in buildings, across oceans, and other locations.
How does total internal reflection work in fiber-optic cables?
-Total internal reflection occurs when a light beam is shone into the fiber-optic cable at an angle such that when it hits the sides of the cable, it is reflected back into the cable instead of exiting.
What is the critical angle in the context of fiber-optic cables?
-The critical angle is the minimum angle of incidence at which light must enter the fiber-optic cable to ensure total internal reflection, preventing the light from leaving the cable.
What is the index of refraction of the fiber-optic cable mentioned in the script?
-The index of refraction of the fiber-optic cable mentioned in the script is 1.5.
How is Snell's law used to determine the critical angle for total internal reflection?
-Snell's law is used to equate the ratio of the sine of the angles of incidence and refraction to the ratio of the indices of refraction of the two media. For total internal reflection, the critical angle is found by setting the refracted angle to 90 degrees and solving for the incident angle.
What is the calculated critical angle for a fiber-optic cable with an index of refraction of 1.5?
-The calculated critical angle for a fiber-optic cable with an index of refraction of 1.5 is 41.8 degrees.
What is the relationship between theta sub 3 and theta sub 2 in the context of the lecture?
-Theta sub 3 is the angle of incidence inside the fiber-optic cable, and theta sub 2 is the angle of refraction. They are related such that theta sub 3 must be at least 41.8 degrees, and theta sub 2 must be less than or equal to 48.2 degrees to ensure total internal reflection.
What is the maximum angle of incidence (theta sub 1) that can be used for light entering the fiber-optic cable?
-There is no maximum angle of incidence for light entering the fiber-optic cable. Any angle of incidence will result in total internal reflection as long as theta sub 2 remains less than or equal to 48.2 degrees.
What happens when the angle of incidence (theta sub 1) is made as large as possible, equal to 90 degrees?
-When theta sub 1 is made equal to 90 degrees, the largest possible value for theta sub 2 is 41.8 degrees, which confirms that total internal reflection will occur regardless of the angle of incidence as long as the conditions for total internal reflection are met.
Outlines
🌟 Total Internal Reflection in Fiber-Optic Cables
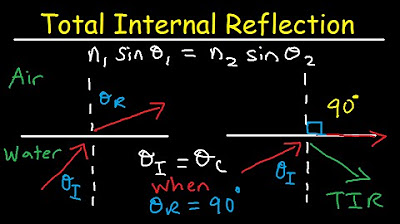
This paragraph introduces the concept of total internal reflection and its application in fiber-optic cables for long-distance communication. It explains how light pulses are transmitted through a glass cable by being totally internally reflected at the cable's sides, ensuring they do not escape. The critical angle is discussed, which is the minimum angle of incidence required for light to be reflected without refracting out of the cable. The paragraph also explores a scenario where light enters the cable perpendicularly and calculates the largest possible angle for total internal reflection to occur, using Snell's law and the refractive index of the cable, which is 1.5. The critical angle is determined to be 41.8 degrees, meaning any angle of incidence greater than this will result in total internal reflection.
🔍 Theoretical Exploration of Light Incidence Angles in Fiber Optics
The second paragraph delves deeper into the theoretical aspects of light incidence in fiber-optic cables. It discusses the possibility of increasing the angle of incidence to its extreme, questioning whether there is a limit to how large this angle can be while still maintaining total internal reflection. Through calculations using Snell's law, it is revealed that the angle of incidence can be as large as desired without affecting the critical angle for total internal reflection, which remains at 41.8 degrees. The paragraph concludes with an interesting finding that there is no maximum angle for theta sub one, as the light will continue to propagate within the cable regardless of the angle, as long as it is greater than the critical angle. This result challenges initial expectations and provides a deeper understanding of the physics involved in fiber-optic communication.
Mindmap
Keywords
💡Total Internal Reflection
💡Fiber-Optic Cable
💡Critical Angle
💡Index of Refraction
💡Snell's Law
💡Angle of Incidence
💡Angle of Refraction
💡Light Pulses
💡Communication
💡Arc Sine
Highlights
Total internal reflection is used in fiber-optic cables to transmit light pulses for communication over long distances.
Fiber-optic cables are made of glass and are used in buildings and across oceans for communication.
Light beams in a fiber-optic cable are totally internally reflected back into the cable if they hit the sides at the right angle.
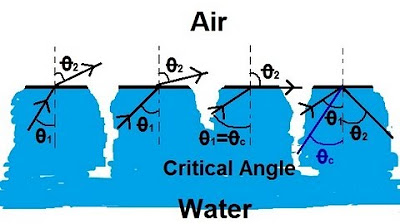
The critical angle for total internal reflection in a fiber-optic cable is when the refracted angle equals 90 degrees.
Snell's law is used to calculate the critical angle for total internal reflection in a fiber-optic cable.
The index of refraction of a fiber-optic cable is typically 1.5.
The critical angle is calculated using the formula: critical angle = arc sine (n4/n3).
For a typical fiber-optic cable, the critical angle is 41.8 degrees.
The angle of incidence (theta sub 3) should be at least 41.8 degrees to ensure total internal reflection.
The angle of refraction (theta sub 2) is calculated using Snell's law and is less than or equal to 48.2 degrees.
The angle of incidence (theta sub 1) can be any size as long as it is perpendicular to the cable.
No matter how large the angle of incidence, the light will never leave the fiber-optic cable if theta sub 2 is less than 48.2 degrees.
The maximum angle of refraction (theta sub 2) is 41.8 degrees when the angle of incidence (theta sub 1) is 90 degrees.
The light will continue to propagate through the fiber-optic cable regardless of the angle of incidence as long as it meets the conditions for total internal reflection.
This demonstrates the unique properties of fiber-optic cables and their ability to transmit light efficiently over long distances.
Transcripts
Browse More Related Video

Total internal reflection | Geometric optics | Physics | Khan Academy
Total Internal Reflection of Light and Critical Angle of Refraction Physics
Physics 52 Refraction and Snell's Law (4 of 11) Total Internal Reflection: From Water to Air
Refraction of Light
Physics 51 - Optics: Reflections (2 of 2) Inbound and Exit Ray
Geometric Optics 2
5.0 / 5 (0 votes)
Thanks for rating: