Unit VI: Lec 4 | MIT Calculus Revisited: Single Variable Calculus
TLDRThis MIT OpenCourseWare lecture delves into improper integrals, a fundamental concept in calculus. Professor Herbert Gross introduces the topic with a riddle, highlighting the pitfalls of misapplication of the first fundamental theorem. He explains two types of improper integrals: those with infinite integrands over finite intervals and those with finite integrands over infinite intervals. Through examples, he illustrates the process of evaluating these integrals, emphasizing the importance of understanding the behavior of functions at infinity and cautioning against the oversight that can lead to incorrect conclusions.
Takeaways
- 📚 The lecture introduces the concept of improper integrals, which are integrals with limits of integration that are infinite or where the integrand is infinite at some point within the interval.
- 🔍 The 'find the flaw' riddle highlights a common mistake in calculating improper integrals, showing that the integral of 1/x^2 from -1 to 1 should not yield a negative result, as the area under the curve should be positive.
- 📉 The importance of the first fundamental theorem of calculus is emphasized, but with a caveat that it requires the function to be piecewise continuous on the interval of integration.
- 🚫 The concept of infinity in improper integrals is addressed, noting that the integral becomes improper if the function is infinite at a point within the integration limits.
- 🔄 The definition of improper integrals is given, distinguishing between two types: those where the integrand is infinite (first kind) and those where the limits of integration are infinite (second kind).
- 📝 A method to handle improper integrals is presented, which involves working around the point of infinity by taking limits as the problematic point is approached.
- 📉 The script uses the example of the integral of 1/x from 0 to 1 to illustrate the process of evaluating an improper integral and the concept of convergence.
- 📏 The difference between horizontal and vertical strip methods in calculating area under a curve is discussed, showing how changing the method can lead to different types of improper integrals.
- 🌐 The relationship between improper integrals of the first and second kind is highlighted, showing that they are closely connected and can be transformed into each other.
- 📊 The script provides examples of volumes of revolution, demonstrating how an infinite area can enclose a finite volume when rotated around an axis.
- ⚠️ A warning is given about the dangers of improper integrals of the first kind, where the integrand may become infinite, and the importance of checking for this before proceeding with integration.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is improper integrals, which are integrals that involve unbounded integrands or extend to infinity.
What is the first example given in the lecture to illustrate the concept of improper integrals?
-The first example given is the integral of '1/x^2' from -1 to 1, which is calculated incorrectly as -2, highlighting the need to find the flaw in the calculation.
Why is the result of the integral from -1 to 1 of '1/x^2' being -2 considered preposterous?
-The result is considered preposterous because the integrand '1/x^2' is non-negative over the interval, and the integral should represent a sum of positive areas, which cannot be negative.
What is the fundamental theorem of calculus that is incorrectly applied in the first example?
-The first fundamental theorem of calculus, which states that the integral from 'a' to 'b' of 'f(x) dx' is 'F(b) - F(a)' where F'(x) = f(x), is incorrectly applied without considering the discontinuity at x=0.
What is the definition of an improper integral of the first kind?
-An improper integral of the first kind is defined as an integral where the integrand is infinite for at least one point 'c' in the interval from 'a' to 'b'.
How is the improper integral of the first kind calculated?
-The improper integral of the first kind is calculated by working around the point of infinity, using the limit as 'h' approaches 0 of the integral from 'a' to 'c-h' plus the integral from 'c+h' to 'b'.
What is the definition of an improper integral of the second kind?
-An improper integral of the second kind is defined as an integral where the limits of integration are infinite, even though the integrand is finite over the entire range.
What is the difference between an improper integral of the first kind and an improper integral of the second kind?
-The difference lies in whether the issue is with the integrand becoming infinite (first kind) or the limits of integration being infinite (second kind).
How can the area under a curve be determined when the integrand is infinite at a point within the interval?
-The area can be determined by considering the limit as 'h' approaches 0 of the integral over the interval excluding a small interval around the point of infinity, effectively 'squeezing' the area around the infinite point.
What is the significance of the example involving '1/x' as the integrand from 1 to infinity?
-The example with '1/x' from 1 to infinity is significant because it demonstrates that an infinite area can generate a finite volume when rotated about the x-axis, highlighting the peculiarities of improper integrals.
Why is it not necessary to compute the exact limit to determine if an improper integral is convergent?
-It is not necessary because if the improper integral is bounded by another integral that is known to be convergent, it can be inferred that the original integral is also convergent, even without knowing the exact limit.
What is the final advice given regarding the handling of improper integrals?
-The final advice is to be cautious with improper integrals, especially of the first kind, as mathematics does not have built-in alarms for errors. It is important to check for infinite values of the integrand within the interval of integration.
Outlines
📚 Introduction to Improper Integrals
The video script begins with an introduction to improper integrals, highlighting the importance of the Creative Commons license in supporting MIT OpenCourseWare. The lecturer, Herbert Gross, presents a calculus riddle involving the integral of '1/x^2' from -1 to 1, which seemingly results in a negative value, contradicting the expected positive area. This contradiction is used to emphasize the need for caution when dealing with improper integrals and to introduce the concept of areas represented by non-negative integrands. The flaw in the initial calculation is pointed out, noting that the first fundamental theorem of calculus requires the integrand to be piecewise continuous, which is not the case when the integrand approaches infinity, as it does at x=0 in this example.
🔍 Definition and Handling of Improper Integrals
The second paragraph delves into the definition of improper integrals, distinguishing between the two types: those with infinite integrands over a finite interval (Type 1) and those with finite integrands over an infinite interval (Type 2). The lecturer explains how to handle Type 1 improper integrals by working around the point of infinity, using limits to evaluate the integral on either side of the discontinuity. The concept of area under a curve is used to provide a geometric interpretation of these integrals, and the importance of the rate at which 'h' approaches zero compared to the integrand approaching infinity is discussed.
📉 Convergence and Divergence of Improper Integrals
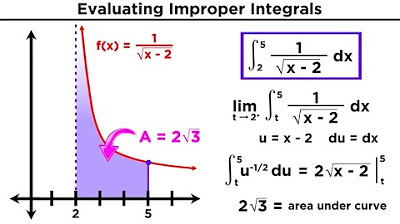
In the third paragraph, the script discusses the convergence and divergence of improper integrals. It explains that a convergent integral is one where the limit exists and is finite, while a divergent integral has a limit that is infinite. The lecturer provides examples to illustrate this, including the integral of '1/sqrt(x)' from 0 to 1, which is convergent with a finite area of 2, contrasting with the earlier divergent example. The paragraph emphasizes the subtlety and importance of the behavior of the function near points of discontinuity.
🌐 Volumes of Revolution and the Indeterminate Forms of Infinity
The fourth paragraph explores the concept of volumes of revolution, demonstrating how regions with infinite areas can generate finite volumes when rotated around an axis. The lecturer uses the example of rotating the region bounded by '1/x' around the x-axis, resulting in a finite volume despite the infinite area of the region. This highlights the indeterminate forms that can arise with improper integrals and the need for careful consideration of the rate at which functions approach zero or infinity.
📘 Comparison of Improper Integrals of the First and Second Kinds
The fifth paragraph compares and contrasts the two types of improper integrals, showing how they are structurally different but closely connected. The lecturer illustrates this by inverting the role of x and y in the integral, effectively transforming a Type 1 improper integral into a Type 2 by changing the orientation of the integration strips. The paragraph emphasizes the importance of understanding the behavior of the integrand and the limits of integration when evaluating improper integrals.
🚀 Conclusion and Cautionary Advice on Improper Integrals
In the final paragraph, the lecturer concludes the discussion on improper integrals by summarizing the key points and offering cautionary advice. The script emphasizes the importance of recognizing when an integral is improper and the potential pitfalls of overlooking the conditions required for the application of the first fundamental theorem of calculus. The lecturer reminds viewers that while improper integrals of the second kind can be complex to evaluate, they are not inherently dangerous, but improper integrals of the first kind require extra vigilance to avoid incorrect calculations.
Mindmap
Keywords
💡Improper Integrals
💡First Fundamental Theorem of Integral Calculus
💡Convergence
💡Divergence
💡Continuity
💡Limits of Integration
💡Infinite Discontinuity
💡Piecewise Continuous
💡Volume of Revolution
💡Indeterminate Forms
💡Inverse Functions
Highlights
Introduction to improper integrals and the concept of finding the flaw in a mathematical riddle.
The importance of the first fundamental theorem of integral calculus and its limitations when dealing with improper integrals.
The incorrect calculation of the integral from -1 to 1 of '1/x^2' leading to a paradoxical result.
The visualization of improper integrals as areas under a curve and the expectation of a positive result.
The definition of improper integrals and the conditions under which they occur.
The distinction between improper integrals of the first and second kind based on the nature of infinity involved.
The method to handle improper integrals by working around the point of infinity using limits.
The interpretation of improper integrals in terms of area calculation and the significance of infinite regions.
The problem of determining the area of an infinite region and the concept of infinity times zero.
The evaluation of improper integrals using finite cases and the process of taking limits.
The comparison between different improper integrals and their convergence or divergence.
The concept of volumes of revolution and how they relate to improper integrals and infinite regions.
The surprising result that an infinite area can enclose a finite volume when rotating about an axis.
The computational approach to determine the convergence of an improper integral without needing to find the exact limit.
The use of comparison tests to evaluate the convergence of improper integrals involving exponential functions.
The cautionary advice on the dangers of improper integrals of the first kind and the importance of checking for infinite discontinuities.
The summary of the key points and the importance of understanding the nature of improper integrals in mathematical analysis.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: