Lec 37 | MIT 18.01 Single Variable Calculus, Fall 2007
TLDRThis lecture delves into the concepts of improper integrals and infinite series, focusing on their convergence and divergence. The professor introduces improper integrals of the second kind, which have singularities at finite points, and demonstrates how to evaluate them using limits. Examples are provided to illustrate the concept, highlighting the difference between convergent and divergent integrals. The session then transitions to infinite series, emphasizing the geometric series and its convergence criteria. The professor contrasts the behavior of series at infinity with that at finite singularities, using geometric and limit comparison tests to determine convergence. The lecture concludes with a teaser for the next class, where a thought-provoking problem involving stacking blocks will be explored.
Takeaways
- 📚 The lecture continues the discussion on improper integrals, specifically the second kind which have a singularity at a finite point.
- 🔍 The definition of an improper integral of the second kind is given, involving a limit as 'a' approaches 0 from above, and the integral from 'a' to 1 of f(x) dx.
- 📉 The concept of convergence for improper integrals is explained, stating that the integral converges if the limit is finite and diverges if not.
- 🌟 Basic examples of improper integrals are evaluated, such as the integral from 0 to 1 of 1/√x, which converges, and dx/x, which diverges.
- 📚 A general rule for powers is provided: the integral of dx/x^p from 0 to 1 converges when p < 1 and diverges for p ≥ 1.
- 📈 The lecture contrasts the behavior of functions at x approaches 0 and x approaches infinity, highlighting the differences in convergence.
- 📊 The geometric series is introduced as an important and useful infinite series, with its sum calculated as 1/(1-a) when |a| < 1.
- 🔢 Examples of divergent geometric series are given, such as when a = 1 or a = -1, leading to infinite sums or oscillating values.
- 📐 The analogy between certain series and integrals is discussed, with the series 1/n^2 and the integral from 1 to x of dx/x^2 being highlighted as particularly notable.
- 📘 The integral comparison test is introduced as a method to determine the convergence of series by comparing them to integrals.
- 📙 Limit comparison is also introduced as a test to determine if two series have similar convergence properties if their terms tend to 1 as n approaches infinity.
Q & A
What is the main topic discussed in the provided script?
-The main topic discussed in the script is improper integrals, specifically those of the second kind with a singularity at a finite place, and their convergence or divergence.
What is the definition of an improper integral of the second kind as mentioned in the script?
-An improper integral of the second kind is defined as an integral that has a singularity at a finite point. For example, the integral from 0 to 1 of f(x) is defined as the limit as 'a' goes to 0 from above, of the integral from 'a' to 1 of f(x) dx.
How does the professor illustrate the concept of improper integrals with a singularity at a finite point?
-The professor illustrates the concept by imagining a function that comes down towards the x-axis and cuts it off at some point 'a', then lets 'a' approach 0 from the right, observing whether the area under the curve tends to infinity or to some finite limit.
What is the condition for the convergence of an improper integral as discussed in the script?
-The convergence of an improper integral is determined by whether the limit of the integral as 'a' approaches 0 from above is finite. If the limit is finite, the integral converges; if not, it diverges.
Can you provide an example from the script where an improper integral converges?
-An example from the script where an improper integral converges is the integral from 0 to 1 of 1 over the square root of x. The antiderivative is x^(1/2) times 2, and when evaluated at 0 and 1, it yields a finite value of 2.
What is the general rule for the convergence of improper integrals of the form dx / x^p from 0 to 1 as mentioned in the script?
-The general rule mentioned in the script is that the improper integral of the form dx / x^p from 0 to 1 converges when p is less than 1 and diverges for p greater than or equal to 1.
How does the professor contrast the behavior of improper integrals at x=0 and as x approaches infinity?
-The professor contrasts the behavior by pointing out that at x=0, the integral of 1/x^(1/2) is the smallest and the integral of 1/x^2 is very large, whereas as x approaches infinity, the behavior reverses, with 1/x^(1/2) being very small and 1/x^2 being even smaller.
What is the significance of the geometric series in the context of the script?
-The geometric series is highlighted in the script as the most important and useful series, especially when discussing convergence and divergence in the context of infinite series.
According to the script, under what condition does the geometric series converge?
-According to the script, the geometric series converges when the absolute value of the common ratio 'a' is strictly less than 1, which means -1 is strictly less than 'a' and 'a' is less than 1.
Can you explain the Zeno's paradox mentioned in the script and its relation to the geometric series?
-Zeno's paradox, as mentioned in the script, is a philosophical problem that arises from the idea that an infinite number of events can occur in a finite time. In the context of the geometric series, it illustrates the seeming paradox that although the series never actually reaches the sum of 2, the sum of the series is indeed 2 when the common ratio's absolute value is less than 1.
Outlines
📚 Introduction to Improper Integrals of the Second Kind
The professor begins by discussing improper integrals of the second kind, which have a singularity at a finite point. The concept is introduced with the integral from 0 to 1 of f(x), which is defined as the limit of the integral from a to 1 of f(x) dx as a approaches 0 from above. The idea is illustrated with a graphical representation of a function approaching the singularity at point 1. The professor explains the convergence of such integrals, stating that they converge if the limit is finite and diverge otherwise, with examples including the integral of 1 over the square root of x which converges, and the integral of 1 over x which diverges.
📐 Understanding Convergence and Divergence of Improper Integrals
The lecture continues with a deeper exploration of improper integrals, contrasting those with singularities at finite points versus infinity. The professor emphasizes the importance of understanding the behavior of functions as x approaches 0 and infinity, highlighting the differences with examples such as 1/x^(1/2) which is smaller than 1/x and smaller than 1/x^2. The professor illustrates the concept with a graphical representation, showing how the area under the curve can be finite or infinite depending on the function's behavior, and how integrals associated with functions that tend towards infinity or 0 can be divergent.
📉 Analyzing the Behavior of Improper Integrals with Examples
The professor provides a detailed analysis of improper integrals using specific examples, such as the integral of 1/(x-3)^2 from 0 to infinity. The integral is split into two parts to understand its behavior, with the first part being infinite due to the square in the denominator as x approaches 3, and the second part being finite. The conclusion is that while the individual parts may have different properties, the overall integral diverges if it contains an infinite part. The professor also addresses questions from the audience regarding the divergence of improper integrals and the importance of recognizing singularities.
🔍 Transitioning to the Topic of Infinite Series
Moving away from improper integrals, the professor transitions to the topic of infinite series, emphasizing their importance in dealing with infinity. The most important and useful series discussed is the geometric series, introduced through a concrete example. The professor illustrates the convergence of a geometric series to a finite sum using a number line, highlighting the paradox of Zeno's race, which questions the possibility of reaching a point when the number of steps is infinite.
📈 Exploring the Convergence and Divergence of Geometric Series
The professor delves into the general case of geometric series, emphasizing the formula 1/(1-a) for their sum, which only applies when the absolute value of a is less than 1. The lecture contrasts this with cases where a equals 1 or -1, leading to divergence. The professor also touches on the historical and theoretical implications of these series in number theory, where divergent series can sometimes be given meaning under different mathematical frameworks.
🔢 Discussing Series Convergence and Divergence Criteria
The lecture continues with a systematic approach to understanding series convergence and divergence. The professor introduces the notation for partial sums, S_N, and the full limit, S, and explains how the existence of the limit indicates convergence, while its non-existence indicates divergence. The professor also discusses the analogy between series and integrals, using the example of the sum of 1/n^2 from 1 to infinity, which is convergent and can be evaluated, in contrast to the more complex sum of 1/n^3, which is also convergent but more challenging to evaluate.
📚 Establishing the Connection Between Series and Integrals
The professor illustrates the connection between series and integrals using the example of the sum of 1/n from 1 to infinity, which corresponds to the integral from 1 to infinity of dx/x. The lecture demonstrates that the Riemann sum, with delta x equal to 1, can be used to show that the series diverges by comparing it to the integral. The professor also explains the concept of integral comparison and limit comparison tests for determining the convergence or divergence of series.
📘 Applying Comparison Tests to Series
The professor discusses the application of comparison tests to series, providing examples to illustrate how these tests can be used to determine the convergence or divergence of various series. The lecture emphasizes the importance of recognizing the main term in a series and using it to compare with known convergent or divergent series. The professor also teases a demonstration for the next lecture, involving stacking blocks in a specific arrangement, to be explored further.
Mindmap
Keywords
💡Improper Integrals
💡Singularity
💡Convergence
💡Divergence
💡Geometric Series
💡Riemann Sum
💡Limit Comparison Test
💡Integral Comparison
💡Harmonic Series
💡Zeno's Paradox
Highlights
Introduction to improper integrals of the second kind with singularities at finite points.
Definition of improper integrals as a limit process to handle singularities.
Illustration of the concept using a graph to visualize the area under the curve.
Explanation of convergence in improper integrals where the limit results in a finite value.
Evaluation of the integral from 0 to 1 of 1 over the square root of x, demonstrating convergence.
Discussion of the integral of dx / x and its divergence as x approaches 0.
General rule for the convergence of integrals of the form dx / x^p based on the value of p.
Contrasting behavior of functions as x approaches 0 versus infinity for improper integrals.
Visual representation of the balance between convergent and divergent integrals.
Combining concepts of improper integrals with examples involving different types of singularities.
Explanation of the geometric series and its convergence criteria.
The Zeno's paradox and its relation to the concept of infinity in series and integrals.
Introduction to the concept of series, focusing on infinite series and their convergence.
Discussion on the convergence and divergence of series with examples including 1/n^2 and 1/n^3.
Historical note on Euler's calculation of the sum of 1/n^2 as pi^2 / 6.
Comparison of series and integrals to establish a connection between the two.
Demonstration of the Riemann sum and its relation to the series sum 1/n.
Proof of divergence for the series sum 1/n using upper and lower Riemann sums.
Introduction to integral comparison test for determining the convergence of series.
Description of limit comparison test and its application to series convergence.
Examples illustrating the use of limit comparison test for different series.
Engaging problem involving stacking blocks to be addressed in the next lecture.
Transcripts
Browse More Related Video

Calculus Chapter 5 Lecture 50 Infinite Series
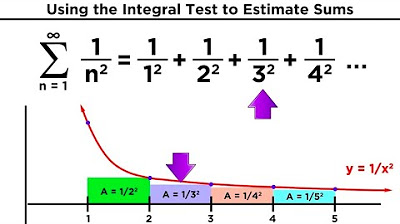
Estimating Sums Using the Integral Test and Comparison Test

Comparison Tests | MIT 18.01SC Single Variable Calculus, Fall 2010

Unit VII: Lec 2 | MIT Calculus Revisited: Single Variable Calculus
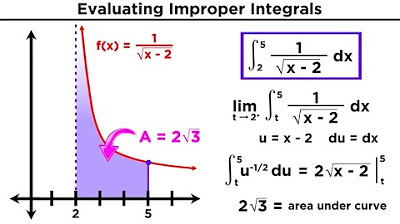
Evaluating Improper Integrals
Calculus Chapter 5 Lecture 53 Absolute & Conditional
5.0 / 5 (0 votes)
Thanks for rating: