Alternating Series

RH Mathematics
14 Feb 202410:01
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video delves into the concept of alternating series, characterized by terms that alternate in sign. It explains how to determine the convergence of such series, particularly in geometric settings with a negative ratio, using the formula involving the first term and the ratio. The video also covers the alternating harmonic series, demonstrating its convergence through partial sums and the application of the alternating series test. Examples include series involving cosine functions and their convergence properties, emphasizing the importance of the series' terms decreasing in magnitude to zero for convergence.

Takeaways
  • πŸ” The video discusses alternating series, which are series where terms alternate in sign, such as + - + - + -.
  • πŸ“š An example of an alternating series is given as 18 - 12 + 8 - 16/3 + 32/9, which is geometric with a negative ratio.
  • πŸ“‰ The video explains that if the absolute value of the ratio of consecutive terms is less than one, the series converges.
  • πŸ”’ A formula for the sum of a convergent alternating series is provided: first term times one over (1 - ratio).
  • πŸ“ The video introduces summation notation for alternating series and explains the use of exponent properties in series.
  • 🌐 The concept of series alternating due to negative one to the power of n (-1^n) or cosine of pi times n is discussed.
  • πŸ“‰ The function f(x) involving cosine of nx over the square root of n is explored, showing how it forms an alternating series for certain values of x.
  • πŸ“Š The alternating harmonic series is shown to converge, contrary to the non-alternating harmonic series which diverges.
  • πŸ“ˆ The video demonstrates the convergence of the alternating harmonic series by computing partial sums and using Desmos to visualize the convergence to a finite value.
  • πŸ“š The Alternating Series Test is introduced as a method to determine the convergence of an alternating series with decreasing magnitude terms.
  • 🚫 The video clarifies that the Alternating Series Test cannot be used to prove divergence, only convergence.
Q & A

  • What is an alternating series?

    -An alternating series is a type of series where the terms alternate in sign, typically represented as a sequence of positive and negative terms such as + - + - + -.

  • How does the sign of the terms in an alternating series affect its convergence?

    -The sign of the terms in an alternating series is crucial for its convergence. If the absolute value of the ratio of consecutive terms is less than one, the series is likely to converge, as the alternating signs help to reduce the magnitude of the terms.

  • What is the formula to find the sum of an alternating geometric series?

    -The sum of an alternating geometric series can be found using the formula: first term times one over (1 - ratio), where the ratio is the common ratio of the geometric series.

  • What is the significance of the ratio in an alternating geometric series?

    -The ratio in an alternating geometric series is significant because if its absolute value is less than one, it indicates that the series is likely to converge.

  • How can the property of exponents be applied to the terms of an alternating series?

    -The property of exponents can be applied to distribute the power over a product, which is useful in simplifying the terms of an alternating series, especially when dealing with geometric progressions.

  • What causes a series to alternate in terms of mathematical functions?

    -A series can alternate due to factors such as (-1)^n or cosine of Ο€ times n, which introduce a periodic change in sign for each term in the series.

  • Why is the cosine function used to demonstrate the alternating property in series?

    -The cosine function is used because it has a periodic nature, with values oscillating between -1 and 1, which clearly demonstrates the alternating property when multiplied by the terms of a series.

  • What is the alternating harmonic series, and does it converge or diverge?

    -The alternating harmonic series is the alternating version of the harmonic series, represented as 1 - 1/2 + 1/3 - 1/4 + ... It converges, contrary to the non-alternating harmonic series which diverges.

  • How can partial sums be used to determine the convergence of a series?

    -Partial sums can be used to determine the convergence of a series by observing if the sum of a finite number of terms approaches a finite limit as more terms are added. If the limit exists, the series converges.

  • What is the Alternating Series Test, and how is it applied?

    -The Alternating Series Test is a method to determine the convergence of an alternating series. It states that if the terms are decreasing in magnitude and approach zero, the series converges. It is applied by checking these two conditions for the given series.

  • Why can't the Alternating Series Test be used to show divergence?

    -The Alternating Series Test can't be used to show divergence because it is specifically designed to test for convergence. It does not provide any information about the behavior of a series if it does not meet the conditions for convergence.

Outlines
00:00
πŸ“š Introduction to Alternating Series

This paragraph introduces the concept of alternating series, which are series with terms that alternate in sign, such as +1 -2 +3 -4, etc. The video script discusses a specific type of alternating series found in a geometric setting with a negative ratio, exemplified by the series 18 - 12 + 8 - 16 + 32/9, and so on. The script explains that if the absolute value of the ratio is less than one, the series converges. It also introduces a formula to find the sum of a converging alternating series, which involves the first term and the ratio. The paragraph further explains the role of the negative ratio in causing the terms to alternate and introduces summation notation for such series. It also touches on the properties of exponents and how they relate to the series, and mentions two common causes for a series to alternate: the negative one to the power of N and cosine of pi times N.

05:03
πŸ“ˆ Exploring Series Convergence and the Alternating Series Test

The second paragraph delves into the convergence of alternating series, using technology to compute partial sums of the series and observing the pattern of convergence. The script uses Desmos, a graphing calculator, to demonstrate the convergence of the alternating harmonic series, which is the alternating version of the harmonic series. It shows that the series does not diverge as the harmonic series does, but instead converges to a finite value. The script then introduces the Alternating Series Test, which states that if an alternating sequence's terms decrease in magnitude to zero, the series converges. The test is applied to the function f(x) involving cosine of NX over the square root of N, determining whether it converges for x equals 0 and x equals pi. The script clarifies that the Alternating Series Test can only confirm convergence, not divergence, and concludes by discussing the limitations of the test and its proper application in AP Calculus.

Mindmap
Keywords
πŸ’‘Alternating Series
An alternating series is a type of series where the terms alternate in sign, typically represented by a sequence of positive and negative terms such as '+ - + - + -'. In the video, the concept is central as it discusses the properties and tests for convergence of such series. An example given in the script is the series '18 - 12 + 8 - 16 + 32/9 - ...', which is geometric and converges due to the absolute value of its ratio being less than one.
πŸ’‘Convergence
Convergence in the context of series refers to the property where the sum of an infinite sequence approaches a finite value. The video explains that if the absolute value of the ratio of successive terms in an alternating series is less than one, the series is likely to converge. This is demonstrated with the geometric series mentioned, which converges because the terms are getting smaller and the sign alternates.
πŸ’‘Geometric Series
A geometric series is a series where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. In the video, the script describes a geometric series with a negative common ratio, which leads to an alternating series that converges. The formula to find the sum of a convergent geometric series is also discussed.
πŸ’‘Summation Notation
Summation notation is a compact way of writing long sums, represented by the Greek letter 'Ξ£'. The video script uses this notation to express the general form of an alternating geometric series, indicating the starting term, the common ratio, and the pattern of alternation using '-2^(3) to the power of n'.
πŸ’‘Exponent Property
The exponent property mentioned in the video refers to the mathematical rule that allows the power of a product to be distributed as the product of the powers. The script uses this property to simplify the expression of the alternating geometric series, breaking down '-2/3' into '-1 * 2/3' to illustrate how the alternation occurs.
πŸ’‘Cosine Function
The cosine function is a periodic function that is used in the video to create an alternating series through the expression 'cosine of pi times n'. The video explains how the cosine function's values alternate between 1 and -1 as 'n' changes, contributing to the alternation of the series' terms.
πŸ’‘Power Series
A power series is an infinite series where the terms are powers of a variable. In the video, a function 'f' is defined by a power series involving the cosine function and the square root of 'n'. The video discusses the convergence of this series for different values of 'x', such as 0 and pi.
πŸ’‘Harmonic Series
The harmonic series is the sum of reciprocals of the natural numbers, which is known to diverge. The video introduces the alternating harmonic series, where the signs of the terms are alternated, and demonstrates that this version of the series converges, contrary to the non-alternating harmonic series.
πŸ’‘Partial Sums
Partial sums are the sums of the first 'n' terms of an infinite series. The video script uses partial sums to illustrate the convergence of the alternating harmonic series, showing that as more terms are added, the sum approaches a finite value.
πŸ’‘Natural Logarithm
The natural logarithm is a logarithm to the base 'e', where 'e' is an irrational number approximately equal to 2.71828. In the video, the script uses the natural logarithm of 2 to demonstrate the limit to which the alternating harmonic series converges, providing a visual aid for understanding convergence.
πŸ’‘Alternating Series Test
The alternating series test is a method to determine the convergence of an alternating series. The video explains the test by stating that if the terms of an alternating series decrease in magnitude to zero, then the series converges. This test is applied to the series involving the cosine function to confirm its convergence.
Highlights

Introduction to alternating series with terms that alternate in sign, such as + - + - + -.

Geometric series with a negative ratio as an example of an alternating series.

The importance of the absolute value of the ratio being less than one for convergence.

Formula for finding the total of a converging series: first term times one over (one minus the ratio).

Explanation of the role of the negative ratio in causing the series to alternate.

Summation notation for an alternating series and the exponent property of products.

The role of -1^N and cosine of Ο€N in causing a series to alternate.

Demonstration of the alternating nature of cosine of Ο€N with different values of N.

Writing the terms of a function defined by a power series with cosine of NX over the square root of N.

Difference between F(0) not being an alternating series and F(Ο€) being one.

Introduction to the alternating harmonic series and its convergence.

Computing partial sums of the alternating harmonic series to demonstrate convergence.

Use of Desmos to visualize the convergence of the alternating harmonic series.

The Alternating Series Test theorem and its conditions for a series to converge.

Application of the Alternating Series Test to determine the convergence of F(x) when x equals 0 and Ο€.

Clarification that the Alternating Series Test cannot be used to show divergence.

Conclusion of the video with a summary of the Alternating Series Test and its implications.

Transcripts

Browse More Related Video

Calculus BC – 10.7 Alternating Series Test for Convergence

Alternating Series, Types of Convergence, and the Ratio Test

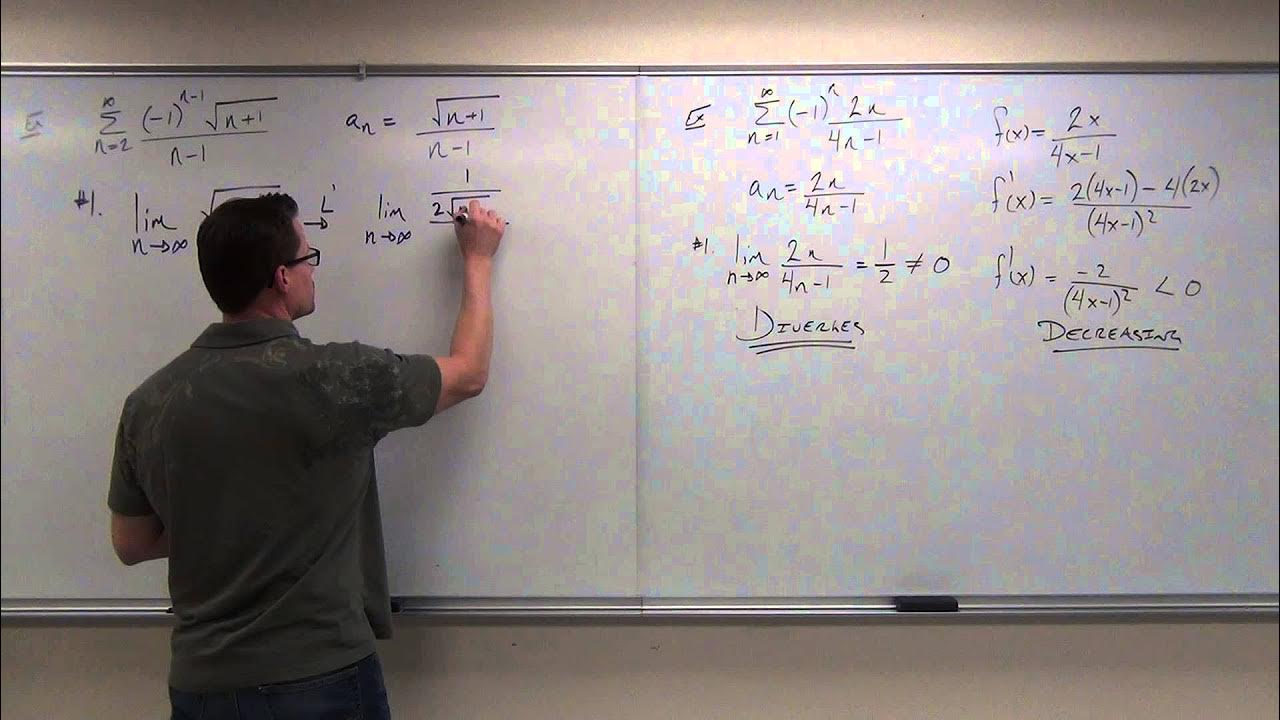
Calculus 2 Lecture 9.5: Showing Convergence With the Alternating Series Test, Finding Error of Sums

A Lot of Series Test Practice Problems

Alternating Series Test and Error for Alternating Series

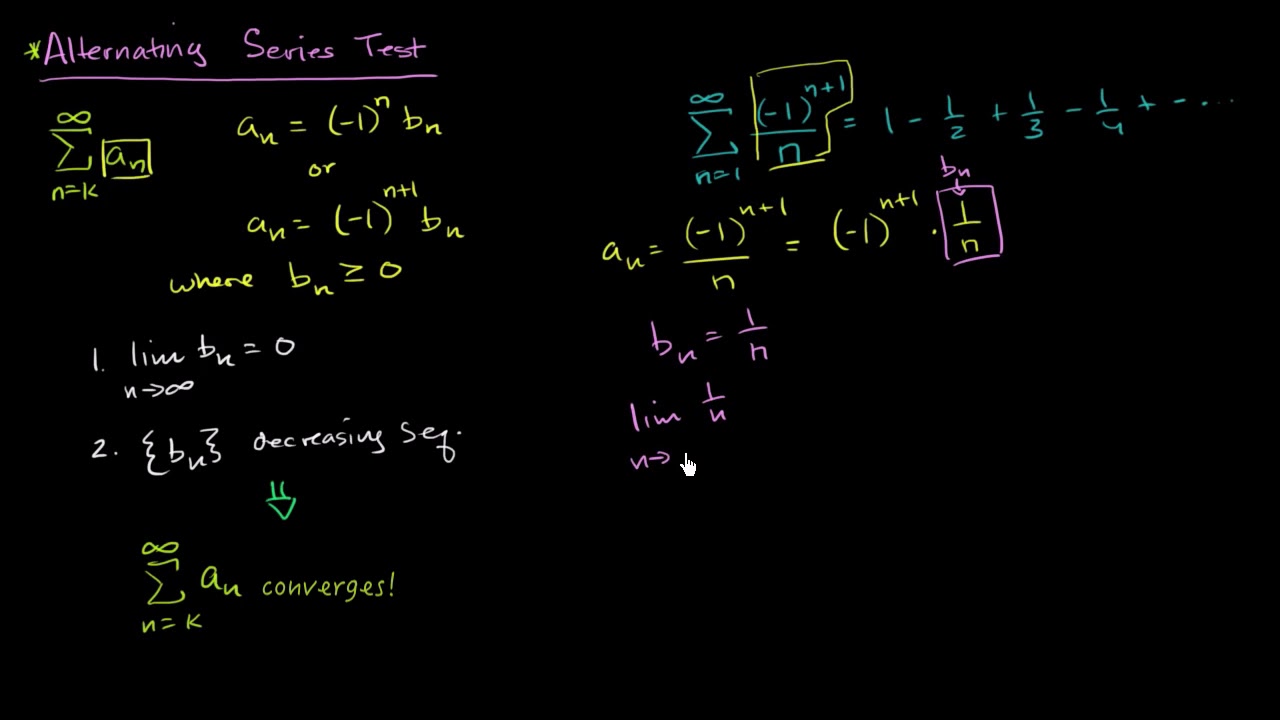
Alternating series test | Series | AP Calculus BC | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Alternating SeriesConvergence TestGeometric SeriesHarmonic SeriesMathematicsCalculusEducationalSeries AnalysisCosine FunctionSummation Notation